你是否也经历过这些烦恼：正准备出门，却发现忘了给手机充电；或者正在路上，突然想起电动汽车需要充电。固态电池一旦应用于电动汽车、电子设备和储能系统，诸如此类的问题将彻底成为历史。固态电池不仅有望实现充电更快、续航更长，还具备更高的安全性。仿真技术能够帮助电池设计师深入研究固态电池，更准确地预测其在未来应用中的性能表现。

固态电池：一项备受期待的技术

固态电池（Solid-state batteries，SSB）采用固态电解质在电极间传导离子，而传统电池则使用液态电解质或凝胶聚合物。这种差异使得固态电池相较于锂离子电池具备诸多优势，例如更长的使用寿命。当前电动汽车电池的使用寿命通常为 5–8 年，而固态电池可将寿命延长至 15–20 年。此外，常规的锂离子电池在 1000 次充放电后性能衰减明显，固态电池则能在 5000 次充放电循环后仍保持 90% 的初始容量（参考文献 1）。

固态电池应用于电动汽车意味着更短的充电等待时间。照片来自 Haberdoedas， 发布在 Unsplash.

固态电池的充电速度也远超其他类型的电池。普通锂离子电池充电至 80% 的电量大约需要 45 分钟，而固态电池充电到相同电量仅需 12 分钟，甚至最短只需 3 分钟。固态电池的安全性也更高——由于不含液态电解质，其可燃性和挥发性远低于其他电池。此外，通过避免使用液态电解质和碳阳极，它们还能提供更高的能量存储密度（参考文献 1）。

跨越数十年的设计挑战

固态电解质最早是由物理学家迈克尔·法拉第于19 世纪 30 年代初发现的，其工作原理与潜在应用从那时起就成为研究焦点。时间快进至21世纪20年代，众多汽车制造商、电子企业和研究机构正将大量研发资源投入到固态电池领域。然而，电池的研究和设计是一个成本高昂且资源密集的过程，仿真技术可协助开发者研究和探索在不同工况和应用场景下的设计难题。

固态电池会受到 锂化 现象的影响，在这一过程中，电池固态组件内的电极会发生膨胀和收缩，从而产生机械应力。此外，在充放电过程中电池内部离子的迁移同样会导致应力与体积变化。这些问题可能会缩短电池寿命、降低储能效率，甚至导致机械故障。

多物理场建模和仿真可用于分析固态电池的设计。在固态电芯的异构模型教程模型中，我们将带您了解在 COMSOL Multiphysics^® 软件中的建模过程。

在 COMSOL Multiphysics® 中模拟固态电池

固态电芯异质模型的教程模型模拟了固态电池的充放电循环，重点研究了电荷和质量传输与固体力学之间的相互作用。该模型的几何结构由复合正极、锂金属负极以及位于两个电极之间的固态电解质隔膜组成。

固态电池模型的几何结构。

软件中内置的专用物理场接口与功能使模型设置简单直观。通过 锂离子电池，固体传递, 以及 固体力学 接口，可分别实现电荷守恒、质量守恒与动量守恒的建模。此外，软件还提供专门的功能用于模拟：

• 负极金属锂的沉积与溶解
• 正极的膨胀与收缩
• 电极-固态电解质界面处的氧化还原反应

COMSOL Multiphysics^® 中的固态电池模型与物理场的设置。

异质固态电池的模拟对充电结束时的若干物理量进行了评估，包括固态电解质中的电势、离子电势及 von Mises 应力。

固态电解质中的电势（左）、正极浓度（中）以及应力（右）。

模拟结果还包括对全局量的评估，包括电池电压、充电状态以及 z 方向的应力。

为固态电池的发展铺平道路

借助仿真技术研究固态电池的力学特性，可帮助研究人员、汽车制造商及电子企业在未来几年（而非几十年）将固态电池整合到零部件与设备中。

点击下方按钮，亲自动手尝试固态电芯异质模型的建模与仿真。我们也建议您为电池仿真配备以下 COMSOL Multiphysics^® 附加产品：电池模块、CAD导入模块、结构力学模块以及非线性结构材料模块。

扩展阅读

• 模拟电化学阻抗谱中的非理想行为
• 电池组热蔓延仿真
• 如何在电池模型中定义载荷循环

参考文献

1. Shang et al., “A comprehensive review of solid-state lithium batteries: Fast Charging characteristics and in-operando diagnostics,” Nano Energy, vol. 142, part B, 2025. Doi: 10.1016/j.nanoen.2025.111232

随着锂离子电池的老化，寄生反应会影响电解液中溶剂的比例。这篇博客，我们将探讨单一溶剂的消耗如何影响电池的长期性能。

双重尺度建模

锂离子电池中的液态电解质通常由锂盐（如 LiPF₆）溶解于一种或多种碳氢基溶剂中构成，并含有其他添加剂。对于含有多种溶剂的电解液，隔膜和电极内的传递属性不仅取决于盐的浓度，还与溶剂的比例密切相关。

随着电池老化，固态电解质界面的形成等寄生反应会选择性消耗特定溶剂，导致溶剂比例随时间变化。这种动态变化将影响电解液传递属性与局部盐浓度的关系，进而作用于电池全生命周期性能。

为了解单一溶剂消耗对电池性能的影响，我们采用双尺度建模的方法。首先，我们使用 Compular Lab（Compular 的一个网络应用程序）中提供的分子动力学（MD）功能，精确计算电解液的传递属性。然后，将 Compular Lab 计算结果导入 COMSOL Multiphysics^® 软件中的 锂离子电池 接口。该接口采用了一个电池尺度的模型，即 Doyle–Fuller–Newman 锂离子电池模型的扩展版本，来加深我们的理解。具体来说，我们对原始模型进行了扩充，在负极中考虑了固体电解质界面（SEI 膜）生长的过程，该过程会消耗电解液中的溶剂。SEI 膜的增长是一种公认的锂离子电池老化机制。

传递属性

电池尺度模型定义了隔膜和多孔电极（正极和负极）中孔隙电解质的电流、电荷和物质（特别是盐）的平衡。同时，它还定义了这些多孔电极内发生的电化学电荷转移反应及其电子传导中的电流平衡。

隔膜和孔隙电解质中的电流和物质平衡方程（参考文献 1）包含依赖于电解质溶液中溶剂的传递属性。这些特性由4个模型参数决定：

• 电解质电导率,
• 扩散系数,
• 传递数,
• 热力学因子, , 其中 表示活度系数， 表示盐浓度

下式为电解质电流密度矢量 () 的表达式，用于描述电解质的电流平衡。它说明了电解质电导率、传递数和热力学因子参数如何影响离子的迁移和扩散：

1

下式描述了盐的通量 (),并将其纳入相应的物质平衡中。这里，盐的扩散系数和传递数会影响扩散和迁移对盐离子移动的贡献：

2

上述方程中， 表示离子电势（因变量）， 表示无量纲盐浓度（也是因变量）。 和 分别表示法拉第常数和通用气体常数。 表示温度，温度可以是一个因变量，但在本例中保持不变。

控制传递属性的 4 个模型参数值取决于溶液的成分。在我们的模型中，我们探讨了碳酸乙烯酯（EC）和碳酸甲乙酯（EMC）的混合溶剂，EC:EMC 的初始比例为 3:7。这些模型参数是通过 Compular Lab 中的分子动力学（MD）模拟，针对不同盐浓度和溶剂浓度进行计算得出的。

分子动力学模拟从第一原理出发预测电解质的特性，主要是对原子和分子组成的大体系求解牛顿运动方程。这一过程会产生大量关于单个原子如何运动的数据，随后对这些数据进行分析，进而提取如密度、黏度等材料特性，以及对电解质至关重要的离子传递属性。原子间的相互作用由经典物理方程控制，而不同作用力的强度参数源自量子化学计算。通过这些计算，我们可以根据对基础物理学的理解来预测原子和分子特性。因此，分子动力学模拟可应用于任何配方体系，甚至是尚未合成过的化学物质。Compular Lab 允许用户指定要模拟的电解质，并自动进行分子动力学模拟。

在以下模拟中，我们根据 Compular Lab 分子动力学模拟生成的数据拟合了基于物理机理的半经验多项式曲线，这些数据在不同的盐浓度和 EC:EMC 比例下各不相同。因此，前文所述的4个模型参数被转化为盐浓度和溶剂成分的函数。然后，我们将这些函数输入 COMSOL 模型。

下图 1 显示了不同 EC:EMC 比例下电解质电导率 与盐浓度 () 的多项式表达式，以百分比表示。值得注意的是，30% 的值对应于 3:7 的初始比例。

图 1. 使用 Compular Lab 计算的 5 种不同 EC:EMC 比例下电解质电导率与盐浓度的函数关系。

如图 1 所示，当离子浓度较低时，由于离子电流所需的电荷载流子数量不足，电解质电导率最初较低。随着盐浓度的增加，电解质电导率达到最大值。当盐浓度较高时，电解质电导率下降，这一变化可归因于离子迁移率降低。这种效应也反映在下面的扩散系数曲线中。

图 2.使用 Compular Lab 计算的 5 种不同 EC:EMC 比例下的盐扩散系数与盐浓度的函数关系。

图 2 显示了盐的扩散系数与盐浓度的函数关系。曲线显示，扩散系数随着盐浓度的增加而降低，这种趋势可归因于盐离子之间的“摩擦力”增强导致离子流动性降低。此外，曲线还显示，扩散系数随着 EC 的增加而降低。由于 EC 比 EMC 具有更高的黏度，这表明溶剂与溶剂之间的相互作用力更大，这也会降低离子的流动性，增加离子在溶剂中的“摩擦力”。

与直觉相反的是，在大部分盐浓度范围内，电解质电导率随着 EC 含量的增加而增加（见图 1），而在整个盐浓度范围内，EC 含量越高，扩散系数越低。这种现象源于 EC 的溶解能力较强，导致离子对和聚集体较少，并说明了浓缩二元电解质中电导率和扩散率之间的复杂关系。

正离子的传递数，即正离子携带的离子电流比例，并没有随着盐浓度的变化而呈现出明确的趋势，也没有因溶剂成分的不同而表现出显著的差异。在本研究中，我们计算了一个平均传递数 ，该传递数在所有盐浓度和 EC:EMC 比例下均一致。

下图 3 显示，热力学因子似乎与溶剂比例无关。从图中可以看出，活性系数 与盐浓度呈线性关系。应用关系式 ，得到的实线代表图中所有 EC:EMC 比例下的热力学因子。

图 3. 热力学因子与盐浓度的函数关系，似乎与 EC:EMC 比例无关。

固体电解质界面

固体电解质界面（SEI）在锂离子电池的负极生长是一种公认的老化机制。在我们的模型中，我们假定 SEI 的形成反应根据以下电化学反应消耗 EC：

3

将 Tafel 表达式与 EC 通过 SEI 传递时的极限电流相结合来描述该反应的动力学原理（参考文献 2）：

4

上式中， 表示 SEI 形成的局部电流密度， 表示 EC 耗尽导致的极限电流密度， 表示参考状态下的盐浓度， 表示同一参考状态下的交换电流密度。过电位用 表示， 代表 Tafel 斜率。

极限电流密度可通过 SEI 厚度用下式估算得出：

5

式中， 表示 EC 的摩尔分数， 是 SEI 厚度为 时的极限电流密度， 表示当前的 SEI 厚度。

为了跟踪 SEI 的生长过程，我们根据法拉第定律和上述电化学反应动力学建立了一个物质平衡方程。由于 SEI 保持在其形成的位置（即没有 SEI 通量），其物质平衡由分布式常微分方程表示，适用于电极内的每个点（每个 x、y 和 z 坐标）：

6

式中， 表示 SEI 的浓度， 表示比表面积。

SEI 的厚度由以下公式计算

7

式中， 表示 SEI 的摩尔体积。

通过对整个电极的 SEI 浓度进行积分，可得出任意给定时间内的 EC 总量， ：

8

因此，溶剂中 EC 的摩尔分数为

9

该表达式用于计算上文所述的极限电流密度。

孔隙率和有效传递属性

随着电池老化，SEI 层的形成会降低孔隙电解质的孔隙率，从而改变有效传递属性。任何给定时间的电解质体积分数（）都可以用下式计算：

10

然后，利用 Bruggeman 关系计算孔隙电解质中的有效扩散率和电导率：

11

在 COMSOL Multiphysics^® 中模拟

上述方程在 COMSOL Multiphysics^® 的附加产品电池模块中的 锂离子电池 接口中已定预定义，最大限度地减少了用户界面（UI）中所需的手动调整。为了加入沉积物质，我们指定了一个 SEI 浓度变量及其密度和摩尔质量。此外，还在负多孔电极特征中添加了多孔电极反应。该反应特征中定义了电化学反应的化学计量，选择 Tafel 方程，并输入了极限电流密度。下图 4 展示了该配置在用户接口中的显示。

图 4. COMSOL Multiphysics 用户界面截图，锂离子电池 接口和 多孔电极 特征中定义的 SEI 反应。

有和没有溶剂依赖属性的结果

电池在 1C 放电速率下的健康状态（SOH）（恒定电流下 1 小时内电池完全放电）清楚地表明了依赖溶剂的传递属性的影响。图 5 比较了两种情况下 1C 放电循环计算出的SOH：一种情况是考虑了依赖溶剂的传递属性，另一种情况是这些属性保持不变。图 5 中可能具有实际意义的一点是，当考虑到传递属性的变化时，与不考虑这些变化的情况相比，模型预测要达到 0.9 SOH 需多进行约 200 次循环。

图 5. 溶剂依赖和与溶剂无关的传递属性在 1C 时的相对放电能力。

图 6 显示了与图 5 模拟相对应的 EC:EMC 比例。从图中可以看出，两种方案的结果完全相同。EC:EMC 比例从初始状态的 30% 下降到 1400 个周期后的 2% 以下。

图 6. EC:EMC 比例与 1C 循环次数的关系。

由于溶剂的消耗，盐浓度随着循环次数的增加而增加。图 7 描述了电池中的盐浓度与循环次数的函数关系。这当然会对传递属性产生影响；不过，两种情况下盐浓度的增加是相同的。

图 7. 图 5 中两种情况下电池中的盐浓度与 1C 下循环次数的关系。

一个有趣的问题是，在考虑和不考虑溶剂组成对传递属性影响的两种情况下，电池性能如何变化。图 8 展示了两种情况下电池在 100% SOH 和 90% SOH 条件下的放电曲线。

图 8. 图 5 中两种情况下电池在 100% 和 90% SOH 条件下的放电曲线。

图 8 表明，考虑了 EC:EMC 比例变化对传递属性影响的模型，在 SOH 为 90% 状态下预测的 1C 倍率容量略高。图 9 显示了两种情况下的总极化，表明考虑了溶剂属性的情况下，SOH 为 90% 时的极化较低，从放电状态 (SOD) 为 0.4 开始，到 SOD 为 0.8 以上时达到最大差异。

图 9. 图 5 中 100% SOH 和 90% SOH 两种情况下的极化。

在考虑传递属性时，观察到的性能提升虽然不大，但具有重要意义——在 0.8 SOD 时约为 40 mV 的改善。这种改善可归因于低 EC 含量时较高的扩散系数。图 10 进一步说明了这一点，它显示了两种方案在 90% SOH 条件下放电结束时（约 0.9 SOD）的盐浓度，并清楚地表明，该模型考虑了溶剂中不同的传递属性，使盐浓度更加均匀。反过来，这又增强了电导率，降低了浓度过电位。

图 10. 上图 5 中两种情况下，在 SOH 值为 90% 时，放电结束时（0.9 SOD）的盐浓度。

分子动力学和电池模型联用以提高预测精度

我们使用了两种模型模拟锂离子电池的老化效应：一种模型考虑了老化过程中溶剂成分变化（EC:EMC）带来的传递属性变化，另一种模型则不考虑传递属性的变化。此外，还使用 Compular Lab 计算了传递属性与溶剂成分和盐浓度的关系。

模拟结果表明，溶剂成分对传递属性的影响有限但意义显著，在 0.8 SOD 和 90% SOH 条件下，极化差值约为 40 mV。更重要的是，在考虑了属性变化的情况下，预测电池在达到 90% SOH 之前可多循环 200 次。

上述模型展示了如何在 COMSOL Multiphysics^® 和 Compular Lab 中进行这类仿真研究。需说明的是，虽包含所有研究要素，但本研究并非完整的科研项目，旨在说明两个软件平台的原理和使用方法。

下一步

• 想尝试模拟上述模型吗？在 COMSOL 案例库中下载相关的 MPH 文件：
  • 锂离子电池老化与不同溶剂组分的影响
• 有兴趣进一步了解如何使用 Compular Lab 生成参数吗？请查看 Compular 网站上的这篇博客：
  • 如何模拟溶剂分解对电池性能的影响？

参考文献

1. Doyle, J. Newman, A.S. Gozdz, C.N. Schmutz, and J.M. Tarascon, “Comparison of Modeling Predictions with Experimental Data from Plastic Lithium Ion Cells,” J. Electrochem. Soc., vol. 143, no. 6, pp. 1890–1903, 1996.
2. Ekström and G. Lindbergh “A model for predicting capacity fade due to SEI formation in a commercial Graphite/LiFePO4 cell”, J. Electrochem. Soc., vol. 162, pp. A1003–A1007, 2015.

设想一个场景：一个电池组连接到充电器上正在充电。第 1 分钟，一切正常，电能正常流入电池组。突然，一个电池单元发生短路并迅速升温，进而引发连锁反应，电池组中的其他电池纷纷效仿。20 分钟后，整个电池组已经完全损坏。为了研究这种存在安全隐患的情况，我们模拟了一个经历这种快速变化过程的电池组。

电池出问题的风险

当电池超出其正常工作范围、受到损坏或发生短路时，就会像上述例子一样出现热失控。在这个过程中，电池会不受控制地升温，并引发邻近的电池也跟着升温。如果没有足够的散热来抵消过多的热量，整块电池就会出现热失控。这会迅速损坏整个电池组，使其无法使用。最坏的情况下，极端高温甚至会引发火灾，造成极其严重的后果。

如果电池设计或操作不当，极易发生热失控事件。照片由 Roberto Sorin 拍摄，通过 Unsplash共享。

要深入探究这类故障在未来电池设计中的发展和演变，电池设计人员可以借助建模与仿真来测试他们的设计，从而避免在此过程中损坏任何材料或造成人员伤害。通过仿真，他们能够仔细地查看电池组内部（这在实验室中无法实现），尤其是 多物理场 仿真模型，能够正确反映电池组在真实工作环境中的运行状况。

在 COMSOL Multiphysics^® 中建立电池组模型

以一个由20 个圆柱形电池组成的5s4p 配置的简单电池组为例。在 5s4p 配置中，4 组电池单元并联，每组包含 5 个串联的单个电池。在这个示例模型中，我们添加了两个塑料支架，用于将电池保持在各自的位置以及固定电池与电池之间的距离。模型还包括焊接在串行连接器上的并行连接器（位于电池圆筒中间），以及包裹整个电池组的一层薄塑料包装。包裹层在电池圆筒周围形成了一个静态气室。

电池组的几何模型。

该模型使用了 COMSOL Multiphysics^® 软件材料库中的以下材料：

• 丙烯酸塑料（用于塑料支架）
• AISI 4340 钢（用于连接器和电池端子）
• 空气（用于气室内的空气）

接下来，让我们触发电池组的热失控！为了启动热失控蔓延，假设在充电过程的早期一个电池发生短路。。

热失控模拟

在我们的模拟中，一旦短路被触发（充电 1 分钟时），电池组内的最高测量温度瞬间升高超过 300 °C。然而，由于只有一个电池经历了这种温度的急剧上升，电池组的平均温度仅有轻微的上升。我们观察到一个潜伏期，在此期间，邻近的电池被问题电池加热，直到另一个电池被触发瞬间升温。

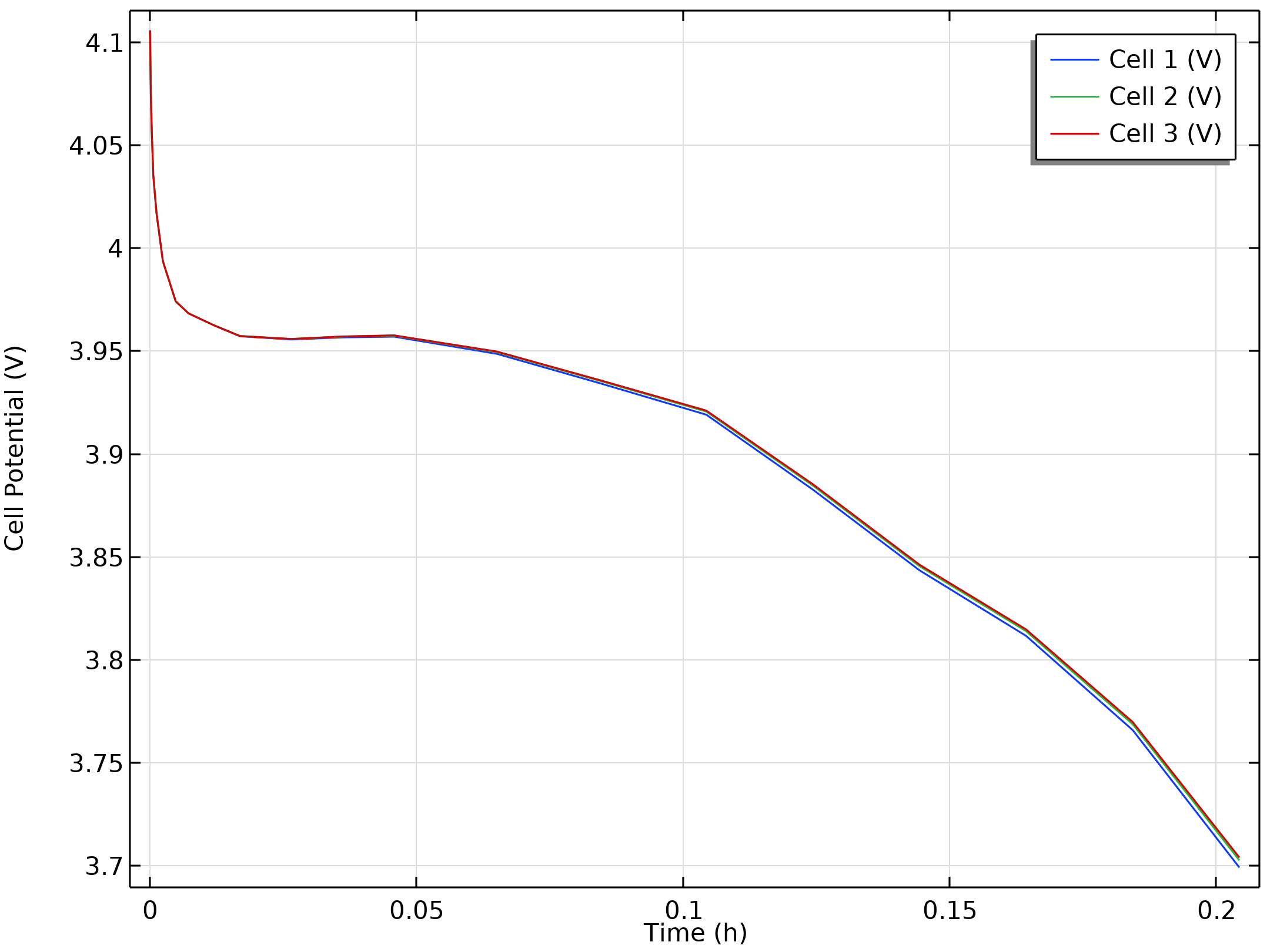
电池组中的电压和最高温度。

其余电池触发热事件的临界温度为 80°C，随着电池组整体热量的增加，电池相继失控的时间间隔变得更短。为了模拟电解质的流失和由此导致的电池内部电阻增加，在触发热事件时，电池的内部欧姆电阻被设定为增加约两个数量级。

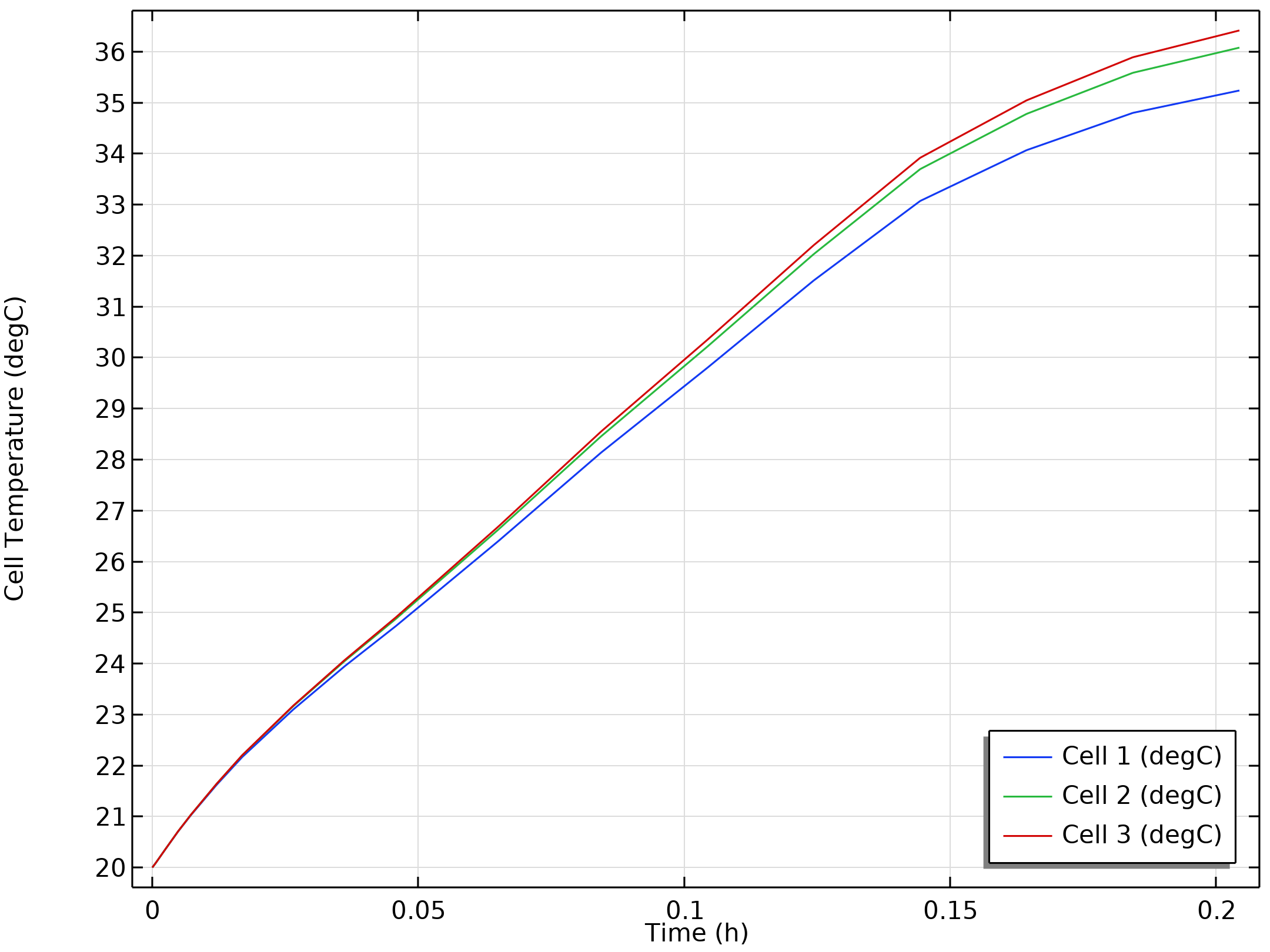
电池组内电池温度随时间的变化情况。

在第 10 分钟时，已经达到最大充电电压限制，充电器关闭。但这时已经太晚了，无法阻止电池的进一步损坏，热失控继续蔓延到电池组的其他部分。短短几分钟后， 20 个电池全部损坏。到 20 分钟时，热失控过程已经结束，但电池组的平均温度仍然在 350°C 以上。如果这是一个真实的电池组，模拟的场景很可能会导致火灾，甚至爆炸。

防患于未然

电池长时间处于高温状态、以不安全的方式运行或者受损，都可能引发热失控事件。当系统的某个部分开始过热时，情况就会迅速恶化。通过模拟这些事件，用户可以在虚拟环境中测试电池设计，并验证电池热管理系统的有效性，以及在潜在部署位置的系统温度调节能力等。通过多物理场仿真方法，电池设计人员可以更深入地理解热失控事件，并有望完全避免这种情况发生。

想自己动手尝试模拟吗？点击下方按钮，进入COMSOL案例库，下载相关模型文件。

扩展资源

• 阅读 COMSOL 博客，了解有关电池仿真的更多信息:
  • 锂离子电池组中的热分布分析
  • 如何延长锂离子电池的使用寿命
  • 数字孪生模型和基于模型的电池设计
• 观看关于如何设计高性能、耐用和安全的电池的演示

当模拟一个电池系统时，指定载荷曲线对于准确反映电池在实际应用中的运行情况至关重要。 COMSOL Multiphysics^® 软件和电池模块中提供了多种方法，用于在电池模型中定义各种载荷曲线。这篇博客，我们将对这些方法进行讨论，并详细介绍如何实现。为了演示如何使用这些方法，我们来看几个COMSOL Multiphysics^® 案例库中的模型示例。

简介

在 COMSOL^® 软件中，通常通过定义和指定外加载荷来完成电池模型的构建，外加载荷可能是电流、功率、电压或这些变量的组合。根据在模型中使用的电池接口，你可以选择合适的边界条件或运行模式，并设置相关值来满足要模拟电池的运行要求。

例如，锂离子电池，二元电解质电池 和 铅酸电池 接口提供了各种电极条件选择，用于模拟一般电流分布。另外，在像 单颗粒电池 和 集总电池 这样的简化电池接口中，可以选择一种运行模式。对于电池组尺度，可以在 电池组 接口，通过设置电池组内的 电流导体 域的边界条件来指定载荷。

COMSOL Multiphysics^® 和电池模块提供了多种方法，可用于表征分布持续时间、变化和循环模式，并将它们集成到你创建的表达式中，然后将这些信息作为外加载荷传递到物理场接口。在接下来的章节中，我们将讨论这些方法。

充放电循环期间风冷圆柱形锂离子电池的温度分布。

函数

在 COMSOL Multiphysics^® 中，我们可以选择不同的函数来定义各种载荷曲线。利用这些函数，可以精确表征包括随时间变化的模式和变量在内的载荷曲线特征。还可以将这些函数集成到表示载荷的表达式中，例如电池模型中使用的外加电流。在锂离子电池等温模型：一维教学案例中，用于产生恒定电流充放电循环的外加电流以及静置期，都是使用 分段 函数定义的。该函数尤其适用于定义在已知时间间隔内变化的载荷。

同样，在锌-氧化银电池等温模型：一维教学案例中，采用了 分段 函数来定义放电电流密度脉冲分布。在圆柱形锂离子电池热建模：二维和圆柱形锂离子电池热建模：三维教学案例中，采用了 波形 函数来建立交替的充放电电流以及弛豫过程。在 可溶性铅酸氧化还原液流电池教学案例中，采用了三个 矩形 函数定义由充电、放电和静置过程组成的载荷循环。根据输入和对所需载荷循环的了解，我们可以使用一个或多个函数和（或）不同类型的多个函数的组合来实现所需的分布。

载荷曲线的突然变化或不连续会导致数值不稳定。因此，在定义各种函数的载荷曲线时，必须在函数设置窗口中启用平滑处理，以确保收敛性。瞬态求解器的任务是根据平滑过程的定义，求解载荷步骤之间的过渡问题。

分段 函数的 设置 窗口，定义了一个载荷曲线，突出显示了平滑的应用，以改进函数的数值收敛性。

此外，如果我们可以获得实验载荷循环测量数据，并希望将实验载荷曲线纳入电池模型，则可以使用 插值 函数将实验数据导入 COMSOL Multiphysics^®。例如， 瞬态集总电池模型的参数估计教学案例就使用了这种函数，将插电式混合动力汽车电池的实验动态载荷数据作为 集总电池 接口的外加载荷。

通过 插值 函数将实验动态循环数据导入 COMSOL Multiphysics^®，以确定外加载荷。

预定义充放电循环功能

如果要定义恒流/恒压循环分布，可以使用预定义的 充放电循环 功能，该功能可在电池模块中的所有电池和通用电化学接口中使用。使用此功能，我们能够模拟连续的恒流和恒压充放电循环，并可以选择在循环之间加入静置时间。如下图所示，用户可以自定义模式的顺序，指定静置时间，并分别设置恒流和恒压模式下的电压和电流阈值。在模拟时间允许的情况下，这组预定义的分布会一直重复。

充电-放电循环 节点的 设置 窗口包含两个独立的充电和放电模式，允许用户在窗口中选择包含或者不包含某些步骤，并输入相应的值。该节点将根据 启动模式 设置，以 充电 或 放电 模式开始循环。

该节点还包括一个循环计数变量，可在 结果 部分访问或用于在瞬态求解器中设置停止条件。单颗粒锂离子电池模型和锂离子电池的容量衰减教学案例中就使用了这个功能指定恒流和恒压分布。

内置节点 充放电循环 有一定的局限性：它主要依靠电压和电流阈值在模式间切换，这可能不能完全符合你的要求。对于更复杂的载荷循环，应该考虑使用 事件 接口设置循环行为。

事件接口

我们在前文的 函数 部分提到，在使用不同函数定义载荷曲线时应用平滑处理，可以解决求解器在载荷突然转换时的数值不收敛问题。在使用 事件 接口定义载荷曲线时，这种数值处理方法已被集成在内，因此可以增强用户模型的收敛性。事件 接口使电池仿真人员能够创建包含多个步骤和各种模式切换的不同载荷。这是通过确保载荷表达式包含一些通过 事件 接口定义的开关来实现的，从而允许一个载荷表达式采用不同的值。载荷表达式基于多个离散状态变量建立，通过改变这些变量的值，来定义所需的载荷曲线。

在深入讨论如何使用 事件 接口来定义所需的载荷曲线之前，有必要更深入地了解它的主要功能。您可以在 COMSOL Multiphysics^® 的 数学>常微分和微分代数方程 接口分支下找到 事件 接口。它主要用于创建求解器事件。这些事件可分为两类：显式和隐式。显式事件是预先确定在特定时间内发生的，例如在指定时刻按计划关闭载荷。隐式事件则在满足特定条件时发生，例如当电池电位达到预定的截止阈值时，需要修改外加电流或使电池处于静置状态。当触发事件后，瞬态求解器会停止，并更改一个或多个离散状态变量的值，然后重新启动。值得注意的是，充放电循环 功能是基于事件运行的，并已经“在幕后”预先定义了隐式事件。

要了解有关 事件 接口及其实践操作的更多信息，请浏览博客:使用事件接口模拟温控器。

现在，我们已经了解了 事件 接口的工作原理、关键组件，以及它如何让用户根据特定条件或在特定点上修改模型，接下来，我们就可以探讨它在载荷曲线定义中的应用。载荷曲线中的不同运行模式或步骤可以用一组 离散状态 来表示。当这些状态接收到不同的值，会像一组开关一样，随之改变载荷表达式的定义，如下图所示。决定使用显式还是隐式事件取决于当前载荷定义的具体情况。如果知道影响分布模式的变量变化的时间，就可以使用显式事件。在时间未知的情况下，可以通过一组 指示器状态 来详细说明这些变量发生变化的条件和标准，例如电池性能因素的特定阈值。指示器状态 会建立求解器用来触发隐式事件的状态变量。

在析锂变形模型中，使用 事件 接口创建包括正向和反向电流占空比的 事件序列。

在 变量 部分被定义为 “i_app”，并传递给 锂离子电池 接口中的 电极电流 条件的外加电极电流密度，是根据正向和反向状态计算出的。循环执行此序列，详请参阅事件序列 下面的 设置 窗口。

请注意，所有 隐式事件 和 显式事件 节点都会在指定时间或满足条件时触发。它们在接口中的定义顺序可能与分布中的预期变化顺序不一致。右键单击 事件 接口后，还可以使用另一个名为 事件序列 的选项，更直接地加入连续步骤。使用 事件序列 可以指定一系列事件，这些事件将按照列出的顺序激活。添加 事件序列 后，您可以包含多个序列成员，每个成员都根据条件表达式或特定持续时间运行。此外，使用 事件序列 后，可以在 事件序列 设置窗口中选择 循环 复选框。这样，只要仿真时间允许，事件就可以重复发生，从而灵活地定义重复的循环。

如果希望事件序列在研究过程中反复循环，请选择 循环复选框，如图所示。

通过在事件触发点为求解器设置 停止条件，隐式事件也可以终止仿真。这种方法通常比通过 停止表达式 定义的停止条件更加精确。如下图所示，在具有热力学电压滞后的硅-石墨混合电极模型中，定义的所有隐式事件都会自动列在表中，当任何标记为活动的事件被触发后，仿真就会停止。

当电极电位超过与 0% 电极充电状态 (SOC) 对应的定义电极电位时，隐式事件 2 被触发，并发出模拟结束的信号。

COMSOL Multiphysics^® 中有很多电池模型都采用了这种方法，例如：

• 析锂变形
• 锂电池设计器
• 锂离子电池内阻
• 锂离子电池的倍率性能
• 使用并联电阻进行电池过放电保护

结束语

在这篇博客中，我们探讨了在 COMSOL Multiphysics^® 中可以定义载荷循环的各种方法。我们通过几个案例模型演示了这些方法。这些宝贵的资源，可以帮助您了解如何在电池仿真中应用这些方法，以及深入学习在仿真项目中准确表示载荷曲线的最佳实践和技术。

小到玩具、无人机、手机和笔记本电脑，大到医疗设备和电动汽车，锂离子 (Li-ion) 电池被用于为各种各样的设备供电。为了有效地为这类设备供电，需要控制工作时的锂离子电池内部的温度分布，因为偏离最佳运行温度可能会导致其性能下降或失效。多物理场仿真是分析锂离子电池温度分布的一种方法。

在这篇博文中，我们将探讨如何对锂离子电池组中的热分布进行建模，并讨论基于该模型的仿真 App。

模拟电池中的热分布

电池的热建模通常使用两种方法完成：

1. 高保真建模
2. 集总建模

高保真建模可以详细了解电池的性能和行为。高保真建模可以深入了解电池，例如：电池单元内的电流和电势分布、电池内锂离子的浓度和传输、由于电池退化导致的容量衰减以及失效机制。虽然详细的模型可以深入了解单个电池单元，但计算成本太高，无法用于预测大型电池组的性能。此外，对于可能从电池制造商处购买电池的汽车制造商来说，很难测量或获取构建高保真模型所需的电池单元级模型输入参数。

对于完整的电池组建模，集总模型可以提供可接受的精度、较低的计算成本和较少的输入参数。集总模型需要输入参数，例如：

• 电池容量
• 初始荷电状态 (SOC)
• 开路电压 (OCV) 与 电池荷电状态
• 表征电压或容量损失的参数

对于电池组的设计者和制造商来说，这些参数很容易获得。我们在之前的博文中已经讨论过了如何使用参数估计来获得这些参数。

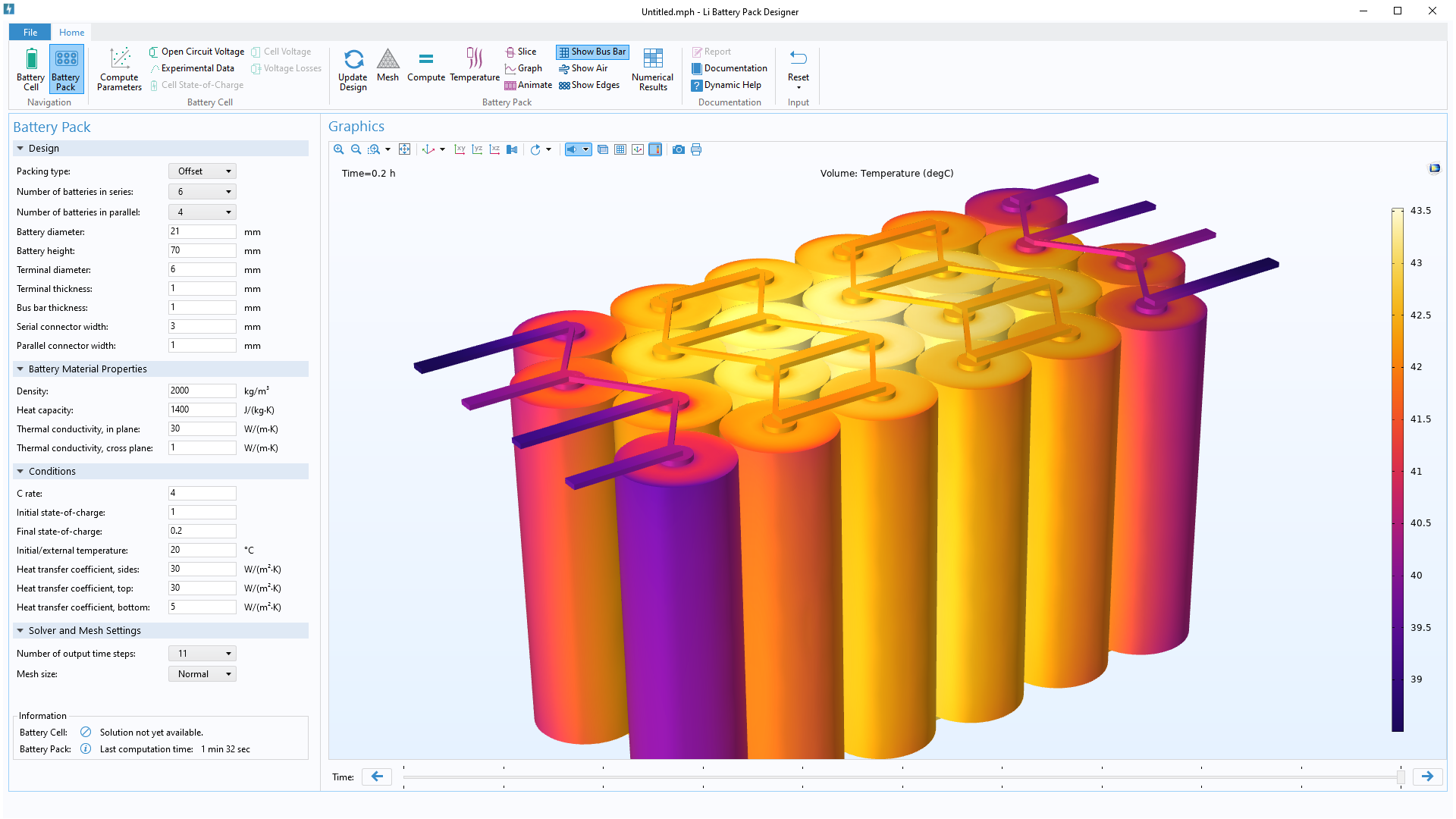
锂电池组设计器仿真 App 中呈现的由 200 个电池组成的电池模块的图示，文末我们将对其进一步讨论。

在下一节中，我们将分享一个使用集总建模方法构建的电池组热模型示例。电池组的几何形状设置为 3D，集总电池 接口用于定义单个电池的热特性。

请注意：如果你想一步一步地构建这个模型，可以随时点击此处链接下载：“圆柱电池组的热分布”。

COMSOL Multiphysics^® 中的集总建模方法

让我们看看如何建立电池组模型，并进行 4C 放电电流下温度分布的仿真。

我们要建模的电池组（或模块）由 6 对圆柱形电池组成，它们连接在一起形成 6 节串联、2 节并联 (6s2p) 配置，这种电池在玩具和医疗设备等便携式设备中很常见。请注意，相同的程序可用于对数百个电池进行建模，例如在汽车的电池模块中，详见上面的电池模组图。

使用两个对称平面可以确保只需要为三个单独的电池单元计算温度分布。我们添加了三个 集总电池 接口实例用于定义各自的热源，然后将它们耦合到一个传热 接口。

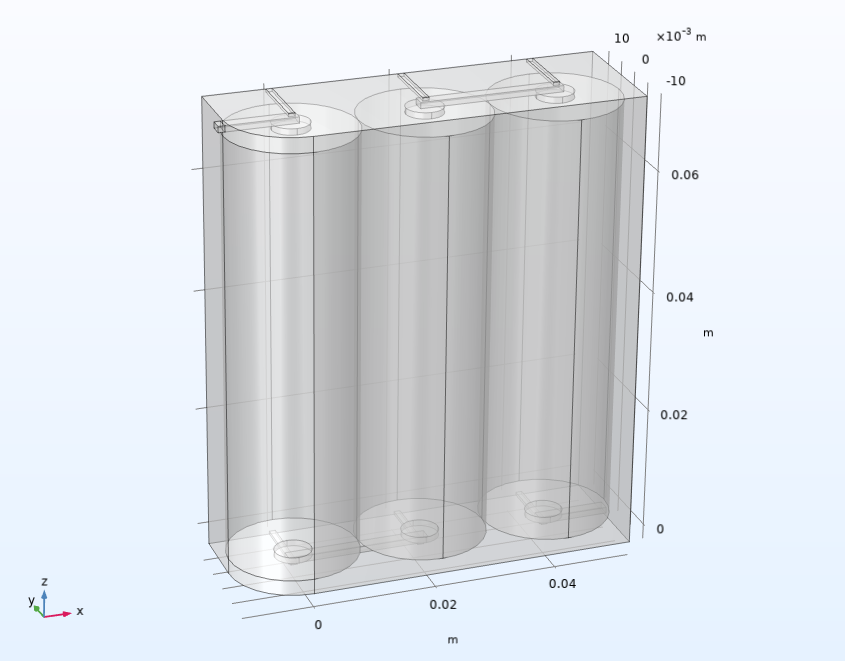
模型的几何结构。

电池组中电池的位置会影响其工作温度。在该模型中，三个 21700 圆柱电芯（直径 21 mm，高 70 mm）彼此相邻放置。根据 6s2p 配置，小的铝连接条位于气缸的顶部和底部。假设整个电池组用塑料包裹，形成一个充满空气的区域。假设每个电池的标称容量为 4 Ah，标称电压为 3.7 V，则该电池组的总标称容量约为 178 Wh。

用于对单个电池圆柱体进行建模的每个集总电池接口都具有与温度相关的欧姆、交换电流和扩散时间常数参数。温度曲线使用传热接口建模，其中源自电池模型的热源使用电化学加热多物理场节点添加；因此，每个单元都有一个单独的集总模型。

在这个模型中，我们选择忽略包围电池的空气域中的对流，假设处于静止状态。电池组的外边界采用对流冷却条件进行冷却。对于面向电池组其他部分的内部平面对称边界，使用对称（无通量）条件。

每个电池单元的热导率是各向异性的，通过圆柱坐标系定义每个电池圆柱体，遵循电池内部的果冻卷结构，该结构由电池内部的金属箔、电极和隔膜组成。与角度和z方向相比，果冻卷在径向上的导热率较低，这是果冻卷中螺旋缠绕的金属箔的结果。

电池组在 4C 放电倍率下持续 12 分钟，从 100% 放电到 20% SOC 。温度和电池电位的探针被添加到不同的电池中，以便在求解时直观地表示结果。

12 分钟后电池组的表面温度。

可以观察到，电池组最里面的温度比最外面的温度高出大约 2ºC，在更大的电池模组中，温度会升高到几十度。

如下左图中所示，最外层电池（电池 1）的放电电压略低，这是由于欧姆损耗和交换电流略低，在较低的温度下，扩散时间常数略高。对应的温度如下右图所示。

放电期间的单个电池电压(左)和一段时间内的平均电池温度(右)。

对含有 200 个电池单元的电池组建模

如前所述，上述电池组型号为 6s2p 配置；但是，下一节讨论的锂电池组设计器仿真App可用于对具有数百个电池的电池组进行建模。使用该仿真 App，在给定的工作电流下解决问题也只需要不到一分钟的时间！

由 200 个电池单元组成的电池组模型，由仿真 App 构建。

使用仿真 App 优化电池设计过程

非仿真专家也可以使用 COMSOL^® 软件强大的计算功能。COMSOL Multiphysics 中的 App 开发器 允许仿真专家创建用户界面友好的仿真 App，仿真 App 省去了与构建模型相关的细节，只关注用户希望控制的参数。

一个用户友好的仿真 App 示例是锂电池组设计器 App，你可在 COMSOL App 库中找到。用户可以首先使用实验数据估算出电芯的欧姆过电位、扩散时间常数、无量纲交换电流等参数。然后，可以选择电池组设计参数(电池组类型、电池数量、配置和几何形状)、电池材料属性和运行条件。最后，使用所选电池组设计中的参数化电池单元模型，可以整体模拟电池组的动态电压和热行为。

锂电池组设计器仿真 App。

下一步

下载模型文件和仿真 App ,尝试对锂离子电池的热性能进行建模：

• 教程模型：圆柱电池组的热分布
• 演示App：锂电池组设计器

拓展阅读

想了解更多关于锂离子电池建模的信息吗？您可以查看下列相关资源：

• 创新的电池设计仿真
• 分析锂离子电池组的液体冷却
• 混合动力和电动汽车有牵引力吗？
• 为什么汽车蓄电池在寒冷天气中表现欠佳？

最近，电动汽车和电池的领先制造商特斯拉公司发布了一种新型圆柱形锂离子电池的“无极耳”设计概念，这在电池专家中引起了不小的轰动（参考文献1）。特斯拉声称，这项创新设计使现有电化学体系下的汽车续航里程和功率显著提升。对于年度增速仅有百分之几的电池界来说，这是个难以置信的好消息。然而，在深入研究基本的电池物理特性后，我们很快就会发现为什么这种新的电池设计概念可以助力未来的电动汽车行驶更多的里程。在这篇博文中，我们将探讨这种新型极耳设计。

使用平面结构模拟电池

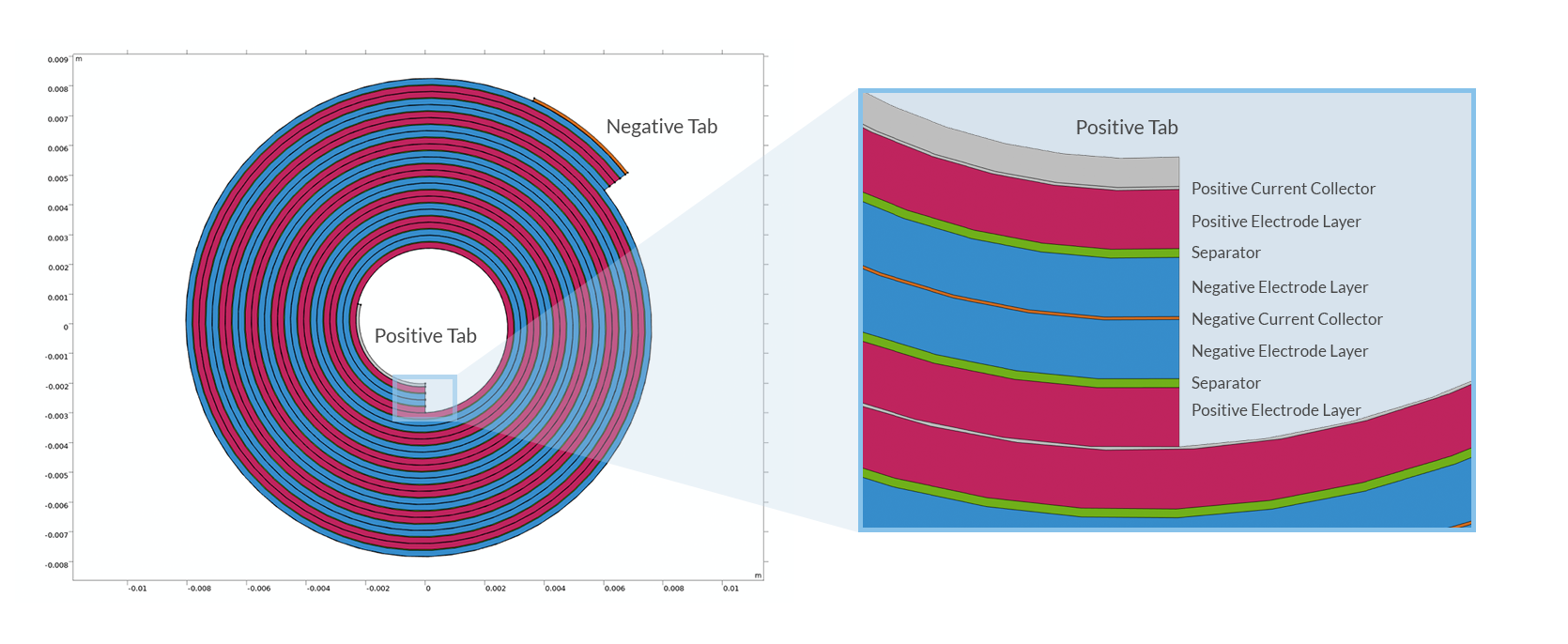
我们先从锂电池的构成说起：锂电池由不同的夹层构成，包括集流体金属箔、多孔电极和隔膜，它们被放在一个充满电解质的外壳中。夹层的配置取决于外壳的类型（纽扣电池、方形电池、软包电池和圆柱形电池，等等）。圆柱形锂离子电池的制造方法是先将不同的电池层卷绕成圆柱形卷筒，然后将其放进一个金属罐中，由此形生的螺旋结构通常被称为“果冻卷”，因为它与中欧的一种糕点非常相似。

用于圆柱形电池的螺旋缠绕果冻卷的横截面。

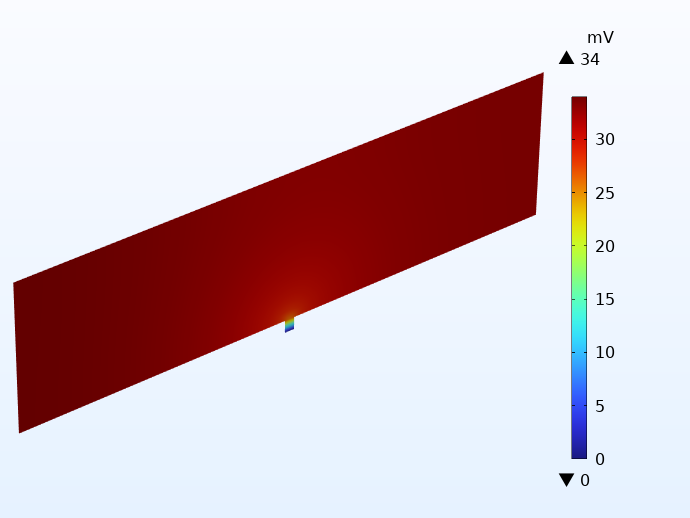
集电隔膜通常由铜（负极）和铝（正极）制成，二者的厚度都在几十微米左右，或者更小。选择不同金属的原因是它们在不同电位下的电化学稳定性。为了将进出果冻卷的电流传导到外部电池罐，在集电器上焊接了额外的金属条，也就是极耳。低功率电池的最简单的极耳设计，就是在果冻卷的每一侧放置一个极耳。

作为研究极耳效应的第一种方法，我们可以创建一个伪稳态模型，该模型解释了电子导体和电解质中的欧姆电压损失，以及由于电极中的电荷转移反应引起的激活过电位。在这种情况下所产生的施加在电池上的电流内部分布被化学家称为二次电流分布 。由于该模型没有考虑电极中锂原子或电解液中锂离子的积累或耗尽，因此可以将其看作在特定荷电状态下电池的瞬间冻结。实际上，当电池充电或放电时，局部浓度会随着时间而变化。然而，二次电流分布模型可以准确地预测给定充电状态下给定时刻果冻卷中的电压损失。

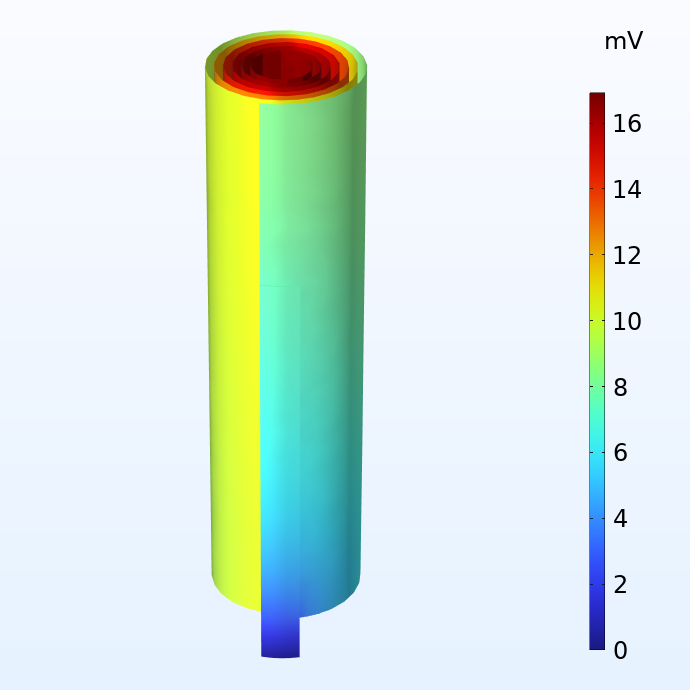
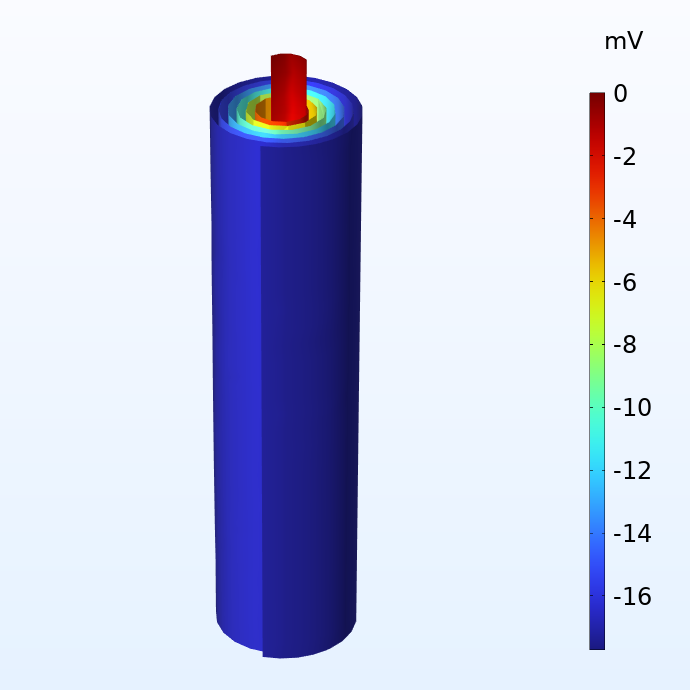
负极（左）和正极（右）集电器薄膜中相对于相应电流端子的电位。

上图显示了一个果冻电池在受到 1 C 放电时负极和正极集流体上的电位分布。1 C 是在一小时内对电池进行充电或放电所需的等效电流。这个果冻卷的尺寸与 18650 电池罐相同，高 65 毫米，直径 18 毫米。我们注意到，尽管集流体的潜在损失非常小，却不容忽视。对于特斯拉计划生产的更大的电池，如 4680 电池（高 80 毫米，直径 46 毫米），如果使用传统的极耳设计，电压损失会非常大。

由于我们的模型是基于物理场建立的，因此可以根据欧姆损耗（焦耳热）和激活过电位轻松推导出局部热源。将热源变量引用到传热模型，我们得到以下结果。

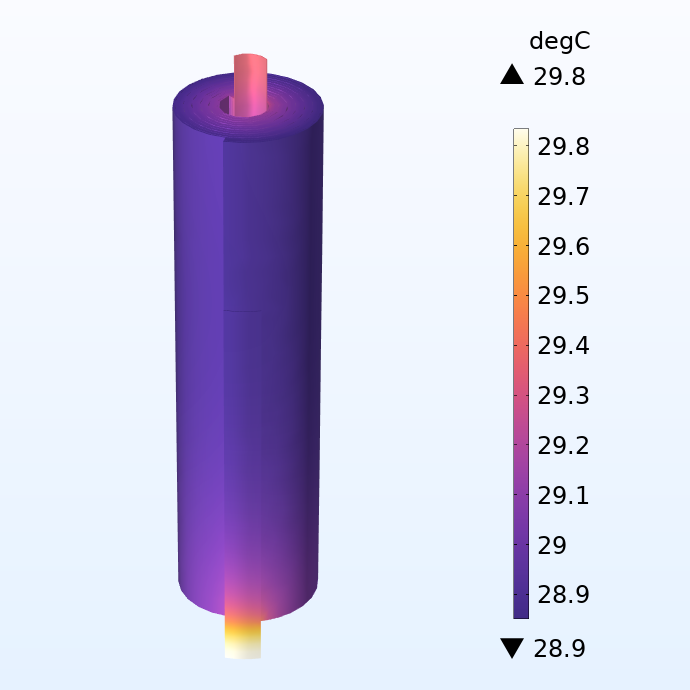
果冻卷中的温度分布。

在模拟中，我们在果冻卷的外部区域施加了对流冷却条件，规定了与表面温度和外部温度（25°C）的差异成比例的冷却热通量。忽略了通过极耳末端的电气端子传导的热量。

如果查看温度分布，我们可以看到极耳中的温度急剧上升。这表明，对于这个极小的电池，即使在中等电流下，极耳中的焦耳热也会导致明显的局部加热。局部温差也可以传播到相邻的电极层，导致电池的某些部分老化得更快，从而缩短整个电池的寿命。

在进行建模和模拟时，建立真正的果冻卷几何形状有点麻烦。在一个螺旋几何图形中绘制对象很困难，例如在果冻卷的内部添加多个极耳。此外，很难将螺旋层内部的结果可视化，例如绘制通过卷中不同位置的极耳的电流密度。

模拟一个扁平的果冻卷

我们可以在一个扁平的（展开的）果冻卷几何图形上定义相同的模型。这样我们能够轻松地引入极耳并更方便地查看模型和仿真结果。建立扁平化模型后，我们可以虚拟地滚动电池。下图显示的是一个扁平的果冻卷几何图形，不同的层和极耳被绘制为矩形块。

螺旋果冻卷几何图形的扁平化表示。

实际上，当由夹层堆叠创建果冻卷时，前（绿色）边界最终将与矩形块堆叠层的后侧接触，见上图。为了在数学上将这些在几何上分离的边界连接在一起，我们使用了特殊的耦合边界条件，即 COMSOL Multiphysics^® 软件中的非局部耦合建立扁平果冻卷模型。这就是我们上面所说的虚拟滚动电池的意思。

扁平几何形状另一个的优点是需要较少的网格单元，因为不需要解析卷的局部曲率。令人欣慰的是，扁平几何形状的温度曲线准确地再现了果冻卷的模拟结果，见上文。这表明我们可以进行这种扁平化转换，而且对结果的影响很小。

扁平化果冻卷中的温度 (°C)。

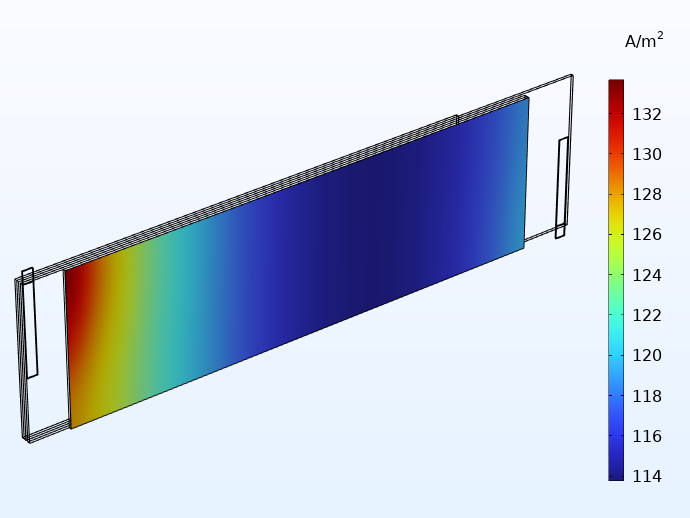
现在我们可以在扁平的几何形状中轻松可视化交错隔膜的电流密度，如下图所示。

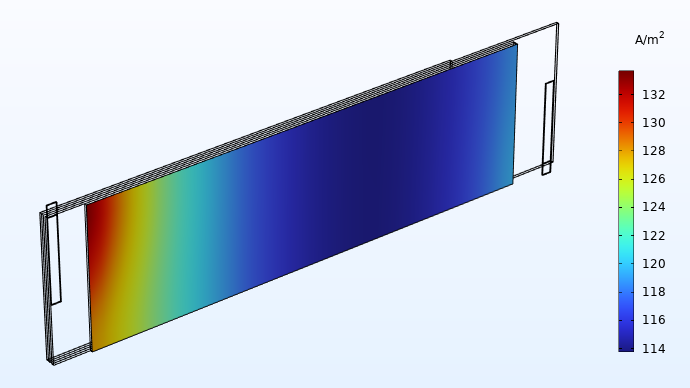
一个隔膜在平面方向的电流分布(A/m² )。

像这样的电流分布图可以为电池设计人员提供非常宝贵的意见。在这个示例中，上图显示了在靠近极耳的区域，电流密度明显更高。这意味着电池在靠近极耳的区域会受到更多的电化学磨损，从而加速老化。如果让电池运行更长的时间，上面的电流分布图最终会变得更均匀。对于在固定荷电状态下循环 时间较短的电池（例如，负载均衡电池系统），上述电流分布的评估将相当准确。

用 COMSOL Multiphysics 研究集成极耳设计

现在让我们使用上述建模方法来研究所谓的无极耳设计。

无极耳的概念意味着移除额外的金属条极耳，使用集流体金属箔将电流传导到外部。这是通过将箔片延伸到电极区域以外来实现的。由于箔片非常薄，因此需要大量延伸的金属箔条以防止出现大的欧姆电阻。术语“无极耳”有点误导，因为极耳实际上是被集成到箔片中了，而不是完全移除。因此，我们在本博文的其余部分使用术语 集成极耳 来表示 无极耳。

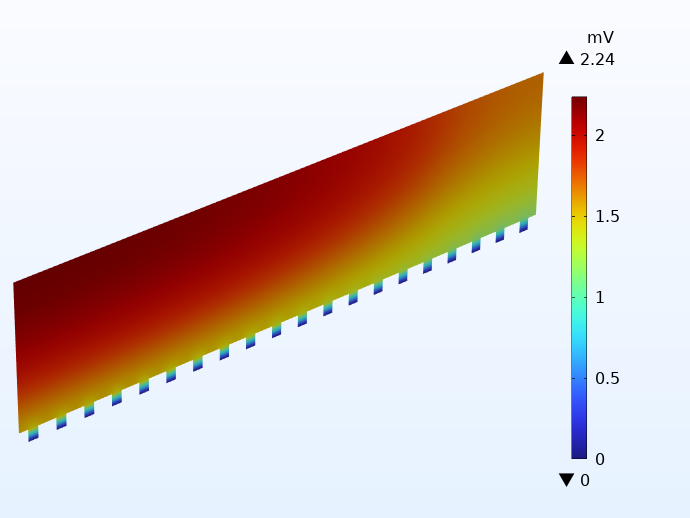
为了说明在实践中是如何工作的，下图显示了两个使用了集成极耳的电池负极集流体箔片中的电势分布。除了极耳配置之外，这两个电池与上面的示例完全相同。左图示例仅使用了 1 个极耳极耳，右侧示例在每侧使用了 20个极耳。注意两个电位图例的不同，它们的尺度相差超过了 30 mV！

使用集成极耳比较两个电池的负极集流体中的电势：1 个极耳（左）和 20 个极耳（右）。

这表明使用一个集成极耳会产生非常大的潜在损失，从而导致大量的局部热源。对于具有许多极耳的电池，其潜在损失低于使用传统极耳的电池。

带有一个集成极耳的示例应该被视为一个极端。但我们还希望通过使用不超过需求的极耳来节省金属和电池的重量。为了研究极耳数量的影响，我们可以进行参数化扫描研究并绘制极耳数量与电池的总极化和最高温度的关系。

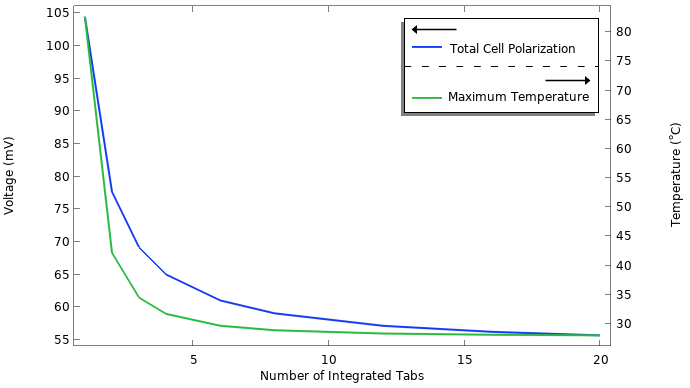
电池总极化和最高温度与集成极耳的数量的关系。

如图所示，当极耳数量增加时，总电池极化曲线和温度曲线开始快速地接近渐近线。我们可以看到，添加 20 多个集成极耳金属箔条不会将电池极化降低到 55mV 以下。剩余的电池极化来源于不受极耳数量影响的其他过程，例如电解质的电阻和电荷转移反应。我们还看到，仅使用一个或两个极耳并不可取，因为温度会上升到非常高的水平。高温会加速老化，也是一个直接的安全隐患。

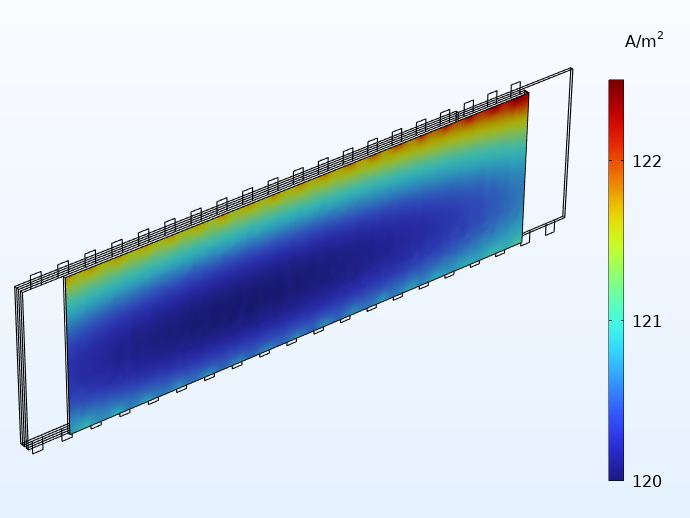
下图比较了使用集成极耳和传统极耳的电流分布。我们看到，集成极耳的电流分布更加均匀。此外，使用集成极耳时仍然存在小分布效应，主要沿着果冻卷的高度方向。

使用 20 个集成极耳（左）和传统极耳（右）时，流经卷层方向的电流分布。

当涉及到热传递时，集成极耳可改善果冻卷的内部冷却。这是因为通过优良的热导体金属，极耳与外部冷却表面进行了热接触。每个极耳都与外部进行了热和电接触。

下图显示了带有集成极耳的果冻卷电池的温度分布。从这张图中我们可以看出，与传统的极耳相比，这个果冻卷电池的温度场分布更加均匀。

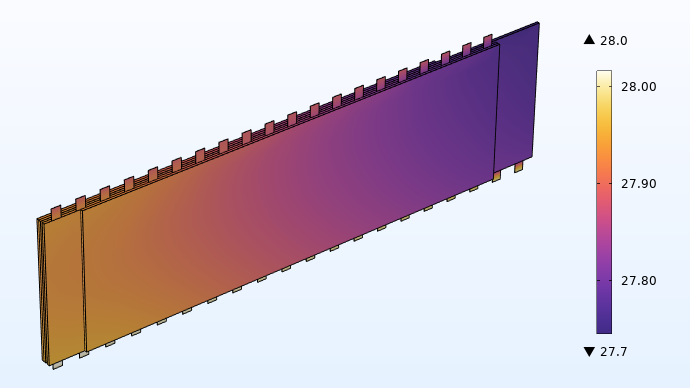
使用 20 个集成极耳的温度 (°C) 分布。

结束语

综上所述，集成极耳显著改善了电流的传导和电池外的热量传导。这使得制造具有更大半径的圆柱形电池成为可能，同时可以提供更高的电池组整体能量和功率密度。更大的电池半径使内部电池材料量与电池的外壳（罐）之间的比例更大。这也解释了特斯拉为什么会提出“无极耳”的设计概念。

“无极耳”设计被证明是传统锂离子电池极耳的创新替代方案。然而，它也带来了新的工程挑战，这个可以在 COMSOL Multiphysics 软件中进行评估。

下一步

• 通过下载这些教程模型，了解如何使用果冻卷方法进行仿真：
  • 圆柱卷绕式电池
  • 使用扁平几何模拟圆柱卷绕式电池
• 查看相关的博客文章，了解更多内容：
  • 分析锂离子电池组的液体冷却
  • 了解电化学模型：柠檬电池
  • 使用 COMSOL^® 平衡锂离子电池的电极
• 查看Tesla 对“无极耳”方法的演示

参考文献

1. A. J. Hawkins, “Tesla announces ‘tabless’ battery cells that will improve range of its electric cars”, The Verge, 22 Sep. 2020; https://www.theverge.com/2020/9/22/21449238/tesla-electric-car-battery-tabless-cells-day-elon-musk

在本篇博客文章中，我们将讨论如何从头开始建立电化学和电池模型的一般过程，并以柠檬电池为示例来演示建模过程。

柠檬电池简介

柠檬电池是学校化学课中的一个经典实验。使用一个柠檬、一块铜（例如，一枚硬币或一些铜线）和一块锌（例如，镀锌的钉子），可以制造一个能为小型电子设备供几分钟电的电池。但是，众所周知，这种电池的适用性受到限制，因为它的功率只有几毫瓦（mW）左右。

带有两个电极的柠檬（左：铜；右：锌）。

建模目标

在建模之前，建模人员应该提出的第一个问题是：我们这个项目的建模目标是什么？这看似微不足道，但如果在这个问题上花点时间，通常可以节省很多时间。

对于本文的示例，我们将解决以下问题：柠檬电池随时间的输出功率受到什么限制，如何加以改进？

换句话说，就是我们希望把这个模型用作一个设计工具，以将电池功率提高到 1 mW 以上。而其他常见的建模目标可能是减少体积、重量和（或）成本。

功率输出与电极终端上的电压和电流直接相关。这意味着我们的模型需要包括电池中电压源和引起电压损耗的主要来源，而估算电流意味着也需要以某种方式考虑电荷（离子和电子）的传输。此外，时间 也是必不可少的，这意味着我们需要包括瞬态变化。

我们可以采取什么措施来提高功率？有时一开始很难知道，但考虑到材料（柠檬、铜和锌）本身就是设计的约束，因此我们可以做出一个可能的假设：提高柠檬电池性能的唯一方法是改变电极的几何结构。

综上可知，我们需要定义一个与时间和空间有关的 模型。

化学物质和反应

现在，我们来讨论要在模型中添加哪些化学物质和反应。

在查看柠檬的营养信息后，我们发现电解液由柠檬酸（300 mM = 0.3 mol/L）和抗坏血酸（3 mM）组成，它们都是弱酸，缓冲至 pH 值在 2 左右（对应质子浓度为 10 mM）。电解液中还有其他离子 的混合，最主要的阳离子是钾（35 mM）和钙（7 mM）。在插入电极之前，柠檬中已经存在痕量的锌（9μM）和铜（6μM）离子。除此之外，因为存在大量阴离子（例如氯离子）与阳离子匹配，所以本体电解液经常是呈现电中性的。

鉴于两个电极分别由金属铜和锌组成，并且它们可能会溶解，因此以下电极反应似乎值得进一步分析：

 
接下来，我们将根据柠檬的营养信息使用能斯特方程 计算指定浓度下的平衡电位，E_eq。电极反应式中我们用了双向箭头，表明反应是完全可逆的，并且可以在任何方向进行。

由于电解液是含水的，而水在整个柠檬中均匀地发生自电离作用，因此存在质子 和氢氧根 离子：

 
但是，由于 pH 值是酸性的，我们认为氢氧根离子浓度可以忽略不计。

在水性体系中，可能会形成金属氢氧化物。但是，查阅锌和铜的 Pourbaix 图 可以发现，由于 pH 值较低，不太可能在柠檬中形成金属氢氧化物。

电解液是水性的，这意味着由于电极电势的存在，氧 和氢 都可能在电极上形成或消耗：

 
这两个反应都可能在两个电极上发生，尽管我们通常假设铜电极上的动力学更快。

在柠檬的营养信息清单中，我们发现钾和钙的标准溶出电位远低于锌和铜的溶出电位，这意味着它们不会大量沉积在任何电极上。同样，氯气析出的标准电位要高于氧气，因此在本模型中也可以忽略不计。

多种不同金属离子的存在与混合电极电位的结合，导致可能产生相当复杂的金属沉积副反应系统，特别是在锌电极上。例如，柠檬中的痕量铜离子或任何其他贵金属离子可能会沉积在锌电极上。这可能会改变该电极的电催化性能，例如，沉积的铜可能会显著增加析氢的活性。在这一点上，我们选择忽略这些影响，并假设金属铜和锌的沉积溶解仅在其各自的电极上发生。

弱酸（柠檬酸和抗坏血酸）分子相对较大且复杂，通常会导致动力学变慢，我们简单地假设它们在电极上不发生反应。此外，我们还忽略了弱酸与金属阳离子络合物的形成。至于营养清单上的其他种类（糖、脂肪等），我们也予以忽略。

电解液传输

现在，我们来看看电解液中的传输过程。

首先，我们需要确定电解液中电荷传输和电位的模型，因为电解液电位和金属电位之间的电位差是电极反应的主要驱动力。

由上文可知，大量的离子（K⁺, Cl^–等）不参与电极反应，这允许我们进行支持电解质假设，即电解液的电导率不随着电极反应而显著变化。因此，我们可以假设电导率恒定（0.35 S/m），并使用欧姆定律的偏微分方程求解电解液电位。

参与电极反应的离子包括 Cu ²⁺，Zn ²⁺，H⁺，H₂ 和 O₂，因此需要在模型中以某种方式定义这些物质的浓度（化学活度）。

Zn(s) 和 Cu(s) 的化学活度为常数 1，无需进一步处理。我们还假设电极的形状不会由于金属的溶解而改变。

与纯水（55.5 M）相比离子浓度低，我们可以假设电解液被稀释了。这意味着我们可以假设电解质仅与作为溶剂的水分子相互作用。

使用稀溶液假设，可以使用 Nernst–Planck（能斯特-普朗克）方程定义 Zn²⁺ 和 Cu²⁺ 的传输，这里我们只需要为每个离子设定一个扩散率/迁移率参数。

由于弱酸（柠檬酸和抗坏血酸）具有 pH 缓冲能力且不参与电极反应，因此我们假定 pH 值恒定（氢浓度）。

柠檬外表面周围的空气中的气体（氮气、氧气、二氧化碳等）可能溶解并扩散到电解液中。这里，我们将除氧气以外的所有气体视为惰性气体。假定氧气与柠檬外表面的周围空气处于平衡状态，它可以从表面扩散到电极，在电极处被还原。氧的扩散过程也可以用 Nernst–Planck 方程来描述（相当于不带电物质的菲克扩散定律）。在本系统所有的化学反应中，由于氧气还原反应具有最高的平衡电势，因此我们不必考虑氧气的析出。

对氢的传输过程进行建模有些困难。氢的还原/氧化反应平衡电位处于本反应系统的中间值，这意味着该反应可以沿任何方向进行（取决于局部电极电位）。如果在电极上形成氢气气泡，则会使建模复杂化，因为这会在系统中引入第二相（除了液相）。两相系统的建模通常很复杂，对于柠檬果肉，没有直接的方法来描述气泡传输。因此，我们假设所有氢均以气体形式（活度为1）形成，并且假定任何形成的气体在被氧化之前会立即被排出，以简化此过程。在方程式方面，就只能通过假设氢气反应为不可逆的还原反应（析氢）来实现。对于正（氧化/阳极）极过电位，将反应速率设置为 0。这样，模型无需求解氢浓度。

系统边界和几何选择

当包含锌和铜片时，由于这些金属相对于柠檬果肉具有很高的电导率，因此只要将金属的电位建模为边界条件就足够了。结合上文中的讨论可知，所建电池模型完全由电解液（柠檬的果肉）中发生的物理化学现象以及电极表面上的反应决定。因此，我们选择柠檬的外表面（不包括金属域）作为系统边界。

在构建模型几何时，考虑到对称性，我们将柠檬取一半建模以节省计算资源。

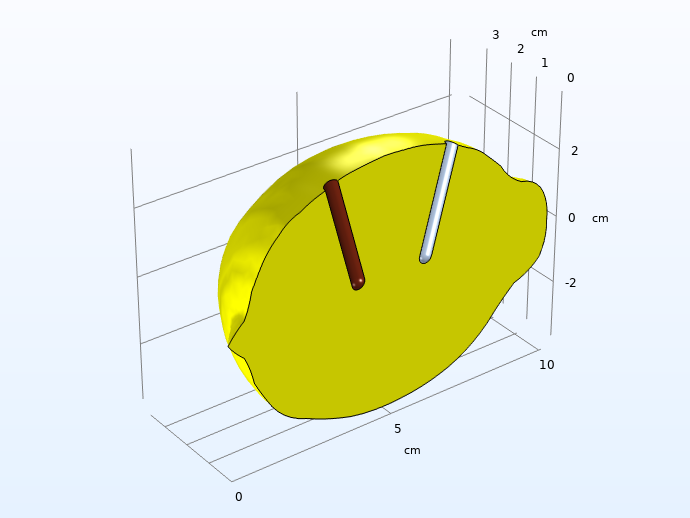
考虑电极的对称性和高电导率后的计算域。

注意：我们始终建议使用尽可能低的维度，因为这通常可以节省模型开发和计算时间。对于实际的柠檬，我们可以考虑围绕中心轴具有轴向对称性的二维几何。由于我们要完全自由地放置电极，因此必须在三维中构建模型。但是，即使在我们的示例中，仍建议以较小的维度开始建模项目，以测试不同的域方程和边界条件并确保它们收敛。例如，该模型适合首先在一维中建模，模拟在电解液中插入两个平面电极，但是在本博客文章中我们省略了此步骤。

在 COMSOL Multiphysics^® 中模拟柠檬电池

我们使用 COMSOL Multiphysics 中的 三次电流分布，支持电解质 接口对柠檬电池进行建模，下文显示了建模结果。我们使用恒定的电导率定义电荷传输，通过 Nernst–Planck 方程定义物质传输，基于软件内置的质量作用定律 Butler–Volmer 方程定义电极反应，以及基于 Nernst 方程计算平衡电位。

此处请注意：大多数参数值，尤其是电极动力学的参数值，仅出于示范目的，并非基于文献。

在模拟中，使用的负载循环包括：在初始条件（柠檬营养成分列表值）下搁置 1 min，然后在 0.5 mA 的负载下放电 1 min 分钟，再搁置 1 min。

解释电池运行期间的电压曲线

下图显示了仿真的电压和电流结果。

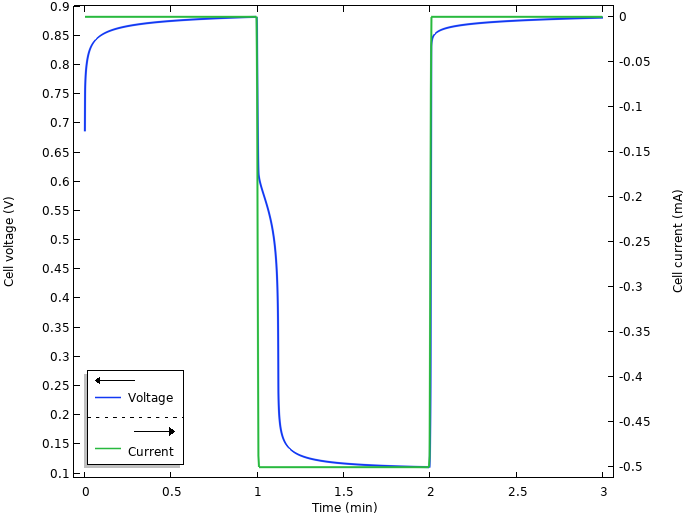
电压和电流。

最初，当将电极插入柠檬中时，似乎会发生某种弛豫，电池电压缓慢升高至 0.9 V。当在 t=1min 时接通电流时，电流会从开路电压下降到约 0.1V 的工作电压。我们还注意到，2min 后电流被切断会有某种弛豫。

将电池电压乘以电流，还可以绘制出电池的功率输出图。

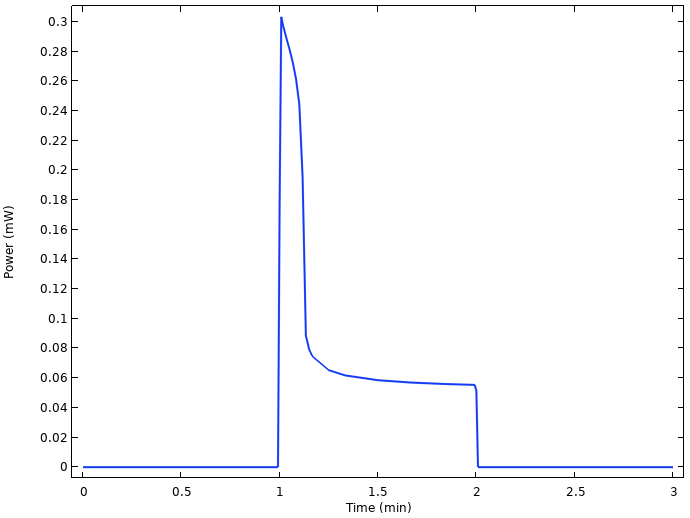
电池输出的功率。

由上图可知，负载接通后仅几秒钟，功率就从 0.3 mW 降低到 0.06 mW，这与电压大幅下降相有关。

当有电流通过时，电池电压下降大约 0.75V。如此巨大的下降（对于电化学家而言）意味着什么？下面，我们通过绘制两个电极端部的电极电位（相对于 SHE）与时间的关系来分析：

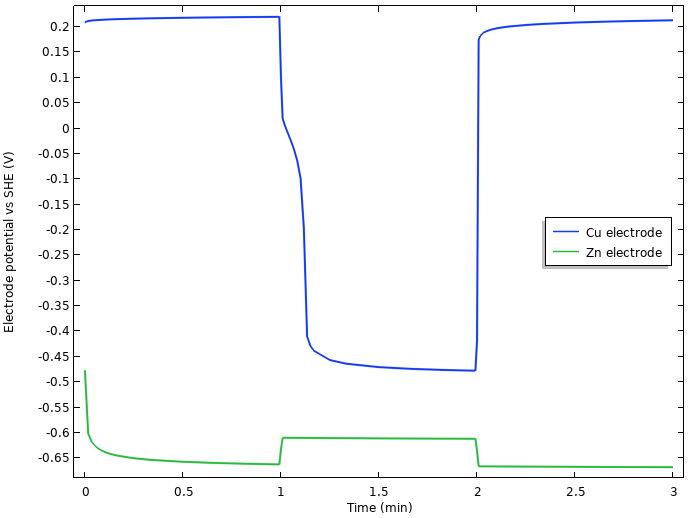
电极电位与 SHE 的关系。注：SHE-标准氢标参比电极

我们注意到，静止时电池电压的初始升高，似乎与负锌电极上发生的现象有关，但是当电流负载开启时，电池电压下降的 0.75 V 似乎大部分都来自于正铜电极。

下图中绘制的铜钉表面的平均氧气浓度与时间的关系揭示了这一现象。

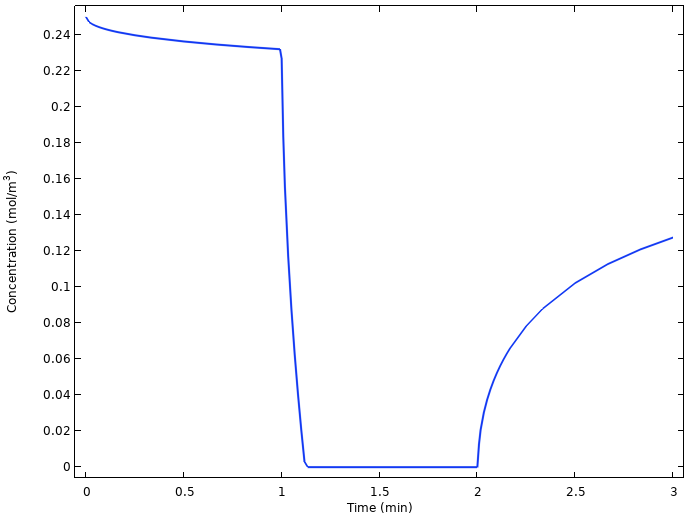
铜电极上的平均氧浓度。

当电流接通时，铜电极上的氧浓度迅速降至零，并在电流再次断开时开始弛豫并恢复到较高的值。原因是一旦打开负载，氧气从柠檬表面到铜电极的缓慢扩散不足以维持电池电流。也就是说，我们在高于氧气还原极限电流的条件下操作电池。

通过绘制整个铜钉表面不同电极反应的局部电流密度的积分，可以进一步解释该现象。

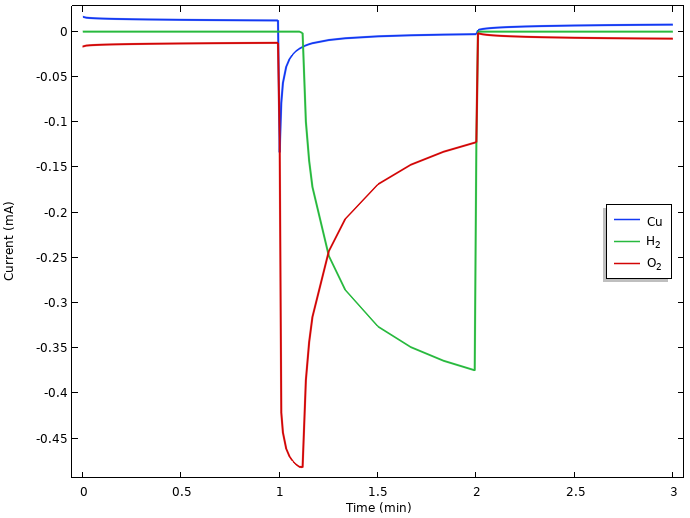
正极的局部电流密度积分。

仔细查看上图中初始搁置期间的电流，我们会发现：铜的溶解速度（小的正电流）与氧的还原速率（小的负电流）相同。这表明在搁置期间会发生持续的铜腐蚀。在最初的搁置期间不存在氢逸出。这是由于析氢的平衡电位低于此时的混合电极电位，其值位于铜溶解和氧还原的平衡电位之间。（但是，如果电极上已经存在氢气，则该氢气会被氧化。不过如前文所述，在任何时候我们都不会假定柠檬中存在氢气。）

接通电流后，我们会看到氧气还原电流出现初始激增，然后随着氧气耗尽而回落。由于我们操作电池的方式，所有电流总和被限制为总计 0.5mA 的电池负载，因此当电极中的氧气用尽时，电位会下降，直到达到低于析氢的电极电位，然后析氢反应才可以介入提供所需的还原电流。由于水的自电离作用和高的水浓度，在电极上有大量的氢离子供应，氢析出的极限电流比氧还原的极限电流高几个数量级。我们还注意到，当负载期间电极电位下降时，铜开始沉积。

因此，我们可以从由搁置状态下的铜溶解-氧还原控制的电极电位过渡到接通负载时析氢控制的电极。从搁置时约 0.2 V vs. SHE 的电极电位到接通时约 -0.45 V vs. SHE 的电极电位，这一较大的电位降可以通过氢气析出的平衡电势显著低于氧气还原的平衡电势来解释。动力学也影响着结果，但这里我们暂时不分析。

负极自放电和电池容量

下图显示了负极上各个电极反应的局部电流密度积分。

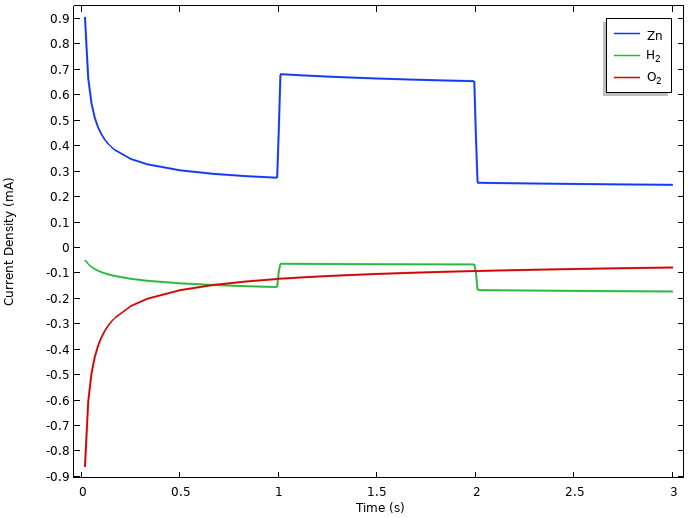
负极上的局部电流密度积分。

在负极上，氧气还原和氢气释放都会导致锌在搁置状态下溶解（最初的弛豫现象与所有这些反应之间的相互作用有关，但在此我们将不再进一步讨论）。

在负载期间，锌的溶出度增加，以匹配 0.5 mA 的电池电流，此外还要加上氧气还原和析氢电流

锌的连续溶解表明，我们放入柠檬中的金属锌的初始质量决定了电池的容量。因为在正极，水的自电离作用将为我们提供几乎无限量的氢离子来源来进行析氢反应。但是，电池能够放电的时长将取决于负载和自放电反应之间的相互作用。

评估电压损失

在负载期间，模型中存在三种主要的电压损耗源：

1. 电解液中的欧姆压降
2. 驱动锌在负极上溶解的活化过电位
3. 驱动正极上析氢反应（或氧还原）的活化过电位

首先，我们绘制了负载脉冲30秒后电解液中的欧姆电压降。

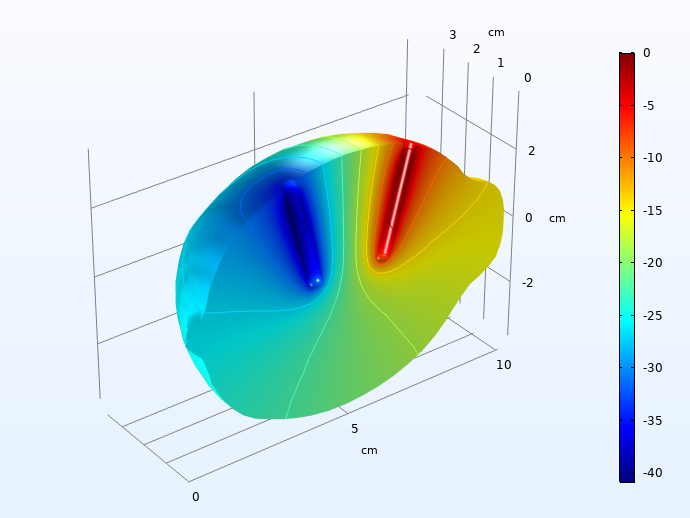
进入充电脉冲 30 秒后，电解液的欧姆电压降（mV）。

40 mV 的电压降很明显，但并不大。

接下来，我们绘制了锌在负极上溶解和氢气在正极上析出的局部过电位。

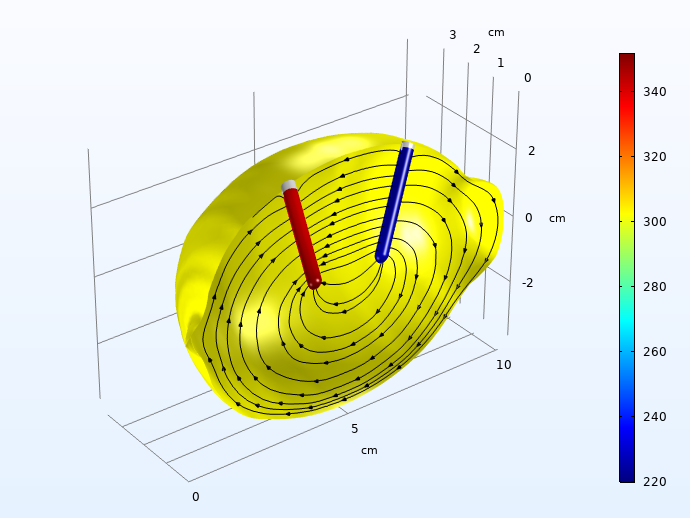
进入充电脉冲 30s 后，氢（左）和锌溶解（右）活化过电位（mV，绝对值）。流线描绘了沿对称平面的电解液电流。

两个电极上的活化过电位在负载脉冲中持续了 30s，总计约 0.5V。远高于电解液中电荷传输的欧姆损耗。

提高功率输出

现在，我们返回到最初的项目建模目标，查看是否可以提高电池的输出功率。

在不更改电极或电解液的情况下，很难实现改善锌电极上固有的电极动力学，以及对电池极化贡献最大的一组参数值。但是，我们可以通过增加可用的电极-电解液界面面积来改善催化活性。这样做的原因是，所有电流都必须通过每个电极上的电极-电解液界面，并且与电极反应相关的电压损耗越高，局部电流密度就越高。通过增加用于电极反应的可用面积，减小了每个电极面积的局部电流密度，进而也减小了相关的电压损耗。

由于柠檬中有大量的可用空间，因此，较大的电极几何区域（或只是更多的电极）应该是提高性能的可行方法。然而，这也将增加自放电，因为这也与活性电极面积直接相关。

如果可以减少电解液中的欧姆压降，电池性能也会稍微提升。实现此目的的一种方法是简单地将电极彼此靠近放置。但是，我们必须谨慎行事，因为这样可能会增加在锌电极上沉积铜的影响——而这可能会使锌电极的动力学降低。但是，我们尚未在模型中包括此类影响。

还有一种方法是，如果能通过某种方式利用铜电极上的氧还原而不是析氢反应放出 0.5 V 的电压（参见上图），则可以使电池性能提升。一种可能的方法是将铜电极放置在更靠近柠檬表面的位置，以缩短氧的扩散距离。

根据上面的建模结果，我们提出以下针对柠檬电池的功率优化设计。

功率优化后的柠檬电池设计。

在此设计中，我们用铜硬币替换了铜钉，还引入了多个电极（柠檬的每个楔形区域配一对电极，总共 12 对）。这里也许应该指出的是，新设计的布线工作将需要相当灵活的手指。

引入多个金属电极会增加电极的总表面积，应该可以以更高的总电流运行电池（原则上，我们现在并行运行了 12 个电池）。引入铜硬币而不是钉子，进一步增加了电极面积，但更重要的是，还增加了位于柠檬表面附近的铜电极表面数量，可以得到更高的氧气还原极限电流。

运行新设计模型的仿真，当总电流为 6 mA（每个楔形区域为 0.5 mA）时，电池电压如下图所示：

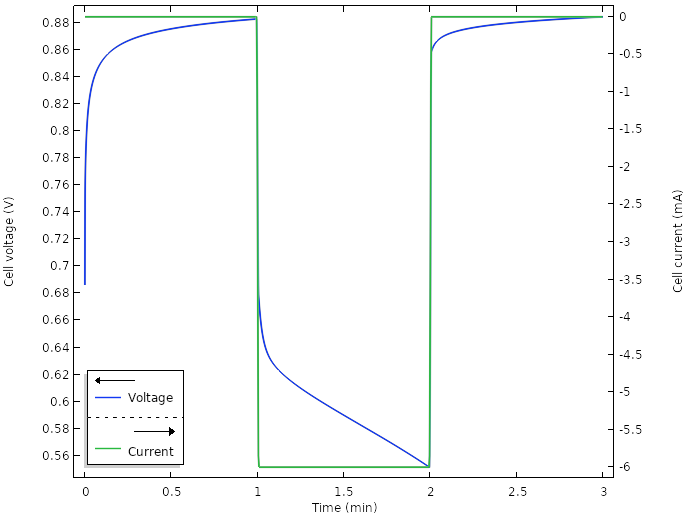
新设计电池的电压和电流。

相应的电池功率结果表明，现在我们能够在高于 1 mW 的功率水平上运行电池：

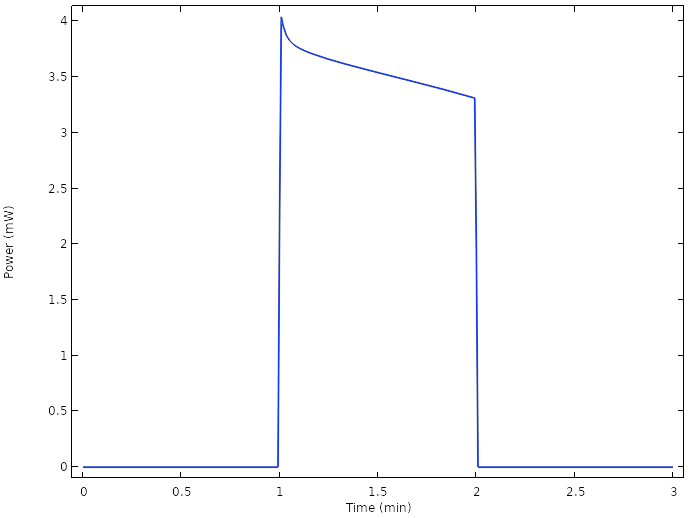
新设计电池的功率。

使功率提升的一个主要的贡献是使用了多个电极，但是绘制电极电位图表明，我们已经设法在输出电压超过 0.5 V 的情况下增加了正极电位。

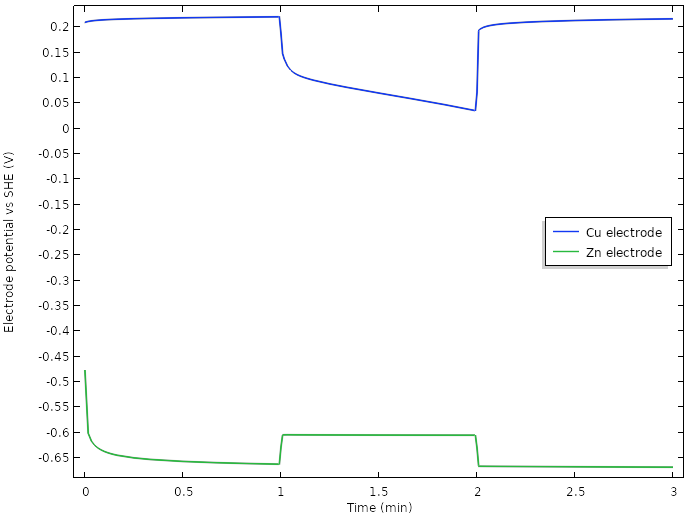
对于新设计电池，电极端部的电极电位与 SHE 的关系。

再次检查铜电极上的氧浓度，我们发现在任何时候都没有将电极上的氧完全耗尽。

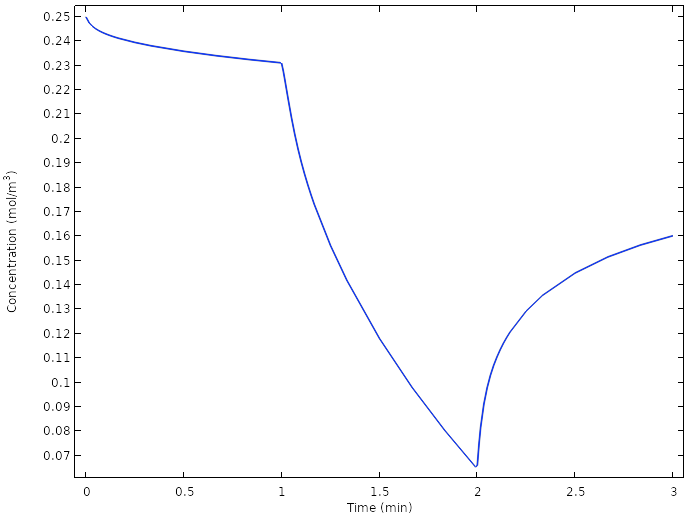
新设计电池铜电极上的平均氧浓度。

相应地，正电极反应电流的曲线表明，负载期间的主要电极反应是氧还原反应。

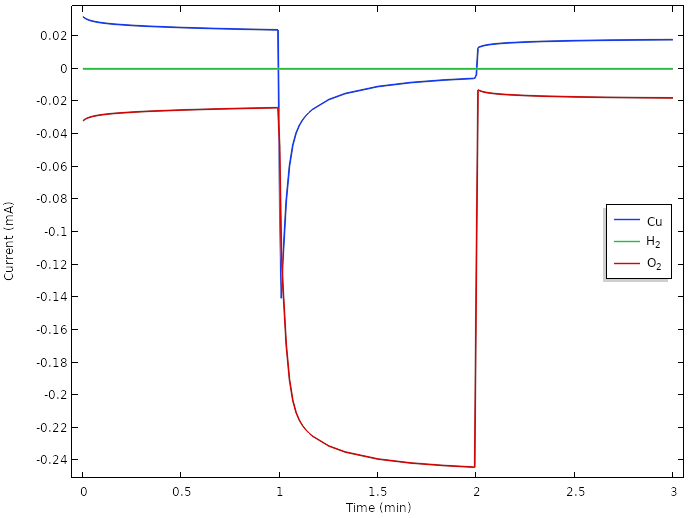
然而，氧浓度和电流都随着时间连续下降。进一步改进的方法是引入疏水性多孔气体扩散介质，以促进氧气在柠檬表面和铜电极之间的传输。由于气相扩散通常比液体扩散快约4~5个数量级，因此这将显著增加氧气的传输。如何执行此操作的详细信息非常适合使用模型来探索。也许，我们还必须将铜金属替换为对氧还原更有活性的物质，例如铂。但是，铂金硬币往往很难获得。

如今，人们已经发明了以这种方式设计的柠檬电池，它被称为锌空气电池，但其电解液是碱性的。

后续操作

对电化学建模的其他示例感兴趣吗？请单击下面的按钮，在 COMSOL “案例库”中探索更多电化学模型。

锂可用于各种场合，不过用在电池上可能是最引人注目的。锂离子电池可用于电动汽车，储能系统等。当锂离子电池用在这些领域时，工程师必须首先通过电化学分析确保其性能能够达到预期。当电池由第三方制造时，可能会带来一个问题：生产厂商不会向工程师透露有关锂电子电池的关键信息（例如内部结构等）。让我们来看看如何通过集总模型估算锂离子电池的参数。

锂离子电池的优势和设计挑战

锂是 元素周期表 的第三个元素，具有许多特别的特性。它与碳酸盐类药物结合使用时可以作为情绪稳定剂，这是一个 治疗暴躁症 的有效方法。对其进行加热时，它会产生红色，这有助于为烟花上色。锂是元素周期表中最轻的金属，当减轻重量对设计很重要时，例如太空旅行和飞机设计，这就是一个非常有用的性质了。锂也是电池材料的绝好选择：除了重量较轻之外，它还具有很高的电化学势和较大的能量密度。

锂离子电池于 20 世纪 70 年代首次提出，并于 20 世纪 90 年代 发展起来，是最受欢迎的可充电电池之一，其可用于：

• 手机和平板电脑等移动设备
• 太阳能存储系统
• 电动汽车

锂离子电池可用于移动电话。

在将锂离子电池应用于手机和其他设备前，必须对它们进行电测试和热测试。然而，这可能很困难，因为电池通常是从第三方公司采购的，这些公司一般不会提供有关电池内部结构的详细信息，例如电极的厚度，粒径和电极材料的特定化学成分等，而电池工程师需要了解这些信息，以分析和设计电池组及其热管理系统。工程师可能感兴趣的数据包括开路电压随充电状态（SOC）的变化；传输特性（例如，扩散率和电导率）；以及不同种类的 过电位 引起的电位损失 ，包括活化，浓度和欧姆过电位。

为了设计一个可用于指定设备的电池系统，工程师可以使用集总模型，通过 COMSOL Multiphysics®软件 及其附加的 优化模块 进行参数估计，从而在给定的操作范围内提供可靠的预测。使用集总模型，当电池系统集成到设备中时，会有几个集总参数，通过这些参数可以有效地获得预测电气性能所需的信息以及进行详细的热分析。

创建集总锂离子电池模型

时变集总电池模型的参数 包括两部分：

1. 建立并求解电池的集总模型
2. 对锂离子电池的参数进行估算

电极中的传输和反应过程可以用一个集总扩散-反应方程式来描述。这就是所谓的“单粒子”模型，与传统分析模型相比，它大大减少了计算资源。诸如活化和欧姆损耗之类的其他损耗也被考虑在内。使用 集总电池 接口，您可以根据测得的充放电周期计算电池电压的变化。集总模型描述了仅使用几个集总参数就表征出质量传输，电荷转移和欧姆损耗会如何影响电池的潜在损耗。

描述用于热分析的电池的集总损耗，仅需要几个参数。

对于此示例，您可以输入实验数据以定义电池容量，开路电压，SOC 函数和电池负载。我们在对参数估算中还需要定义一些其他的参数，包括1C欧姆过电位，无量纲电荷交换电流和扩散时间常数。

在对参数进行估算的研究中，需要用到“优化模块”，此模块有各种可用于工程设计的功能。您可以使用 全局最小二乘法优化 接口来指定 一个目标 函数（该函数可估计测量值与模型结果之间的差异，因此应通过在研究中找到最佳参数值来使其最小化），同时应用 Levenberg-Marquardt 优化求解器和 “优化” 节点来指定需要优化的参数。

正如前面提到的，与使用其他模型相比，使用这种建模方法，您可以在更短的时间内估算出电池的未知参数值，而所需的计算资源却更少，同时仍可以获得可用于预测性能的模型和电池组温度设计。让我们来看一下结果。

验证参数估计的结果

从结果中，您可以看到通过电池的电压和电流，以及电池产生的电能。如下图所示，随着时间的推移（五分钟内），该模型与实验数据非常吻合。此外，在没有施加电流的情况下可确定电池的最大电压，即开路电压（OCP）。

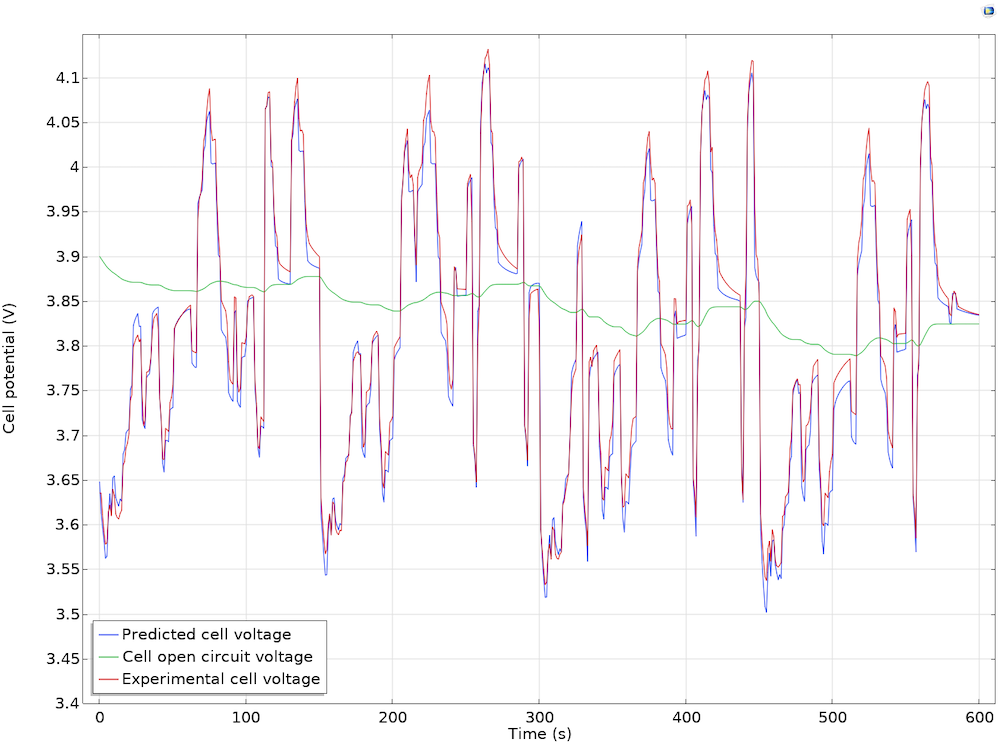
模型和实验电池的电压以及OCP建模。

该模型还可以帮助您分析过电位的影响，进一步分析电池的效率。通常，由于许多非线性和随时间变化等因素，因此很难将最小化过度的潜在问题完全解决。使用集总模型，您可以通过分析过电位（包括活化，欧姆损耗和浓度）随着时间的推移和变化的电池电流的变化情况，从而估算出电池的参数。

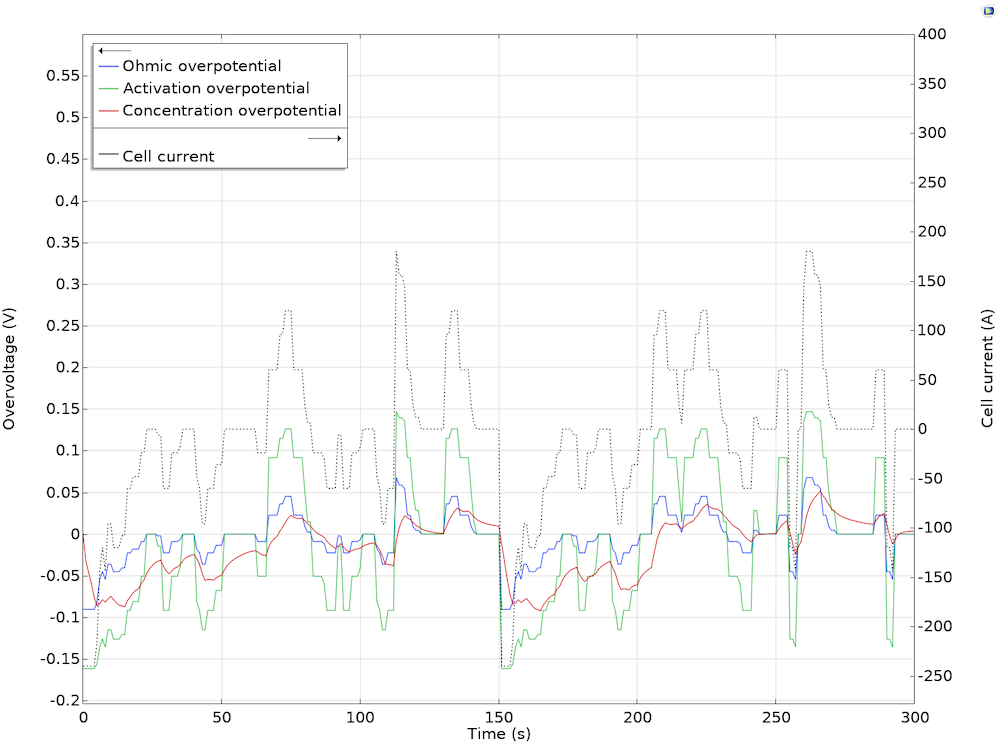
欧姆损耗、电荷转移、扩散过程在5分钟内的周期变化以及由于电池电流的变化而造成的损耗。

使用集总模型来分析，您可以获得电池组的一些相关信息，这些信息可用于电池组及其热管理系统的设计。

下一步

单击下面的按钮，从案例库中获取随时间变化的集总电池的参数估算模型。如果您具有有效的软件许可证，则可以下载相关的 MPH 文件。

进一步阅读

• 了解有关锂离子电池建模的更多信息：
  • 评估锂离子袋式电池的电极利用率
  • 如何模拟锂离子电池短路情况
• 在COMSOL博客上获取有关执行参数估计研究的更多详细信息：
  • 如何使用参数估计研究逆向建模
  • 最小二乘目标的多参数优化

锂离子（Li-ion）电池因其能效而广为人知，并逐渐成为电动汽车（EV）设计人员的首选电池。然而，这些电池的效率会随着温度的突然变化快速降低。控制温度（无论是环境温度还是电池本身产生的温度）升高的一种方法是采用液体冷却。这是一种有效的热管理方法，可以延长电池组的使用寿命。要研究电池中的液体冷却并对热管理进行优化，工程师可以使用多物理场仿真来实现。

电动汽车中锂离子电池的热管理

由于具有能量密度高，使用寿命长和自放电率低等优点,锂离子电池的应用很多。这就是为什么它在从便携式设备到电网储能等电子类应用中越来越重要。锂离子电池逐渐成为电动汽车和混合动力汽车(HEVs)的首选电池，因为它们的重量轻，但能量密度高。

尽管锂离子电池有许多优点，但它们对极端低温和极端高温特别敏感。当锂离子电池组由于环境因素或自身的充放电速率而变得过热或过冷时，其性能和使用寿命就会大大下降。不仅如此，一旦电池组在超出其最佳温度范围 20~40°C 之外被加热或冷却，即使仅仅是1°C的温度变化也可能会对电池管理系统和汽车本身的安全性、充电接受度和可靠性产生影响。

充电站处的电动汽车。图片由SanteriViinamäki提供——自己的作品。通过Wikimedia Commons在CC BY-SA 4.0下获得许可。

通过直接解决这些问题，热管理帮助设计人员重新掌握主动权。为了延长电池寿命和优化电池性能，需要关注两个与温度相关的主要因素：

1. 电池组的最佳温度范围
2. 电池组和电池内部温度均匀分布

电动汽车设计人员在设计电池热管理系统时，还必须考虑其他因素。以热管理系统的大小为例：在整个电动汽车设计中，安全电路和有害气体清除系统需要空间，并且电动汽车中的电池组必须足够大才能为整辆车供电。因此，热管理系统不能太大或太重，以免干扰电动动力系统的性能，但又需要能够快速消除较大电池组产生的热量。

什么是最有效的电池冷却系统？

通常，电动汽车中的电池通过下方式冷却：

1. 空气冷却
2. 液体冷却
3. 相变材料（PCM）冷却

尽管每种冷却方法都各有利弊，但研究表明，由于电动汽车的大小、重量和功率要求，液体冷却是电动汽车中锂离子电池的最优选择。直接液体冷却要求将电池浸没在液体中，因此，冷却液有较低（或无）电导率很重要。间接液体冷却不需要电池与液体接触，但需要使液体冷却剂在系统内的金属管中循环，这些金属需要进行腐蚀防护。

工程师可以使用 COMSOL Multiphysics® 及其附加的 电池和燃料电池模块以及传热模块，对液冷式锂离子电池组建模，来研究和优化冷却过程。

使用 COMSOL Multiphysics® 模拟液冷式锂离子电池组

本文以一个液冷式电池组为例，模拟了锂离子电池组内电池和散热片中的温度曲线。（虽然散热片可以增加系统的重量，但由于高导热性，它们对热量传递有很大帮助。）

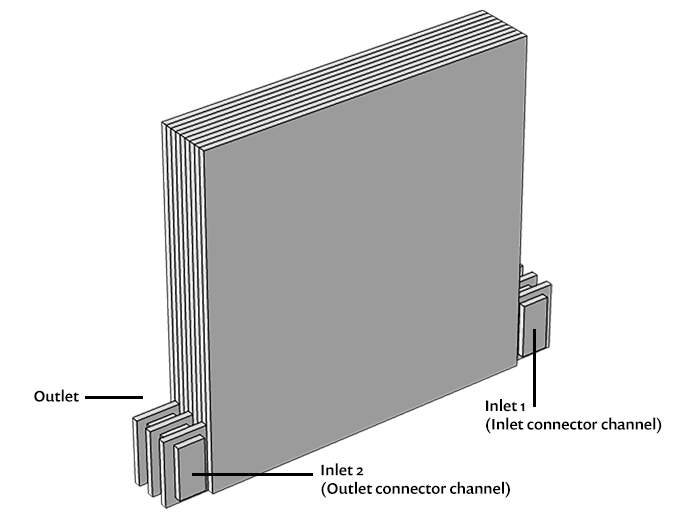
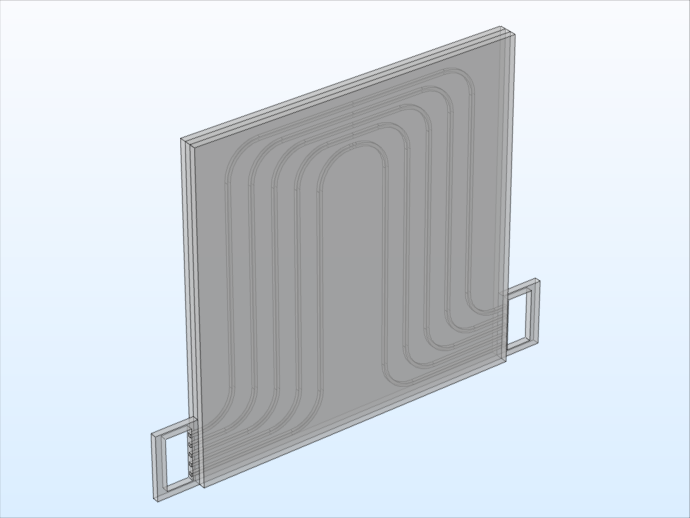
如下图所示，示例电池组的几何形状由三个堆叠的重复电池单元和两个流动连接器通道（一个在散热片的入口侧，另一个在散热片的出口侧）组成。电池组中的每个电池单元都有一个带有流道的散热片（每个厚度为 2 mm），每侧各有一个电池（每个厚度为 2 mm），总厚度为 6 mm。

左：由三个电池单元组成的电池组的几何形状。右：电池组的电池单元，带有两个电池和五个冷却通道的散热片。

建立这个模型的目的是为了在3D中求解一个负载循环内的操作点。为了计算平均热源并对电池进行模拟，我们可以使用与 圆柱形锂离子电池热建模——3D模型中相同的一维电化学模型。电池温度设置为冷却液的入口温度，放电载荷设置为 7.5 C。

假设电池组中的温度变化较小，我们可以用电池组的平均温度来计算冷却液和电池材料的性能。同样，如果在负载循环中产生的热量变化远小于电池组内的热量传递，对于给定的电池热源和工作点，可以假设负载循环中的热平衡是准稳态的并建立模型。

由于我们想要求解冷却通道中的速度和压力以及温度场，在这个模型中同时使用了层流 和传热 接口。

对于流动，假定冷却液具有水的材料属性，并且使用入口温度作为输入来计算流体属性。流过冷却板的液体在入口1进入，而早先通过电池组中的散热片的流体在入口2进入。在出口处施加大气压。

这样，传热模型就设置完成，并可以求解流动室、铝制散热片和电池的温度场问题。回到 圆柱形锂离子电池建模——3D模型，我们可以在电池域中应用相同的密度、热容量和热源。然后，在这个示例中，入口1 的冷却液温度为 310K，并对入口2施加边界热通量。类似地，在出口处施加流出条件，在其他边界处施加另一个热通量条件，来考虑在绝缘不良情况下的热量损失。

评估三个研究的模拟结果

基于物理原理设置完所有模型后，我们就可以在三个研究中按照下列顺序在物理场接口求解模型：

1. 流体流动
2. 热源
3. 准稳态温度

让我们来看一下研究结果。

对于流体流动研究，我们可以使用恒定的入口温度，以使通道中具有恒定的均匀温度和冷却流体特性。在下面的曲线图中，可以看到通道中的压力损失，这些损失可用于优化电池的流量泵。

流动室中的压力图。

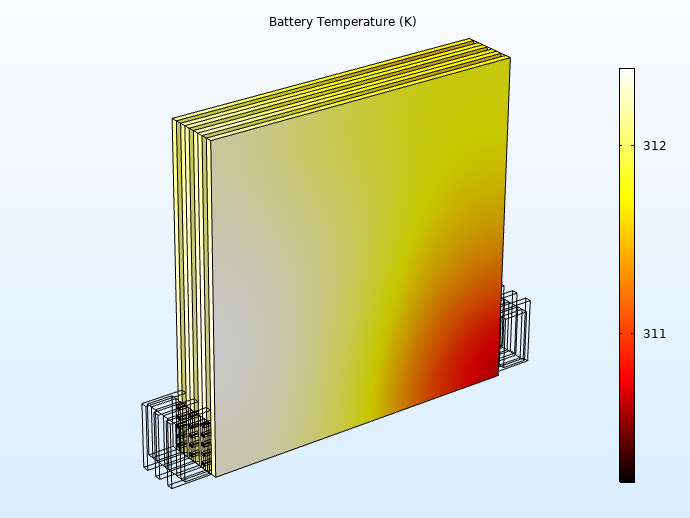
第二个研究使用瞬态研究步骤计算电池的平均热源，用于解决电化学问题。该研究预期运行时间为 60s，它假设一维电池模型中的温度恒定，等于冷却液的入口温度。左下方是电池温度，最高和最低温度之间相差约 3K。在图中，我们可以看到不同电池间的温度变化小于单个电池内的温度变化。与预期的一样，右下方的冷却液温度略低于电池中的温度，并且与整个电池组的温度分布一致。

此外，对于以下结果中第二组电池的温度，似乎散热片在此发挥了作用——面向散热片的表面温度较低，入口角落处的温度最低。

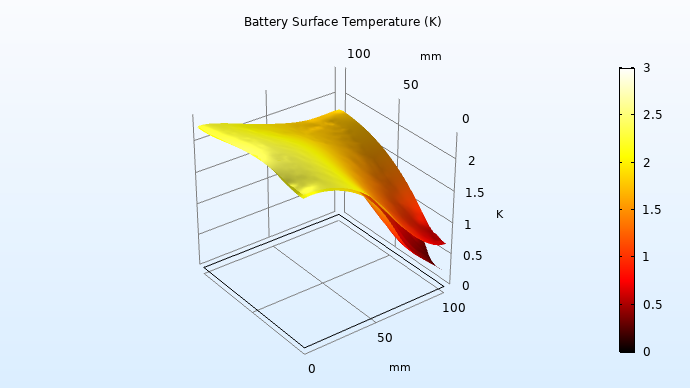
面向散热片表面和面向第三组电池表面的第二组电池的温度升高。

最后，使用第一个研究的流速和第二个研究的平均热源，准稳态研究步骤得出以下结果：通过对截面中穿过散热片中间的速度大小进行评估（如下所示），我们可以看到不同通道的流量分布是均匀的。由于总流量高，停留时间短，因此电池组在负载变化后很快达到准稳态温度。

散热片中的速度大小，显示了流量在五个通道之间均匀分布。

通过对锂离子电池组中的液体冷却过程进行瞬态和温度分析，工程师可以改善热管理并优化电池组设计。

下一步

单击下面的按钮，进入COMSOL 案例库，下载文中示例的PDF文档和 MPH 模型文件，尝试自己建立液冷式锂离子电池组模型。

如果锂离子电池的电极平衡不正确，则电池开路电压将不会准确。在本篇博客文章中，我们将介绍电极中的物质守衡以及其是如何产生的，并使用 COMSOL Multiphysics® 软件演示了一个简易电池模型。 通过该模型中使用的方法可以使电极实现平衡。此外，我们还将讨论如何将该方法用于高级建模，例如预测不同速率的充放电倍率容量并分析与电位相关的老化问题。

为什么电极平衡很重要？

电池单元由一个负极（放电过程中的阳极）和一个正极（放电过程中的阴极）组成。另外，在锂电池中，阴极上还原的锂离子的量必须等于阳极上氧化的锂原子的量。在电池工程中，平衡两侧的活性电极材料的数量至关重要。一种材料过多意味着有效地增加了电池的自重，因为如果另一种材料不能适当地平衡，则不可能 100％ 的利用该电极的活性物质。

将电池充电和放电视为在两个杯子（电极）之间来回倒入能量饮料（锂）。鉴于一开始必须先装满一个玻璃杯（平整的），如何选择每个玻璃杯的尺寸以最大程度地减少容器的总体积，同时又要最大程度地增加倒出的液体的数量（容量）和流量（流量），而不会溢出（电池老化）？

在建模方面（对于同时定义正极和负极的任何模型），电极平衡具有重要意义，因为除非适当的平衡，否则电池模型的开路电势将是不正确的。（此外，如果您的开路电势不正确，这意味着您的模型甚至在未通电流时都是不准确的。）

下面从工程角度出发，讨论如何为特定容量的电池设计电极平衡。在此讨论中，我们将使用以下定义：

• 标准电池容量：在一定的充电/放电速率下，一组指定最大和最小电压限制的电池容量
• 宿主电池容量：每个电极中可以存储锂的位点数量
• 可循环锂：在循环过程中可从电极添加或去除的可循环锂原子的数量（两个电极的总和）

电极平衡理论

正极上的可循环锂

负极（石墨、钛酸盐、硅等）材料在制造时不含锂，或未完全锂化；而正极材料（锂金属氧化物，磷酸锂等）已完全锂化。因此，原始可循环锂的量等于正极的主体容量。最初的电极平衡方法是在正极上添加所需数量的电极材料，以达到电池的标称容量，并在负极上添加相应数量的电极材料。但是，这并不容易。

选择正极容量

在正电极上，高电势可能导致不可逆的电解质氧化和气体形成，或金属离子从氧化锂基体中溶解，完全脱锂也可能破坏基体。为了延长使用寿命（或为了安全起见），电池工程师必须指定最大电极电压。

本质上，该最大值意味着降低正极的允许锂化窗口，即在电池中必须使用比标准电池容量更多的正极活性材料（建模是评估各种充电倍率下电极中电势水平的绝佳工具，但这不是本篇博客文章的研究范围）。因为在正常操作范围内，只能允许利用一部分正极容量。因此，我们不能仅基于标称电池容量研究电极平衡，我们还需要考虑对负极的有害循环效应。

增加多余的负容量

在充电即将结束时，负极达到其最低电位。负极处的低电势对电池有害，因为这可能会加速固体电解质膜（SEI）的形成，电极电势开始接近锂金属电镀的电位。

如果在电池中发生锂金属镀层，则可能导致可循环锂的额外损失，并且还导致锂金属枝晶的生长，枝晶使电池存在短路的风险。此外，由于在接近完全锂化时电极的体积膨胀系数增加，导致低电位石墨制成电极存在机械破坏问题。

较大电充电流下产生的不均匀电流分布，会进一步加剧低电位及接近100％锂化的风险（建模可以帮助评估）。因此，相对于普通电池的标准容量，负极理论容量需要适当增加。但是，这也会是事情变得更加复杂。

化成与老化

新制电池的第一次充放电循环称为“ 化成”。在形成过程中，由于寄生反应（例如产生初始SEI膜的反应）而损失了少量可循环锂。这种损耗减少了可用于充电循环的锂量。

在循环过程中，析锂也可能会与某一电极的基体紧密地结合，以至于正常的充放电循环不能再进行。同样，颗粒破裂会导致活性物质与电极的其余部分失去连接。这种现象将减少可循环材料的数量和电极容量。

通常，平衡电池时会补偿不可逆的可循环锂的损失量和形成过程中的主体容量。但是，即使可以保持良好的平衡，并通过在设备中实施循环电压约束来最大程度地减少老化寿命，也无法完全解决这些问题。随着电池的老化，可循环的锂和活性材料将不断丢失，从而导致动态的平衡问题。

电极平衡与建模

模型中准确的电极平衡的重要性不容质疑。如果热力学（即开路电势）不正确，则根本无法通过调节电导率，交换电流密度和扩散系数来补偿，这意味着电池开路电压永远不会准确，也无法平衡。

在下文中，我们将介绍用于电极平衡的数学框架，并在两个不同的示例中使用该框架。

电极平衡的数学框架

需要三个物理电荷参数来定义电池单元平衡：

1. (Ah) — 正极中的电量
2. (Ah) — 负极中的电量
3. (Ah) — 两个电极中的总电量（可用于电化学反应）

对于每个电极，电极的锂化状态（SOL）定义为

和

其中，(Ah) 和 (Ah) 分别是存储在正极和负极中的锂原子的量。
现在，我们将介绍无量纲的参数Y。这些参数通过将相应的充电参数Q（Ah）除以电池的标准容量Q _cell来实现无量纲：

为了定义电池的荷电状态（SOC），我们还需要将其中一个电极的锂化水平耦合到指定的SOC水平。

综上，需要四个参数来定义平衡模型：

1. — 正极中无量纲的电量
2. — 负极中无量纲的电量
3. — 无量纲的锂总电量
4. — SOC为0％时负极的SOL

电极的SOL可以写成下式：

上述公式用于负极

上述公式用于正极。

当使用平衡表达式时，通常需注意，电极的无量纲电量直接与SOC和锂化程度有关，具体取决于

上述表达式表明，如果给定标称电池容量，可以实现（并允许）更宽的SOL循环窗口，并且可以通过减少电极中所需的活性材料量来增加电池的能量密度。

示例1：从电池工程师的角度选择电极平衡

我们有多种方式选择四个电极平衡参数。在此示例中，从电池工程师的角度来看问题，并基于以下命题构造一个平衡：

• 在SOC为0％时，选择负极中的最小锂化水平， (1)
• 在SOC为100％时，选择正极的最小锂化水平， (1)
• 负极中所需的相对过量主机容量， (1)
• 在形成过程中可循环锂的相对损耗， (1)

 可以直接在上面的框架中使用。
此处，多余容量定义为负极中存在的额外容量，相当于0％到100％SOC之间的循环过程中获得的容量；负极中存在的额外容量，相当于100％SOC时的锂化水平与完全锂化之间的余量。可以表示为：

可以写作：

确定和 比较棘手. 在形成过程中，首先假设所有可循环锂由于在负极中形成初始SEI层而损失，并且该容量损失与 成正比。 因此，

可以写作：

其次，我们使用SOC为100％的 和 或更高 时的公式来与其他参数相关：

和 的表达式可重新排列为:

示例2：使用COMSOL Multiphysics®对电极平衡进行反向设计

如引言和第一个示例所示，为了在模型中构建正确的电极平衡，需要大量的信息。如果任一参数有任何错误，则模型的开路电压可能会与实际电池的开路电压不同。商用电池（您尚未自己制造）的另一个问题是，可能根本不知道所需的参数。

在此示例中，我们将从电池的实验性开路电压和一些基本假设出发，使用反向设计方法作为电极平衡的替代方法，然后通过优化求解器找到合适的电极平衡。

电池的实验开路电压如下图所示。在这种情况下，当开路电压由3.0 V变为4.15 V时，电池SOC由0变为1。

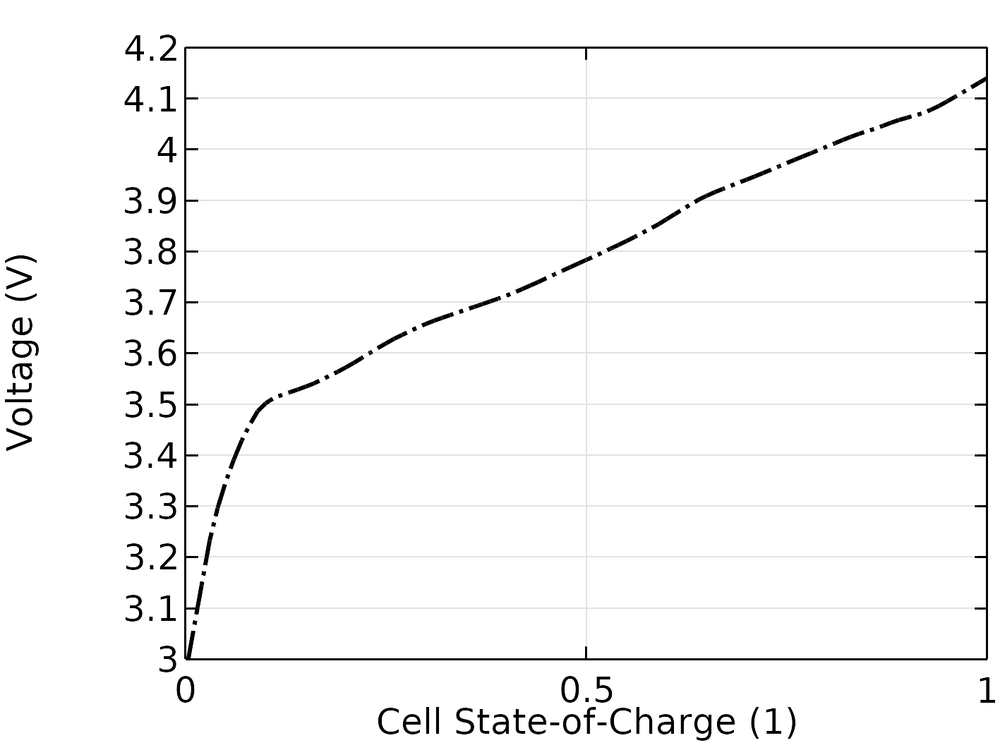
实测开路电压与电池SOC的关系。

假定该电池为（1：1：1）LiNiMnCo（NMC）-石墨电池。为了构建电池开路电势，我们使用了电池和燃料电池模块（COMSOL Multiphysics的一个附加模块）材料库中电极材料的平衡电位曲线。这些曲线基于实验的半电池数据，并表示为平衡电位E _eq（V）的插值函数，它是锂化状态（SOL）的函数，如下所示。

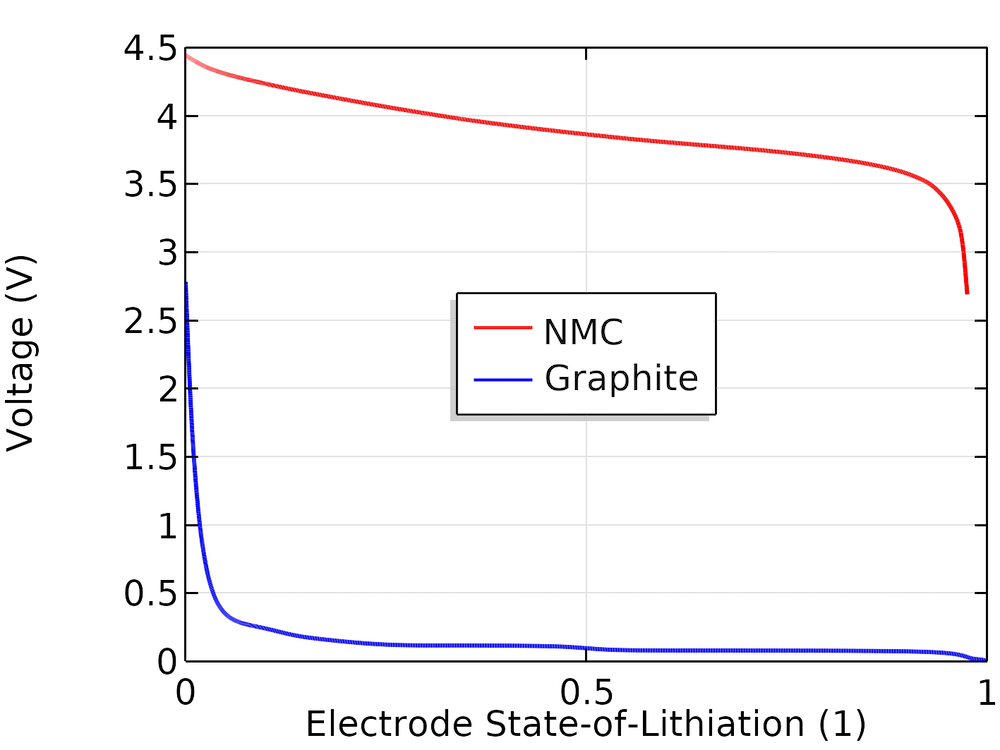
平衡电极电位与SOL的关系

使用上面的数学框架，将电池开路电势构造为正负开路电压之差：

在使用优化解算器的过程中，利用COMSOL Multiphysics软件执行四个拟合参数的参数估计 (, ,,和 )

对于实验开路电位（OCP）曲线与SOC的所有数据点，使用最小二乘方法和最小化目标函数，将ø 定义为：

结果与讨论

实验和建模的电池电压与电池SOC的关系以及各个电极的电压值如下所示。可以看到，对于该特定电池，半电池曲线与真实的实验电池OCP吻合。

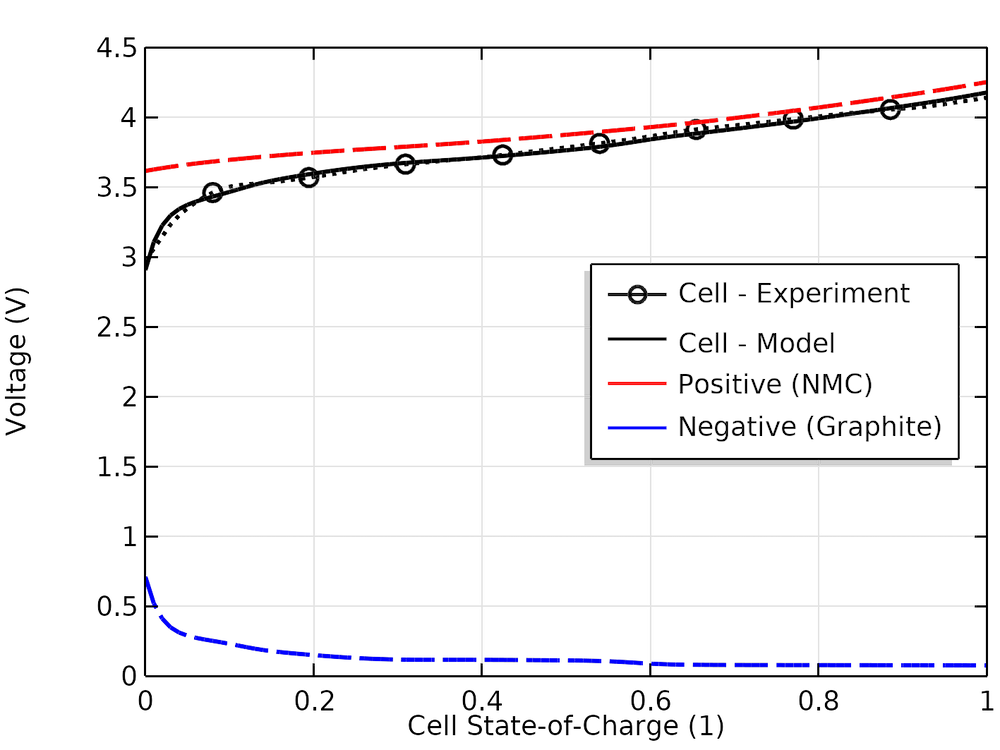
电池开路电压的实测值、模拟值与SOC的关系，以及相关的正负电极电压。

下表为拟合的参数值。术语 高于1，表示在单元OCP曲线的电压窗口内循环时未使用所有容量。类似地， 高于1，表示在负极大约有25％的剩余容量，以便在充电过程中相对于析锂具有潜在的余量。（参见示例1中 的定义)我们还注意到， 比小10%, 得到锂形成过程中损失的量的量度 (参见 定义1中 的示例).

参数	拟合值
	1.27
	1.22
	1.14
	0.025

下图显示了电池电压和相应的SOL值随电池SOC的变化，表示在拟合模型中，当电极在0％至100％电池SOC之间循环时，电极的实际SOL循环窗口。

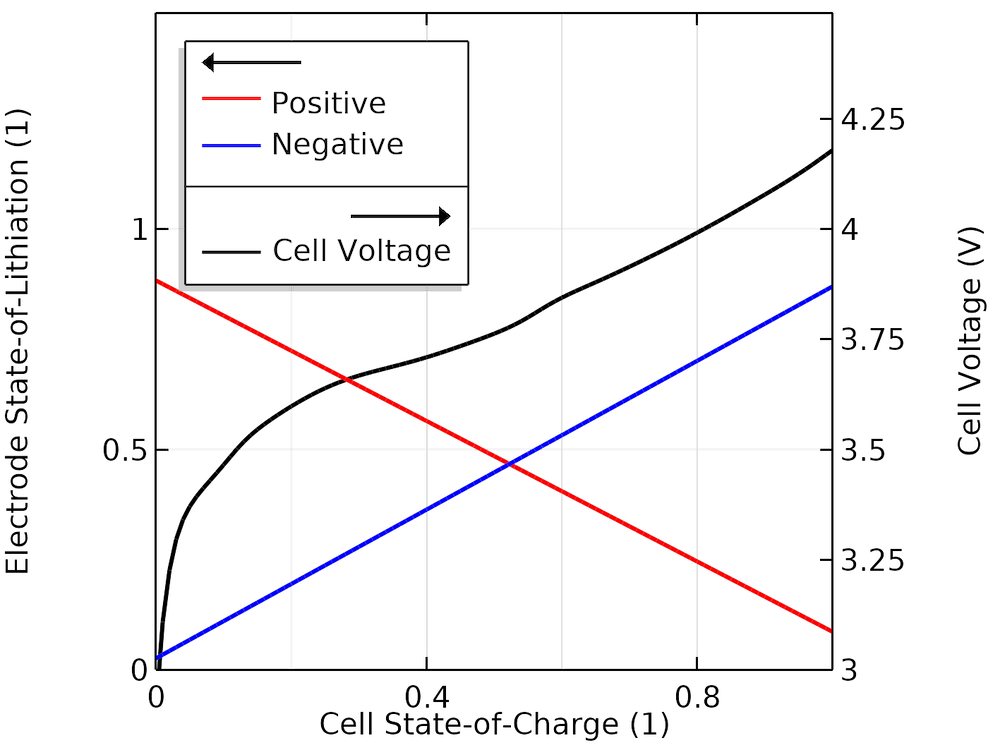
每个电极中拟合的SOL与SOC的关系。

毫无疑问，上述拟合方法可用于模型中并获得适当的电极平衡。但是，它也可以直接分析电池的老化（健康状态）。假设半电池平衡电势曲线相对于SOL的形状对于老化电池没有变化，我们可以随时执行上述拟合过程以监控电池的健康状态。拟合值的变化, , 或 ，则对应于可循环的锂和/或基质材料的损失。我们可以将其视为常用dVdQ方法的补充方法，在该方法中，将分析开路电压与SOC曲线导数中的峰值位置。

使用电池平衡参数进行高级建模

现在可以使用四个电极平衡参数中的任何一组来构建更高级的模型。例如，用于预测不同速率下的充放电容量的性能建模，或某些与电位相关的老化反应的详细建模。
例如，上面的参数将对应于COMSOL Multiphysics中锂离子电池界面中的下列表达式

和

其中，积分分别取自正极和负极域。在此， 是电极的孔隙率， (mol/m³) 是嵌入的锂的最大浓度。即电极相的体积主体理论容量。

假设每个电极中的电极特性都是恒定的，则可以按如下方式设置电极体积分数：

和

其中, (m) 和 是每个电极的厚度， (m²) 是电极平面的面积。
其余两个参数与电极中嵌入的锂浓度的初始值有关。在多孔电极模型中，锂化的局部状态定义为：

其中， 为嵌入锂的局部浓度。
因此，初始浓度的表达式可以从上述SOL _neg和SOL _pos的表达式中得出。例如，将初始浓度设置为与上述的0％电池对应的SOC。

在负极域；

在正极域。

下一步

要了解“电池与燃料电池”模块中电池建模的特性和功能，请单击以下按钮：

扩展阅读

在这些博客文章中了解有关锂离子电池建模的更多信息：

• 如何为锂离子电池短路建模
• 锂离子电池：纽曼模型的异构替代品
• 评估锂离子电池袋式电池的电极利用率