特征模态和重叠积分

小测验：为下一代通信系统设计光缆，优化桥梁设计以尽量减少不必要的机械共振和优化客厅的声学布局，这三者有什么共同之处？

对于上述每一个场景，我们都必须充分了解系统的特征模态。特征模态及其相关特征值（也称为固有频率）描述了线性系统对外部激励的响应方式，因此在设计中起着至关重要的作用。在一些应用中，例如射频通信腔滤波器或扬声器驱动器，我们希望能最大程度地耦合一个或多个特征模态，而在其他应用中，这些共振模态的耦合可能会导致灾难性后果，如桥梁坍塌。

当在参数扫描过程中调整系统参数，如工作频率或几何尺寸时，特征模态和频率自然会发生变化。然而，这些模态通常会保持定性相似性。让我们来看一个简单的示例，像鼓或克拉尼板振动表面一样的二维椭圆形薄膜的波动方程。

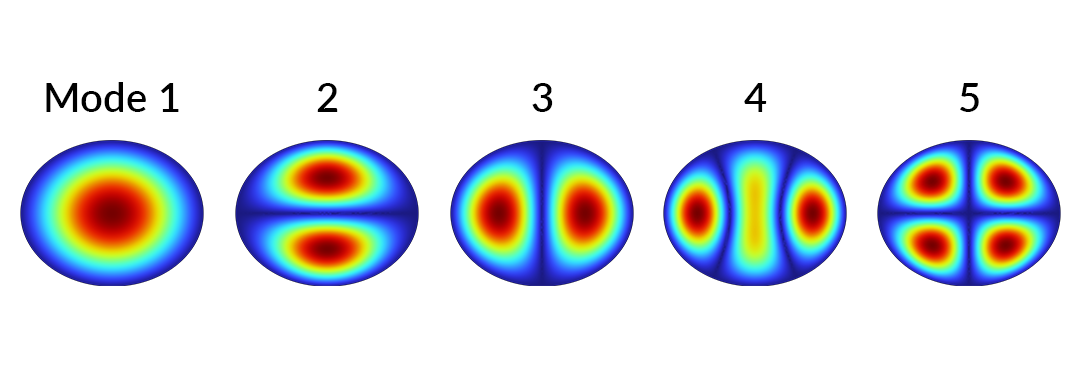
具有固定边界的椭圆形薄膜的二维波动方程的前 5 个特征模态解。

特征频率研究显示了前 5 个特征模态，其位移大小如上图所示。现在，假设我们要对椭圆域的垂直高度进行参数扫描。

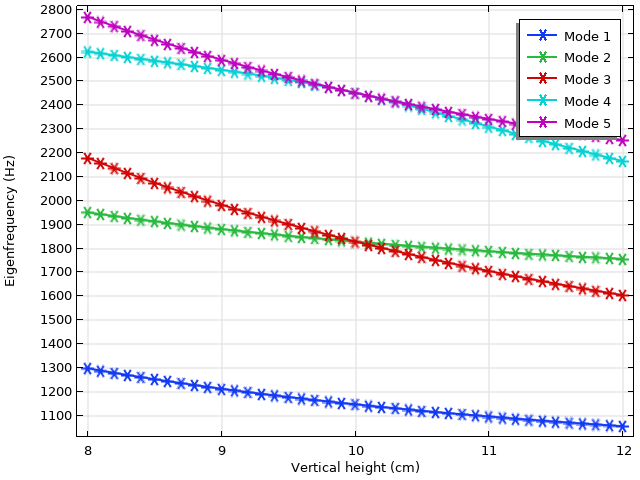
图中显示了前 5 个模态的特征频率与椭圆域垂直高度的关系。请注意，在高度为 10 cm 时，模态 2 和模态 3 ，模态 4 和模态 5 之间的简并，而此时椭圆域是圆形的。

前 5 个模态的特征频率如上图所示。请注意，当垂直高度为 10 cm 时，模型域是圆形的。这导致模态 2 和 3 之间，模态 4 和 5 之间的简并。事实上，过了简并点，模态 2 和 3 就会在特征值图中互换阶次。这种模态交叉行为在许多特征频率研究中都很常见。当这些模态的阶次发生变化时，如何在特征值图中追踪它们呢？要回答这个问题，让我们仔细观察其中的一个模态。

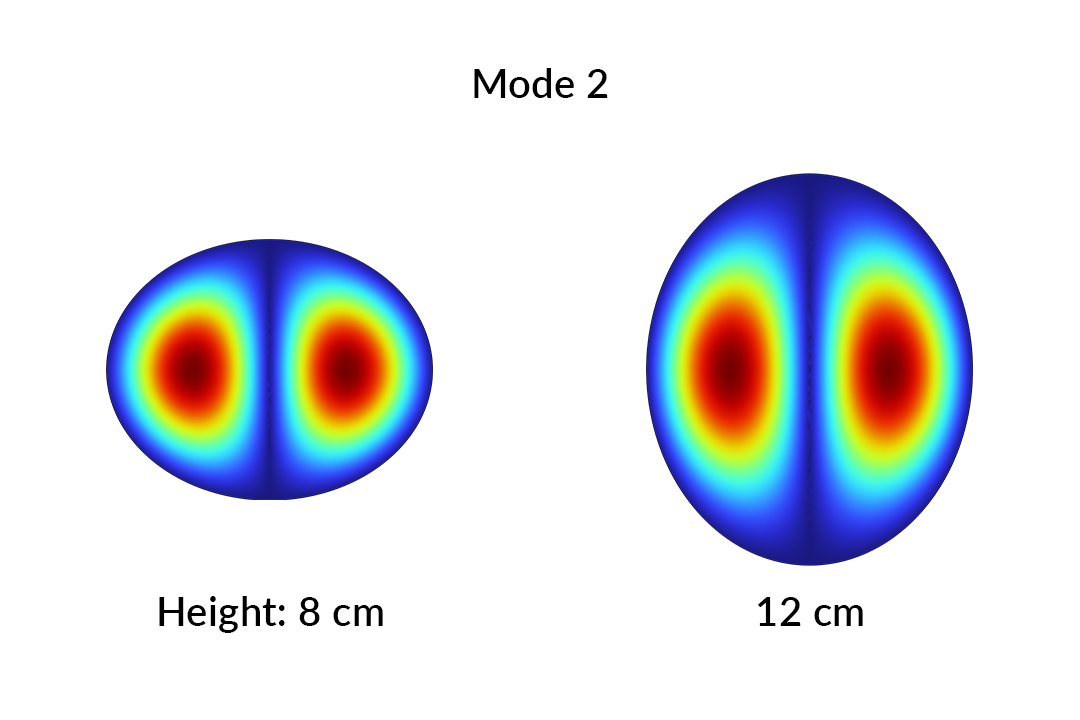
参数范围两个端点处的模态 2。

高度为 8 cm 和高度为 12 cm 时的模态 2 如上图所示。通过肉眼就可以明显观察到这两个模态的相似性。我们可以用模态重叠积分来量化这种相似性：

变量 和 代表两个任意的特征模态解。这个方程的关键部分在于分子：在两种模态之间进行 内积 。分母将重叠度的值归一化，使其介于 0 和 1 之间。

一个模态与其自身的重叠度为 0，因为它们是相互正交的。对于参数值不同的模态，只要模态在性质上相似，M 接近 1。例如，上述两个模态的重叠度 M = 0.95，证实了我们的直观识别。两个不相似的模态的重叠度接近 0。

利用这一度量标准，我们可以通过对重叠值施加一定的阈值，来建立模态匹配方案。这可用于色散图中过滤或分组模态，甚至在模型方法的帮助下自动生成模态轮廓动画。接下来，让我们看看如何将这一策略应用到多个不同的物理学科。

示例 1：光学各向异性波导

在上一篇关于如何模拟光学各向异性介质的博客中，我们研究了光学各向异性波导的横向模式。这些模式可以按照电场的主要方向以及横向平面上振幅最大值的数量进行分组。 模式的一些示例如下图所示。

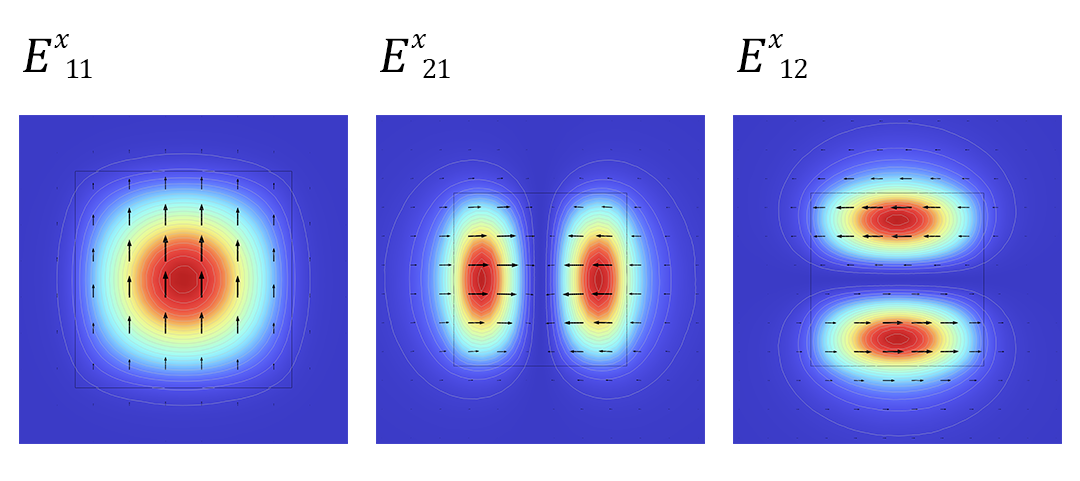
光学各向异性波导中前 3 个 特征模式。

由于波导的主要目标是控制光流，因此了解这些传播模式的行为至关重要。在每个频率下，每个模式都有一个相关的有效折射率，该折射率决定了它们的传播速度、有效波长以及衰减程度（如果模型中存在损耗）。我们使用色散图来绘制有效折射率随频率变化的曲线。

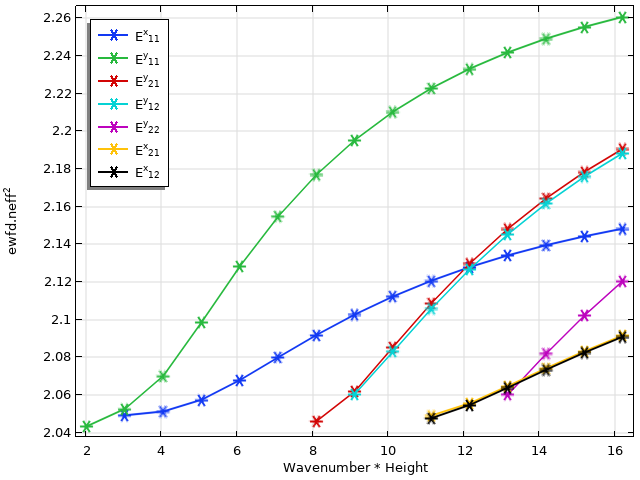
波导的色散图如上所示。由于存在大量的模式交叉，因此有必要对特征模式进行分类，以便正确标记。

在模式分析研究的原始输出中，没有以任何有意义的方式有效折射率进行分组或排序，因为求解器没有这些模式的先验知识。我们采用重叠积分计算方法，按模态轮廓对这些特征值进行分类。现在，由于每个有效指数值都与特定的 或 模式相关联，因此我们可以轻松地使用滤波器和绘图选项在绘图图例中为每个模式着色和标注。请注意，这种方法能够正确解析多模式交叉以及特征值非常接近的模式，例如 和 模式的交叉。

示例 2：旋转叶片的特征频率

深入理解风力涡轮机叶片或电动汽车电机等旋转部件的共振模态，对于稳定性分析或最大限度减少噪声和振动等应用至关重要。我们来看 COMSOL应用库中的一个基本示例：旋转叶片的基本特征频率模型 。

当矩形叶片以越来越大的角速度旋转时，预计会出现两种主要的竞争现象：应力刚化和旋转软化。前者由于离心效应产生的静态应力场使叶片变硬，从而对固有频率产生向上的影响。后者则由于运动的径向放大而使叶片软化，导致对固有频率的向下影响。这些效应的平衡在坎贝尔图中得到了最好的体现，即固有频率与旋转角速度的关系图。

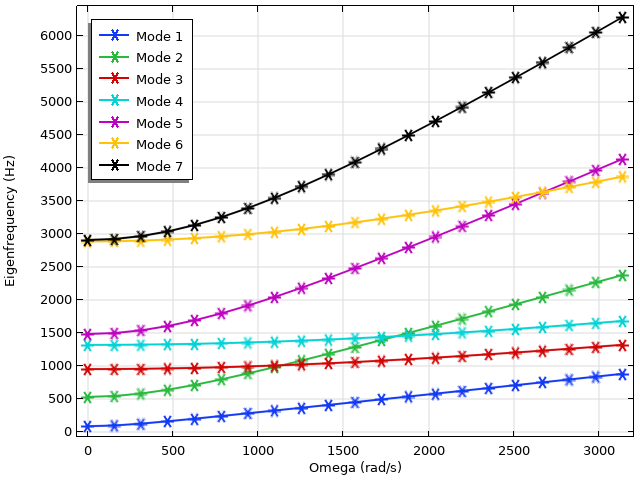
旋转叶片的坎贝尔曲线图。请注意，模态 2 和 5 的特征频率明显增加。

上图是前 7 个特征模态的坎贝尔曲线图。总体而言，我们观察到固有频率呈上升趋势，这表明应力刚化起了很大作用。这在模态 2 和 5 中更为明显，在所研究的参数范围内，这两个模态的特征值急剧上升，并超过了其他模态的特征值。前 6 个模态的位移和应力如下图所示。

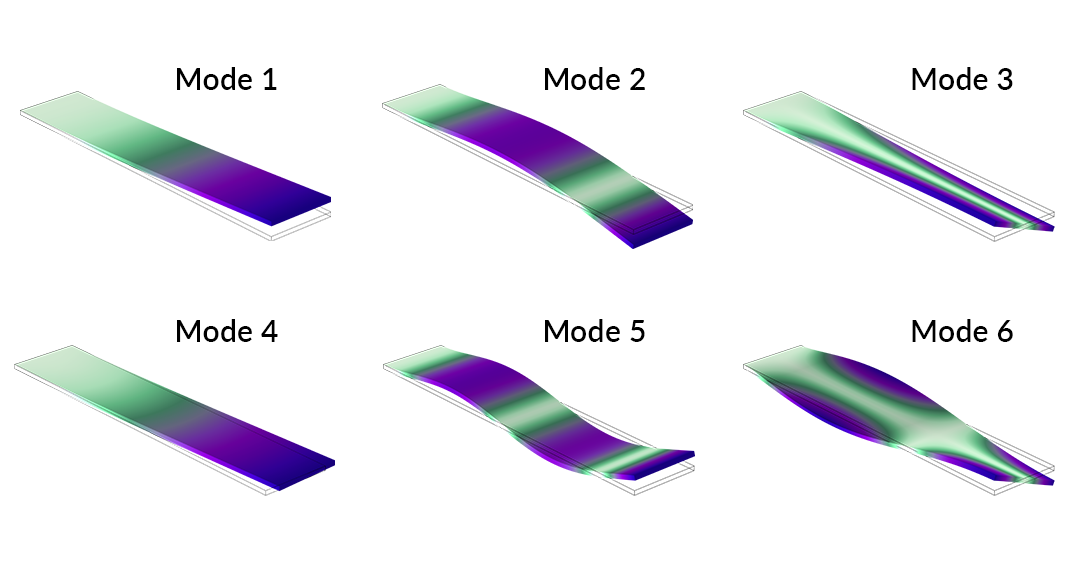
旋转叶片的前 6 个特征模态。

在更复杂的系统中，坎贝尔图中的固有频率可能更多，既有上升趋势，也有下降趋势。了解这些趋势并将其可视化，对于确定如临界转速等至关重要。通过模态重叠积分，可以轻松地对这些模态集的行为进行分类和追踪。

示例 3：带弹性壁的消声器特征模式

多物理场仿真在内燃机消声器的设计中发挥重要作用。除了模拟空气中的压力波外，还必须考虑空气与消声器外壳之间的相互作用，从而可以更加准确地模拟整个频率范围内的传输曲线。

声-结构相互作用的其中一种效应是引入更多的共振模式，这一点可以通过两个相关的示例来说明：消声器中的特征模式 和 带弹性壁消声器中的特征模式。我们来详细探讨后一个模型。在一定频率范围内对消声器横截面进行模式分析，以确定模式轮廓及其相应的截止频率。

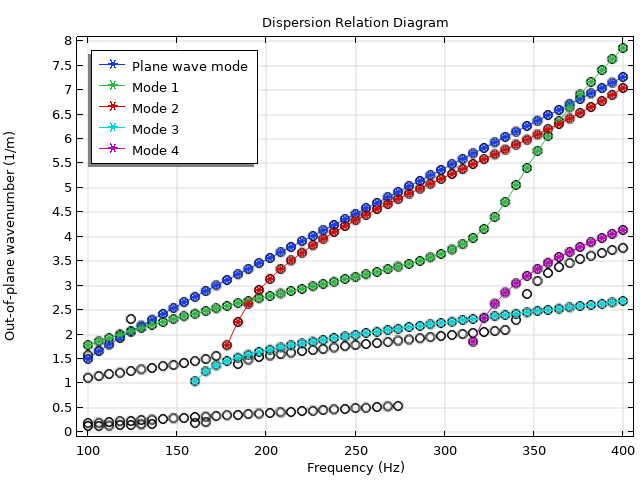
带弹性壁的消声器色散图。除平面波模式（蓝色）外，由于空气与消声器壁之间的声-结构相互作用，还存在许多其他模式集。使用模式重叠积分法跟踪了其中的一个子集。

上面的色散图绘制了部分模式及其传播常数与频率的关系。显然，数据集中的趋势很可能与不同的模式系列相对应。例如，平面波模式形成了一条贯穿整个频率范围的对角直线。通过应用重叠积分，我们可以确认平面波模式的预期行为，并追踪整个频率范围内的其他几个模式。模式轮廓图如下所示。

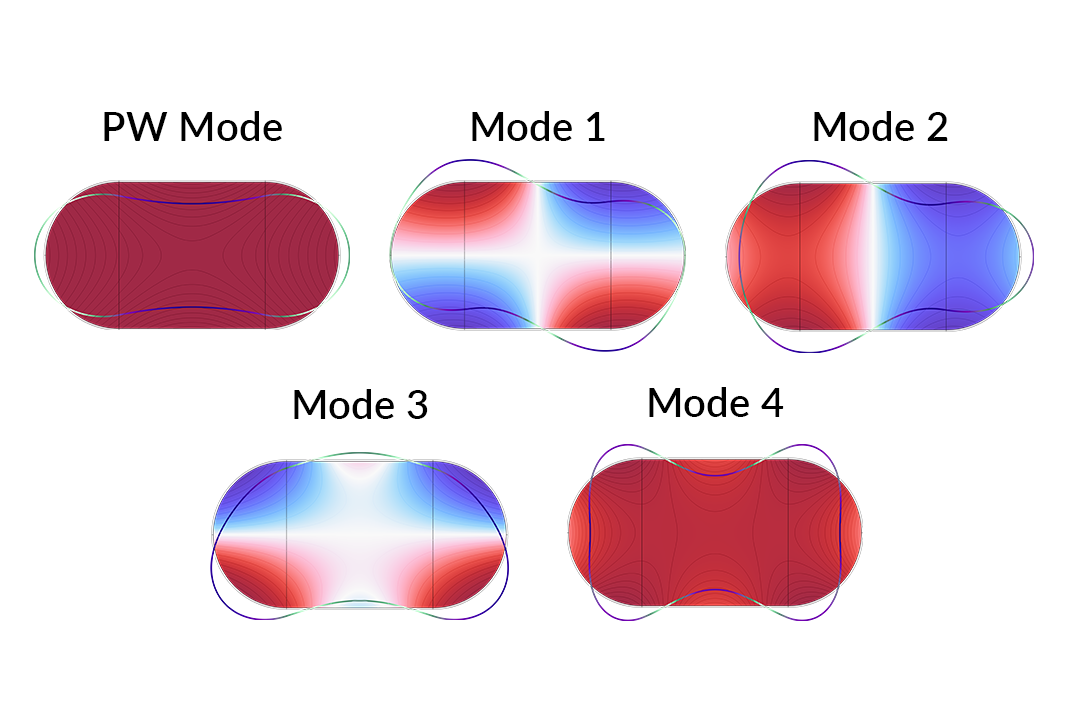
上图显示了带弹性壁的消声器中的部分模式轮廓。

借助模型方法，我们甚至可以自动生成整个频率范围内的模式演变动画。

在模型方法的帮助下，在整个参数范围内对模式 3 的演变进行追踪并用动画演示。

上面的动画演示了模式 3 如何从接近其截止点的 160 Hz 急剧变化到研究的上限 400 Hz，过程中还跨越了其他几个特征模式。在模态重叠积分的帮助下，追踪单个模式集的演变变得更加容易。

下一步

在这篇博客中，我们演示了如何使用模态重叠积分方法在特征频率研究中追踪和分类模态。请点击下面的按钮进入 COMSOL 学习中心，了解相关内容：

此外，这篇博客中讨论的模型可在 COMSOL 案例库中下载：

• 各向异性光学波导
  
• 旋转叶片的基频
  
• 带弹性壁的消声器中的特征模态
  

扩展阅读

• 下一代红外光纤设计的仿真分析
• 通过形状和拓扑优化实现特征频率最大化
  
• 室内设计声学
• 多物理场仿真优化消声器设计
  

静电放电器件损伤的类型

静电放电事件最常见且最明显的例子就是闪电，但并不是所有静电放电事件都会产生明显的火花。物体上积累的静电电荷量取决于其材料、表面积和周围环境的相对湿度。静电放电也可能由静电感应引起，当带电物体在远离地面的导电物体周围产生静电场时，就会发生静电放电。

图 1 有明显火花的静电放电事件。照片由 P. Mikołajek 拍摄，通过 Wikimedia Commons，遵循 Attribution-Sharealike 4.0 国际许可协议。

这些静电放电可释放几伏到几千伏的电压；然而，无论是简单二极管还是复杂集成电路电子元件,即使是低压放电也可能对电子元器件造成严重损伤。（一个人身上携带的电荷足以对电子器件和元件的性能造成损伤，从而导致数据丢失、文件损坏和系统崩溃！）因此，在这些器件的制造、组装和运输过程中,以及对于成品器件而言，预防静电放电事件都非常重要。

理解和预防静电损伤

为避免静电放电事件对电子器件和系统造成损伤，必须对元件、印刷电路板和系统各个层面进行各种测试。然而，这些测试只能在元件或系统制造完成后才能提供帮助。COMSOL Multiphysics^® 软件能够帮助工程师在设计阶段发现静电放电问题，同时还能提供有关电磁场分布的详细信息，从而准确测试。这些知识对于理解静电放电损伤发生的原因以及如何修复损伤至关重要。

静电放电事件可能导致芯片绝缘故障或逻辑错误。当本应处于低电平状态（0）的引脚在超过 1 ns 的时间内承受振幅高于 1.5 V 的电压，或在超过 5 ns 的时间内承受振幅高于 0.3 V 的电压时，就会发生逻辑错误，从而导致引脚错误地转入高电平状态（1）。

接下来，让我们来看看静电放电如何导致印刷电路板上的微芯片出现逻辑错误。

模拟电路板中的静电放电

RF 模块是 COMSOL Multiphysics^® 的附加产品，包括用于静电放电电流研究的物理场接口。静电放电电流通常是非线性的，需要进行三维瞬态分析。电磁波、瞬态 接口包括四个预定义的静电放电电流，用于满足不同的测试标准，并支持预定义和参数化的时间脉冲函数，这些函数常用于描述静电放电和闪电。工程师可以在运行仿真前即刻绘制脉冲形状，以确保所选函数参数合适，方便检查。

在示例的模型中，静电放电电流是使用 集总端口 功能和扩展的人体模型（HBM）标准生成的，以测试极端条件下的性能（图2）。

图 2 基于扩展的人体放电模型的静电放电电流。

请注意，我们不会在此介绍如何设置该模型的细节，欢迎点击文末链接下载此模型的 MPH 文件和相关说明。

仿真结果

模型计算了微芯片上两个引脚（1、2）的感应电压，以评估静电放电是否会导致误差。下图左侧显示了 t = 1.2 ns 时静电放电电流引起的表面电流密度，右侧显示了通过仿真计算的芯片的两个引脚（1、2）上的感应电压。

图 3 微芯片上两个引脚处的感应表面电流和电压。图中添加了一个虚拟的手指供参考。

可以看出，引脚 2 上的感应电压振幅高于 1.5 V，极有可能导致逻辑错误。

表面电流密度的模随时间变化，以对数刻度显示。

预防静电放电损伤的策略

静电放电是一种常见现象，也是导致电子器件损坏和故障的主要原因。随着器件尺寸的不断缩小和电路密度的持续增加，制造商越来越需要密切关注静电放电损伤的预防。

数值仿真提供了一种深入理解这些微型器件的方法，以及在需要建立物理原型之前准确模拟和优化设计的方法。它还可以作为一种预兼容测试，对各种测试进行有效补充。仿真测试的通过可以高度增强设计人员对物理实验的信心。仿真还可以帮助探究故障机理和电流分布，并提供有效的解决方案。

下一步

想尝试自己动手模拟文中示例的静电放电模型吗？您可从 COMSOL 案例库中下载包括分步说明在内的所有模型文件。

仿真场景：非线性变压器

在上一篇使用 COMSOL Multiphysics^® 计算增量电感的博客中，我们探讨了一个由缠绕在非线性磁芯材料上的两个线圈组成的变压器示例。当外加正弦交流电压时，初级线圈和次级线圈会产生感应电流。但是，当电流足够大时，材料的非线性将显著改变增量电感，从而产生非正弦感应电流。我们可以通过建立变压器的全保真模型，或建立考虑了非线性增量电感的等效电路模型来模拟这种行为。非线性使电流随时间呈非正弦周期性变化，我们可以运行瞬态模型多个周期来观察这种逐渐降低到稳定状态的变化。

由缠绕在非线性磁芯上的两个线圈组成的变压器。从有限元模型中提取增量电感，用于等效电路模型中。

运行等效电路模型多个周期后的结果，周期性信号的幅值逐渐接近稳定。

从结果来看，很显然需要模拟多个周期。如果我们只对时间周期稳态解感兴趣，那么大部分生成的数据实际上是不需要的。理论上，在这种情况下我们需要一种能直接获得时间周期解的方法，这正是本文要讨论的内容。

从时间到空间重写等效电路

如果仔细观察该电路模型，我们会发现它只有两个随时间变化的未知数：和 , 即通过初级线圈和次级线圈的电流。现在，让我们从电路的范式来思考问题，考虑两个电流回路中各个元件的压降，用以下方程表示

其中，所有增量电感都是两个电流的函数： 。这组耦合常微分方程可以用多种方法求解。我们仅求解外加电压为 ，以及方程解的周期为 的情况。

很明显可以看出，除了电流的时间导数，这几乎是一组非线性代数方程。但如果用空间导数来代替时间导数呢？让我们看看会发生什么！

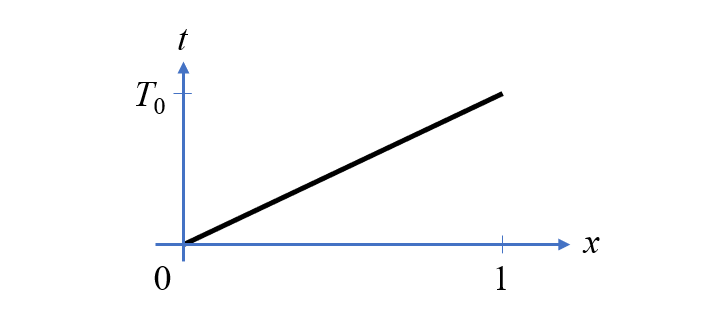
沿一维单元域绘制的时间与位置的函数。

考虑一个一维域，即一条单位长度的直线。定义一个沿长度线性变化的准时间变量。如果在这条直线上定义两个与空间相关的因变量 和 ，并引入网格，那么 COMSOL Multiphysics^® 软件就可以通过微分算子： d(u1,x) 求空间导数。但由于我们将空间维度视为时间维度，因此这实际上是求时间导数。鉴于此，现在可以用 域常微分和微分代数方程 接口构建一个定义在单位长度直线上的场代数方程。该接口的软件界面截图如下图所示，其中定义了两个未知数。使用拉格朗日单元划分这些场，这会自动确保场的连续性，然后，需要给场和源设置合适的单位。为了便于阅读，还可以定义一组变量来描述电路模型中每个元件所产生的压降，如下图所示。

域常微分和微分代数方程 接口设置，包括设置场变量名称、选择形状函数和设置单位。

定义了时间空间的外加电压、电流导数以及电路各元件上的压降的变量。

我们将在 域常微分和微分代数方程 接口的 代数方程 特征使用这些变量，该接口包含两个编辑框，需要输入必须始终等于零的方程。在这个示例中，我们输入两个电流回路的电压降项和源项，也就是上文中列出的方程。最后，在域终端的一个点添加两个逐点约束。此处是通过 积分 特征，在另一个点上定义的约束 u1-intop1(u1) 和 u2-intop1(u2)，来实现周期性边界条件。

在单位域输入时间空间的代数方程。

通过 逐点约束 和 积分 特征定义周期性边界条件。

当变压器进入非线性状态时，要求解这个稳态问题，需要在域上设置相对较细的网格。因此，在求解这种非线性稳态模型时，求解域上网格的尺寸是需要测试的参数。稳态模拟结果如下图所示，将其与瞬态结果进行比较，结果显示二者非常吻合。事实上，当以更严格的容差求解瞬态模型时，二者之间的差异就越小。但即使是这样一个小模型，高精度的计算都会显著增加瞬态计算的成本，而稳态计算几乎可以瞬间求解。

电路模型计算出的瞬态结果与使用时间周期方法计算的稳态结果的对比。

通过空间 FFT 数据集 特征，我们还能使用空间中一个周期的解提取频率组成。该特征的设置如下图所示，其中突出显示了一维阵列 数据集，该数据集会对计算结果进行周期性扩展，使结果看起来更加平滑。通过绘制适当归一化处理的量，我们可以看到频率组成如何随着外加电压的增加而增加。

空间 FFT 数据集将一维阵列数据集作为输入，周期性的对稳态计算结果进行拓展。

交流电压升高时的频率组成。

结束语

这篇博客，我们介绍了一种特别高效的方法，求解用一组代数方程描述的系统的周期性稳定解。需要注意的是，只要存在平滑的周期性解，这种方法就可以使用任何类型的应用信号，而不仅仅是正弦强制函数。此方法设置非常简单，并且利用了 COMSOL Multiphysics^® 的核心功能，因此适用于任何类型的问题，而不仅是电路问题。对于使用COMSOL 的仿真人员来说，这是一项非常有用的仿真技术。

您可以点击下方按钮，下载相关示例模型：

编者注：这篇博客最初发布于 2016 年 7 月 4 日。现已更新，以反映软件的后处理新功能。

2 种 RF 仿真方法简介

在今天的博客中，我们将讨论 2 种仿真方法：渐近波形估计（AWE）法和频域模态（FDM）方法。这两种方法都旨在帮助用户解决采用超精细频率分辨率，或通过常规的 频域 研究运行超宽带仿真时，求解时间过长这一常见问题。当涉及描述具有单一谐振或无谐振的平滑频率响应时，AWE 方法非常有效。而 FDM 方法则适用于快速分析多级滤波器，或者目标通带内有多个谐振的大量元件的滤波器。接下来，我们将讨论这两种方法的典型设置和应用场景。

需要说明的是，AWE 和 FDM 方法几乎都不依赖于所选的频率步长。您可以自由地减小频率步长的值，获得分辨率良好的结果绘图，而不会出现明显的速度减慢或额外的内存消耗。不过，这种做法也存在缺点：降低频率步长值可能会影响最终解中保存的数据量。在本文末尾的数据管理部分，我们将给出能显著减小输出文件大小的建议。

请注意，在使用精细分辨率进行 AWE 或 FDM 计算之前，最好先使用较粗的频率分辨率运行一个初步的 特征频率 和常规的 频域 仿真。这可以帮助您快速地估算谐振位置，总体了解系统的频率趋势，包括实际通带和所需的频率分辨率。

AWE 方法促进降阶模拟

AWE 是一种先进的降阶模拟技术，由于其数值特征和数学算法技术性太强，我们在此不过多赘述，只演示如何在 RF 模块中使用此方法。 自 COMSOL Multiphysics 6.2 版本开始，软件新增了有一个专门的 自适应频率扫描 研究步骤，可以实现 AWE 方法。使用此功能时，需要指定目标输出的频率范围，并选择一个表达式用于对AWE 算法进行误差估计。该方法求解器可执行快速频率自适应扫描，默认情况下，使用 Padé 近似。

自适应频率扫描 研究设置。使用查看默认的 渐近波形估计（ AWE） 表达式。

在模拟谐振电路，尤其是包含许多频率点的带通滤波器类器件时，AWE方法非常有用。例如，COMSOL 案例库中的消失模圆柱腔滤波器模型先运行了一个常规的 频域研究，以 5 MHz 的频率步长对 3.45 GHz 到 3.61 GHz 之间的仿真频率进行初始扫频。

消失模圆柱腔滤波器教程模型 (左) 及其离散频率扫描结果 (右)。谐振频率附近的 S 参数图看起来并不平滑。

假设以更高的频率分辨率再次运行仿真，例如使用100 kHz的频率步长进行扫描，即分辨率提高 50 倍。可以预计，完成仿真所需的时长将提升50倍。但是，在此特定的示例中，使用 自适应频率 扫描研究完成仿真所需的时长几乎与频率扫描仿真所需的相同，并且能获得以100 kHz 频率步长计算的所有因变量解。

求解时间可能会在一定程度上受用户输入的 AWE 表达式的影响。任何模型变量都可以作为 AWE 表达式，只要能生成一个平滑的结果图，如高斯脉冲或平滑的曲线作为频率的函数，但最明显和典型的选择是基于s参数的全局表达式。例如，对于双端口带通滤波器，将S21 的绝对值 （abs(comp1.emw.S21)） 作为 AWE 表达式的输入可以获得非常好的结果。如果 AWE 表达式的频率响应包含无限梯度，例如在单个频率点具有良好阻抗匹配的天线的S11值，完成仿真则需要更长的时间。如果天线损耗可以忽略不计，使用 sqrt(1-abs(comp1.emw.S11)^2) 表达式可能结果更好，且能缩短计算时间。上述表达式是默认的 物理场控制 选项的 渐近波形评估 (AWE) 表达式。作为合理的检查方式，我们始终可以先以较粗的分辨率运行一个频域 扫描，绘制表达式，并选择最平滑的结果。

开始运行 自适应频率 扫描前，需要在研究中设置所需的更精细的频率步长。当仿真完成后，模拟所需时长几乎与离散频率扫描的相同。对比求解出的S参数。由于AWE求解器运行的频率扫描分辨率提高了50倍，因此其频率响应（S参数）结果绘图看起来也更平滑。使用这种方法，不仅可以节省宝贵的时间，还可以获得准确且出色的结果，而且谐振频率的定位也更加准确，如下图所示。如果您对此感兴趣，可以使用相同的分辨率运行一次常规扫描来进行验证，并检查结果是否一致。

分别运行 自适应频率 (AWE) 和离散 频域仿真 计算出的 S 参数图。使用 AWE 方法模拟的结果绘图的分辨率提高了 50 倍。

使用频域模态方法模拟电路谐振

无源电路的带通频率响应由多个谐振组合而成，因此 FDM 方法是提升其仿真效率的最佳选择。此方法通常包含两个步骤。特征频率分析是模拟任意形状器件共振频率的关键。从特征频率分析中获得所有必要信息后，就可以在频域模态研究中重复使用。当需要更精细的频率分辨率来更准确地描述频率响应时，这样做能够提升仿真效率，如AWE方法所示。

为了无缝执行 FDM 分析，有几个方面需要注意。一方面，需要过滤掉 特征频率 解中可能存在的所有不需要的非物理低频结果。另一方面，需要考虑目标频率范围内所有可能影响器件性能的物理模式，以获得正确的结果。要满足这两个要求，需要对 特征频率 研究设置进行一些调整（如下方屏幕截图所示）。首先，建议选择 更大的实部 作为 围绕偏移量的搜索方法 的设置。其次，对于 搜索特征频率 设置，最低通带频率可作为一个参考值。最后，必须调整 所需特征频率数 设置（例如根据初步测试），以包含必要的模式数量。

为模型添加包含两个步骤的 频域模态 研究，图中突出显示了 特征频率 设置。

让我们来看一个 耦合线带通滤波器教程模型，尝试使用 FDM 方法进行仿真分析。先以 50 MHz 的频率步长对 3.00 GHz 和 4.20 GHz 之间的仿真频率进行扫描，运行一个常规的 频域研究 。

耦合线带通滤波器教程模型（左）及以 50 MHz 频率分辨率进行离散频率扫描的仿真结果（右）。整个目标通带内的 S 参数图看起来并不平滑。

接下来，运行 频域模态 研究，并按照上文所述设置每个研究步骤。使用分辨率提高了50 倍的频率步长运行研究，并检查结果是否有更优。与 AWE 方法一样，FDM 方法研究得到的 S 参数图看起来更平滑，包含的信息量更大。例如，它显示了最初缺失的所有 S11 参数波纹。如果您对此方法的验证感兴趣，可以运行相同分辨率的常规扫描，并检查结果是否一致。

请注意，特征频率分析包含一个集总端口，作为额外的载荷因子影响仿真，因此计算出的 S 参数的相位与常规频率模型计算的相位不同。计算结果仅和不包含相位的 S 参数值兼容，如以dB为单位的值、绝对值、反射率或透射率。

分别由 频域，模态（FDM）和离散 频域 仿真计算出的 S 参数图。使用 FDM 方法计算的结果精度提高了 50 倍。

这与本文的主题并无直接关系，但在最后一张图中，可以看到到特殊的图形标记，它可以突出显示 S11 参数图的所有局部极小值以及 S21 参数图的通带。COMSOL Multiphysics 最近对结果评估功能进行了另一项改进，即从图表中提取交互式结果，将结果的信息性和交互式价值提升到了一个新的水平。

使用精细频率分辨率时的数据管理

如前所述， AWE 或 FDM 方法对如何细化频率扫描并没有真正的限制。不过，如果分辨率真的很高，解中将包含大量数据，从而导致在保存模型文件时，文件大小将大幅增加。在大多数无源RF和微波器件设计中，我们通常只对 S 参数感兴趣，因此在这种情况下，没有必要存储所有的场解。在研究的 在输出中存储 部分选择适当的选项，就可以控制模型保存计算的解。例如，可以只添加包含 S 参数计算边界的一个或多个选择。指定这些边界为 端口 或 集总端口，与整个仿真域相比，这些选择通常很小，因此总文件大小可以大幅减小。

请注意，在设置端口时，可以在指定选区后单击 边界选择 部分中的 创建选择 图标添加这种显式选择。然后，可以在相关研究步骤的 在输出中存储 部分添加由端口创建的所需的显式选择。

选择了2个 集总 端口的频域，模态 研究步骤的 在输出中存储 部分。您可以在 图形 窗口中查看这些选择的位置。

案例库中的教程模型

这篇博客介绍了COMSOL 软件中的 2 个强大的仿真功能，可以帮助您更快、更高效地模拟无源 RF 和微波器件。下列为 COMSOL 案例库中的一些相关教程模型，您可以浏览下载，进一步了解这些方法的使用：

• AWE 方法
  • 消失模圆柱腔滤波器
  • 电路量子电动力学 CPW 谐振器
  • 微带贴片天线
  • 采用SMA 连接的Wilkinson功分器
• FDM 方法
  • 级联矩形腔滤波器
  • 耦合线带通滤波器
  • 共面波导带通滤波器
  • 波导虹膜带通滤波器

文中演示的方法和研究是 通用的，不仅适用于RF仿真，在涉及如声学、力学、微机电系统(MEMS)和波动光学计算中，这些方法也尤其有用。

下一步

了解 COMSOL 中可用于RF和微波仿真的其他专用功能:

理论简述

当电路中有一条或多条导线回路时，就会涉及电感的概念，这些导线回路（或线圈）可以由一匝或多匝导线组成。假设其中一个线圈连接源，可将其称为初级线圈；如果其他线圈连接负载，则称为次级线圈。这些负载可以是其他电气设备的任意组合。

空间中的线圈、非线性磁性材料和磁体。一个线圈中的时变电流将在其他线圈中产生正比于拦截磁通量的磁场，其中偏置的非线性磁性材料将对这些拦截通量产生影响。

在线圈周围的空间中可能存在非线性磁性材料和磁体。非线性磁性材料会受到磁体、流经线圈的电流，或者在二者的共同影响下进入非线性状态。当向初级线圈施加时变电流时，包括初级线圈本身在内的所有线圈都会产生感应电动势（电压）。假设施加的信号频率远低于系统的谐振频率，就可以认为此电动势完全由时变磁场产生。基于这一假设，我们可以使用 线圈 特征进行计算。

当给定的时变电流流过第 个线圈时，其他第 个线圈的感应电动势与磁链¹的变化率成正比:

假定 是瞬时电流的唯一函数，应用链式法则：

可以看到，感应电压为关于电流的增量电感 和施加电流的变化率 的乘积。请注意，如果系统中的所有材料都是线性，不存在磁体，并且忽略导体中的电感损耗，那么上式可以简化为:

 
式中， 是视在电感，只要使用了 线圈 特征，软件就会默认计算。另一方面，计算增量电感还需要一些额外的步骤。

要理解如何计算增量电感，首先需要了解磁链。在工程类基础教材中，磁链通常被表述为：对激励线圈 在表征线圈 的导线环表面 所产生的磁通量 进行积分:

然而，如上图所示，大多数线圈的横截面积都很大，因此不可能简单地定义一个表面 。应用散度定理和 ，可以通过磁矢势 与表征线圈中电流方向的 点乘后的体积分来计算 ：

使用 线圈 特征时，软件会自动计算出这一数值，并将其称为线圈级联通量。

这个量可以是许多不同变量的函数，尽管我们之前假设它只是瞬时电流的函数。现在，让我们来看看如何求导数来提取增量电感。

计算增量电感

要计算增量电感，需要评估所有线圈中的线圈级联通量关于初级线圈施加电流的导数，这可以通过 灵敏度 接口实现。我们在使用 COMSOL Multiphysics^® 计算设计灵敏度的博客中介绍过这个接口，现在简要回顾一下。首先，要定义 全局目标 特征，其中需要输入线圈级联通量的表达式。还需要定义至少一个 全局控制变量 用于计算目标函数微分。然后，输入一个与流经初级线圈的直流电流相乘的变量名。通过这种设置，可以将 灵敏度 研究步骤与施加电流的 辅助扫描 相结合，计算施加电流范围内的增量电感。

在 灵敏度 接口中定义目标函数。

在 灵敏度 接口中定义控制变量。

使用 线圈 特征中的控制变量设置关于电流的微分。

在一定范围内扫描电流，同时计算灵敏度。

求解后，创建一个引用 计算组 的 插值 函数，以便在模型的其他地方使用增量电感的计算结果。

了解这些基本理论和工作流程后，现在让我们来看几个示例。

非线性电感器

首先，我们模拟了一个由合金铁氧体制成的磁芯，合金铁氧体是一种损耗极低的非线性磁性材料。磁芯从内部和外部包裹着一个线圈。我们采用了二维轴对称模型，其中线圈由 80 匝直径为 1 mm 的导线组成，工作频率为 50 Hz，因此这些导线的趋肤效应可以忽略不计，可以通过直流电阻准确预测线圈的交流电阻。在这个示例中，我们可以使用 多匝线圈域 特征在时域中求解，以获得在施加正弦电压作用下通过电感器的非正弦电流。

BH 非线性磁芯和环绕线圈组成的电感器。

首先，求解该模型在一定直流电流范围内的电感值，得到如下图所示的增量电感，以及用于对比的视在电感。

由非线性磁芯材料制成的电感器在一定直流电流范围内的增量电感和视在电感。

非线性电感器的等效电路模型，其中增量电感是电流的函数。

获得增量电感后，我们就可以在电路模型中使用它来快速预测瞬态行为。除了默认的 接地节点 特征外，建立电路模型只需要三个特征：

• 电阻 特征
• 电感器 特征
• 电压源 特征

使用一个 电阻 特征，阻值设置为使用 线圈 特征计算出的电阻值。在此基础上，添加一个 电感器特征，其非线性电感由存储了之前计算的增量电感的插值表定义。因为非线性特性与电流符号无关，所以可以将该非线性电感设为电流绝对值的函数。最后，将 电压源 特征串联接入。这三个特征共同创建了一个可预测响应的集总模型，将其计算结果与有限元模型的结果进行对比。请注意，在前几个周期内，结果表明仅仅只是开始接近此非线性系统的周期性稳态响应。

施加交流电压源时流经电感器的电流。电路模型和磁场模型的计算结果一致。

我们还可以通过傅里叶变换将这些时域数据转换到频域，以更清晰地识别由材料非线性引入的高次谐波。由于电路模型可以快速求解，我们还可以快速检查各种工作条件。不出所料，当设备进入非线性区时，会出现更多的高频分量。

电流的频谱图及其随峰值电压的变化。

含偏置磁铁的非线性电感器

为了便于说明，我们现在将上述示例进行修改，在磁芯旁边放置一块磁铁，磁铁将对线圈级联通量做出贡献，并使非线性材料发生偏置。现在，增量电感取决于施加电流的大小和符号。值得注意的是，正弦电感包含了磁铁本身对并联磁通量的贡献，但这种不随时间变化的磁通量不会对反向感应电压产生影响。磁铁只会改变系统内任一非线性材料的 B-H 关系。也就是说，磁铁不会影响仅由线性材料制成的电感器的响应。不过，必须牢记的是，磁铁始终会在正弦电感中引入偏置。因此，只要模型中存在磁铁，即使所有材料都是线性的，最好也使用增量电感。

放置在 B-H 非线性磁芯顶部的磁铁会使响应偏置。

在偏置电感器中，增量电感与直流电流的符号不对称。

增量电感可再一次用于电路模型，我们再次看到，除启动期间外，二者的计算结果非常吻合。启动期间的这种不一致，凸显了用于计算空间变化场及磁芯饱和空间演变的模型与集总模型之间的差异。

空间有限元模型与包含偏置增量电感的集总电路模型的计算结果基本一致。

变压器的非线性响应

接下来，让我们来看一个由围绕合金铁氧体磁芯上的两个相同线圈组成的变压器示例。由于 和 ，对称性不仅可以用来减小模型大小，还可以减少计算量。一般情况下，增量电感可以是 （初级电流）和 （次级电流）的函数，但对于这种对称结构， ，我们只需要计算增量电感 和 ；保持 的情况下，在 的范围内计算，无需对两个变量进行扫描。

由围绕在对称磁芯上的两个相同线圈组成的变压器，图中可以看到两个对称平面。

计算出这两个增量电感后，就可以使用一组函数来定义互感矩阵的所有四个项。这些项可以在同一变压器的电路模型中使用。由于存在非线性，两个线圈之间的耦合通过 电流控制的电压源 特征模拟，如下图所示。

含非线性磁芯的变压器等效电路。

使用完整的三维模型求解该变压器的响应需要大量的计算成本，而使用电路模型求解则非常快速。尽管在所有可能的运行工况下计算增量电感矩阵非常重要，但我们最终得到的结果还是非常吻合。为了提高计算效率，可以通过 批处理 或集群扫描 的并行方式一次性计算所有工况，以充分利用所有可用的计算资源。

施加在初级线圈上的正弦交流电压会在初级线圈和次级线圈上产生非线性电流。使用完整的三维模型和电路模型求解的初级线圈上的电压和次级线圈上的电流的对比。

螺线管线圈的动态响应

现在，让我们来看一个由铁质外壳内的线圈和铁质柱塞组成的螺线管。柱塞的安装方式使其只能沿其轴线移动。假设铁的磁导率在预期磁场范围内保持不变，并忽略材料的非线性。同时假设外壳和柱塞是绝缘材料，能将绕轴线的所有感应电流降至最低，因此可以将铁芯视为无损耗材料。

由铁制外壳内的线圈和由弹簧固定的铁柱塞组成的螺线管线圈。

弹簧将柱塞固定在壳外的位置以保持平衡。当向线圈施加电压时，电流开始流动，并推动柱塞向中心移动。在这种情况下，不存在材料非线性，因此级联通量与瞬态电流 呈线性关系，但与柱塞的 z 向位置 呈非线性变化：

因此，根据链式法则，反向感应电压为：

式中第一项考虑到了视在电感随柱塞位置变化这一事实。当柱塞在非零磁场中以速度 运动时，第二项引入了一个额外的反向感应电压。

考虑到级联通量与施加的直流电流（ ）呈线性关系，第一个方程对位置进行微分得到：

因此，为了计算关于位置的导数，结合使用 灵敏度 接口与 动网格 接口，在保持直流电流不变的情况下，计算级联通量关于 z 位置无限小变化 的偏导数：

我们通过 动网格 接口引入了 z 向位置的有限和无限小变化，然后对无限小位移（）求偏导，并沿柱塞行程的一系列不同位置（）进行扫描。通过偏导结果，现在可以建立一个简单的机电集总模型，将电路模型与柱塞运动方程结合起来。

机电集总模型由一个电路模型和一个集总机械模型组成，其中集总机械模型由柱塞运动时的力、与位置相关的视在电感和反向感应电压耦合。

由集总系统的示意图可以看到，电气系统通过力与机械系统耦合。要理解力的表达式是如何得出的，让我们先来看看系统中随电流和柱塞位置变化的总磁能的表达式：

柱塞上的总力可以通过虚功方法求得，对于线性磁性材料，轴向力可以通过总磁能关于无限小位移的偏导数求得：

也就是说，力是通过线圈的电流和电感关于位置的偏导数的函数，这一点我们已经计算过了。因此，在模拟螺线管的同时，我们还要求解柱塞位置的常微分方程：

式中， 是柱塞的平衡位置。这个方程可以通过 全局常微分方程和微分代数方程 接口或可添加到任何物理场接口的 全局方程 特征来求解。因此，该方程可以与 磁场 接口耦合来求解运动，还可以与 电路 接口耦合进行求解。

我们将使柱塞沿轴线自由振荡，并根据一组输入的结果来研究其产生的一些动态过程，目的是说明集总模型与用于计算集总参数的空间模型的计算结果非常吻合。

螺线管磁场的精确模型与集总模型的计算结果对比。

尝试建立集总模型

这篇文章，我们通过 4 个示例重点展示了 COMSOL Multiphysics^® 软件不仅可以提取增量电感，还可以计算线圈级联通量关于其他输入变量的导数。由此得到的量可用于构建简化的集总模型，从而准确预测系统的性能。

想尝试自己动手计算增量电感并建立这类集总模型吗？请点击按钮，进入 COMSOL 案例库，下载文中的示例模型：

参考文献

1. 1. D. Cheng, “Field and Wave Electromagnetics”, 2nd ed., Addison-Wesley, 1991

释放托卡马克的能量：微型核聚变技术

托卡马克装置通过增大体积和/或利用更高的磁场来实现更高的聚变增益，即它产生的核聚变能量与其运行所需的能量之比。然而，长期以来超导磁体技术限制了托卡马克利用更高的磁场的能力，因此研发人员不得不建造出如国际热核实验反应堆（ITER）这样的巨型装置，来实现更高的聚变增益。CFS 与 MIT 共同探索了一种由铜磁体和更高的磁场组成的 Alcator 托卡马克。然而，这些托卡马克只是将尺寸问题换成了铜的限制，因为铜是一种阻性材料，其运行所消耗的能量比之前的设计要高得多。因此，“这种方案并不是经济可行的核聚变能源”，CFS 联合创始人兼核聚变技术研究员 Dan Brunner 在 COMSOL 核聚变主题日的主题演讲中解释说。

之后，CFS 联合 MIT 设计了一个高场托卡马克，该装置可以利用更高的磁场，而且不会受到之前设计存在的尺寸问题或材料限制，这要归功于高温超导材料的使用。为了实现这个目标，他们建造并使用了一个性能完整、近乎全尺寸的高温超导磁体。目前，CFS 正致力于研究 SPARC 项目，这是一个概念验证性的托卡马克装置，目标是实现净聚变增益。除此之外，CFS 还计划在 2030 年代初建造一座旨在将核聚变能纳入电网的发电厂（ARC）。在实现这一目标之前，CFS 将继续借助仿真加深对 SPARC 的理解。

Brunner 说：“现在，我们可以设想一条不同的道路，不必像从前那样不得不从大变到更大，而是仅稍微变大并能利用更高的磁场来建造一个可行的核聚变反应堆。”

图 1 CFS 的 ARC 核聚变装置的预期时间轴。图片由 CFS 提供。

借助仿真应对核聚变挑战

虽然托卡马克仿真是一项众所周知的挑战性项目，但 CFS 仍成功使用 COMSOL Multiphysics^® 软件实现了对其设计的系统化拆解、内部作用力模拟，以及对复杂物理现象的深入观察。

计算冷却液和冷却系统

超导体需要维持在超低温状态下才能正常工作，并避免发生如淬火等热失控事件。然而这些超导体必须在 SPARC 内部核聚变产生的几乎难以想象的高强度能量源附近工作，因此面临挑战。CFS 希望借助仿真技术来模拟和测试可能的解决方案。Brunner 介绍说：“因为有许多不同的能量源可以进入超导体，所以冷却至关重要。需要让制冷剂在超导体中流动，以使其保持在工作温度范围内。”

图 2 SPARC 内部的电缆装载着流动的制冷剂，以保持超导体的温度。图片由 CFS 提供。

Brunner 及其团队模拟了三种最常见的制冷剂（氢、氦和氖）在 SPARC 中的温度范围，并观察了传热模拟的输出结果。从这些数据中，Brunner 团队能够探索他们可能使用的不同类型的冷却系统的优缺点，而无需让任何超导体或其他材料承受不必要的风险。

图 3 聚变产生的热量会将大量能量注入电缆中，并有可能使超导体失效。这就凸显了测试不同制冷剂的必要性。图片由 CFS 提供。

在合适的条件下测量材料强度

除了冷却之外，仿真在提供 SPARC 中材料所受力的信息方面也发挥了重要作用。通常，高场托卡马克会使其结构经受极端工况，对于高温超导设计来说尤其如此，因为它的磁场极强。结构承受的应力与磁场的平方成正比，因此整个装置材料承受巨大的应变。超导体及其固有的低应变极限进一步凸显了通过仿真测量预期受力的必要性。

电流与磁场在线圈上相交产生的力是结构必须能够承受的。CFS 发现，他们的多物理场模型能够计算不同合金在低温（约 20 K）条件下的强度和刚度极限，从而为 SPARC 的未来设计提供依据。通过模拟这些装置将要承受的力，CFS 可以确定其设计必须能够承受的明确应力和应变极限。

管理真空容器中的作用力

CFS 还使用仿真来优化 SPARC 的几何设计，以降低其真空容器中的峰值应力和温度。一般来说，真空腔的设计由巨大的瞬态力决定，而这正是仿真发挥作用的地方。真空腔面向等离子体的一侧必须经过工程设计，以从托卡马克内部的聚变等离子体中吸收极大（约 10 MW/m² ）的热通量。

图 4 CFS 即将建造的概念验证性托卡马克 SPARC。

环电流在等离子体内部流过用于保持其稳定性，在某些情况下，电流控制可能会失效，进而引发中断故障。这些故障会产生巨大的力，因此需要在总体设计中加以考虑。CFS进行了瞬态电场和磁场模拟，以确保其所采用的材料能够应对这些干扰。

在这部分演讲中，Brunner 讨论了麻省理工学院在进行高级偏滤器实验（ADX）期间开展的多项仿真研究。ADX 实验采用的真空腔设计是 CFS 公司目前托卡马克设计的前身，其中 COMSOL Multiphysics^® 被用于研究真空腔设计中的瞬态磁场以及由此产生的力、应力和位移。(点击此处了解更多相关信息）。

图 5 上图为 ADX 结构模型的几何结构，紫色边界为结构的固定位置。应力和位移的仿真结果说明需要对设计进行加固。当在 ADX 设计中增加支撑块后，下方的模型几何结构显示了对应的新增固定边界。

仿真助力推动核聚变商业能源发展

技术进步带来了新的挑战。CFS 认为超导磁体是实现未来磁核聚变的关键，但在探索其应用前景的过程中也发现了诸多需要优化的设计环节。虽然使用 COMSOL Multiphysics 软件能够精确模拟每一个案例，但对计算要求很高，这也正是创造力和软件开发起作用的地方。

CFS 的 IT 团队建立了多个 Amazon Web Services (AWS) HPC6as 来分配解决方案。这使得该团队能够在纵向和横向扩展其计算能力，从而能够同时执行更多的任务，并且每个任务可以在 50,000 多个内核上使用更多的 CPU。由于CFS 持有 COMSOL 浮动网络许可证，因此对复杂的聚变进行仿真变得不那么困难。“它使我们的仿真时间和成本降低了至少 50%，从而加快了运行速度。它还使我们能够在至关重要的时间尺度上对正在进行的工作做出决策。” Brunner 总结说。

下一步

观看 CFS 公司的主题演讲视频，了解更多关于核聚变的挑战性过程，以及其在该领域的研究进展。

超材料简介

超材料是由亚波长组件组成的人工构造结构。这些结构展现出各向异性色散特性，可以通过改变组成单元的形状、几何结构、尺寸、方向和材料特性来控制其电学特性，如介电常数、磁导率和电导率。通过合理选择控制参数，可以将超材料设计为具有金属（负实介电常数）或电介质（正实介电常数）特性。金属或等离激元超材料展现出两种不同的拓扑：双曲型和椭圆型。在双曲拓扑中，正交轴上的介电常数符号相反；在椭圆拓扑中，所有方向上的介电常数均为负。

这种等离激元超材料具有亚波长周期性和尺寸，可以通过周期性排列的金属–电介质层以及嵌入电介质中的金属纳米棒来构建。双曲波在超材料结构内部的传播被高度限制，其波长比自由空间中的波长小 100 倍。这种独特的电磁特性使得双曲超材料在如增强超透镜效应、亚衍射成像、传感、负折射、能量收集，以及量子和热工程等潜在应用中与传统各向同性材料截然不同。

接下来，我们将讨论采用半经典电磁方法计算层状金属-电介质超材料的介电常数张量分量。

计算超材料介电常数：仿真vs.有效介质理论

假设一个线性（垂直）极化电点偶极子源位于双曲超材料附近的空气中，该双曲超材料由周期性定向的亚波长金属–电介质层组成。偶极子辐射的消逝场与超材料结构耦合，激发出两种类型的波：沿金属–空气界面传播的表面等离激元和在超材料内部传播的双曲波。

位于超材料结构附近空气中的电点偶极子示意图。该结构由周期性排列的金属层和具有亚波长厚度与周期性的电介质组成。

超材料的各向异性相对介电张量 可以通过本构关系计算，用电位移场 和电场 表示为

1

假设超材料没有磁性， 的径向和垂直分量可表示为

2

3

在 和 已知的情况下，方程 2 和 3 可用于计算超材料的介电常数张量。为了在 COMSOL Multiphysics^® 软件中计算这些值，需要使用 up 和 down 算子计算平均电位移场和电场分量。然后，使用 平均 算子对本构关系 进行积分，计算有效介电常数。需要强调的是，这些算子是在超材料的金属–电介质内部边界上执行的，用于估算边界两侧不连续的场。

计算超材料介电常数的另一种方法是有效介质理论。在亚波长范围内，对角线分量可通过下列有效介质理论¹ 计算

4

5

式中， 是金属的填充率。 和 分别为金属层和电介质层的厚度； 和 分别为金属和电介质的相对介电常数。

方程 4 和 5 表明，超材料的各向异性色散取决于金属–电介质层的厚度和填充率。 和 的值可正可负，取决于层厚度和材料特性。

为了进一步说明，假设一种由银（金属）和二氧化硅（电介质）组成的超材料，相对介电常数张量对角分量的实部与金属填充率 的关系如下图所示，图中显示了电介质、双曲型和椭圆型三种状态。下图中， 表现出共振行为，因为它取决于相邻金属层之间的电磁耦合； 则显示出平滑的变化。在双曲状态下，介电常数张量的分量符号相反。在 较大的情况下， 的值受金属体积增大的影响，且为负值，产生椭圆拓扑。当 非常小时，金属对超材料特性的影响可以忽略不计，超材料表现为各向异性电介质。

超材料有效相对介电常数对角线分量的实部与金属填充率的函数关系。超材料由具有亚波长厚度和周期性的银层和二氧化硅层组成。

接下来，我们将详细介绍在超材料中激励双曲波的仿真设置。

双曲波激励仿真

本节探讨了 COMSOL Multiphysics^® 软件中利用附近电点偶极子辐射的场模拟超材料中双曲波的传播的能力。模拟的超材料由周期性排列的银和二氧化硅薄层组成，材料属性取自软件的内置材料库。使用 COMSOL 附加产品波动光学模块中的 电磁波，频域 接口和二维轴对称几何进行模拟。如下图所示，弱贡献 节点用于定义电点偶极子，完美匹配层用于吸收电波并尽量减少不必要的反射。运行一个波长域研究步骤来求解域场。运行另一个波长域研究步骤来计算超材料的有效介电常数张量与波长的关系。由有效介质理论（方程 4 和 5）和本构关系（方程 2 和 3）计算介电常数张量分量与自由空间波长的关系。

在源点使用弱贡献定义线性（垂直）极化电点偶极子辐射的电场。波长域研究步骤用于求解域场和超材料色散。

结果

运行模拟研究1后，可以直观地看到超材料中被激励的双曲波。下面的动画显示了光子能量为 2.6 eV 时的瞬时电场。如上所述，偶极子激励了在超材料内部传播的双曲波模式，以及在超材料-空气界面从源点向外径向传播的表面等离激元。

超材料中被激励的双曲波的瞬时电场和在超材料–空气界面传播的表面等离激元。

运行模拟研究 2 后，可以计算出超材料的有效相对介电常数。使用有效介质理论计算和使用方程 2 与方程 3 本构关系计算的结果非常吻合，如下图所示。

使用有效介质理论（实线）计算和通过仿真（标记点）模拟的超材料有效介电常数的对角线分量。

为了进一步直观地展示场分布如何随光子能量的变化而变化，下面的动画演示了光子能量从 2.6 eV 变化至 1.4 eV 时双曲波的电场模。模拟结果表明了双曲波的分支如何随光子能量的变化而演变。

超材料内部双曲波的变化与光子能量从 2.6 eV 变化至 1.6 eV 的函数关系。

本文所讨论内容也可用于模拟不同类型的等离激元材料，以及探索相关的光物质相互作用。

动手尝试

想尝试自己动手模拟双曲超材料吗？请单击按钮，下载文中讨论的模型。

参考文献

1. T. Li and J.B. Khurgin, “Hyperbolic metamaterials: beyond the effective medium theory”, Optica 3, pp.1388–1396, 2016

扩展阅读

• 了解有关超材料的更多信息，请阅读以下博客:
  • 使用 COMSOL Multiphysics^® 开发用于设计超透镜的仿真 App
  • 在高频电磁学中模拟石墨烯材料
  • 通过仿真分析特殊多孔超弹性材料

太赫兹波段简介

电磁波频谱的频率范围横跨大约 15 个数量级，几乎所有的电磁波段已被成功地应用到从远程通信到癌症治疗等各个领域。然而，由于太赫兹波的产生和检测存在技术困难，因此，频率范围大约在 0.1 THz 到 10 THz 之间，常被称作电磁频谱 “最后的前沿”太赫兹波段，一直未能实现大规模应用。直到最近，由于与太赫兹波产生和检测相关的技术创新在过去几十年里取得重大进展，太赫兹波段的商业应用似乎将要普及。事实上，6G 技术的运行频率可能就在太赫兹范围内。

图 1 太赫兹光谱位于微波和红外波谱范围内。

太赫兹波段的吸引力不仅仅在于通过更高的频率实现更大的带宽。许多材料，例如织物和纤维素等，对太赫兹辐射的吸收并不强烈，因此太赫兹成像技术能够“透视”衣物和包装材料的内部信息。另一方面，由于许多分子具有太赫兹能量的旋转和振动态，会强烈吸收太赫兹辐射，因此在正确的设置下，可以通过太赫兹图像获取准确的化学成分信息。此外，太赫兹波是非电离的，因此对人体安全无害。由于这些原因，太赫兹成像技术在安检类应用中成为 X 射线的理想替代品。

光导天线是许多太赫兹器件的基本组件，因此，本文将重点讨论光导天线模拟，即使用 COMSOL 附加产品半导体模块和RF模块建立一个光导天线模型，来预测太赫兹器件的发射光谱和指向性。尽管光导天线在太赫兹波的产生和检测中均有应用，但为了简化分析，我们将重点关注光导天线作为发射器的情况。本文采用的设置主要来自参考文献 1。

光导天线是如何工作的？

光导天线的工作原理相当简单。在由低导电性半导体（如低温砷化镓，LT-GaAs，由砷化镓在低温下结晶时产生，具有大量晶体缺陷）制成的基板上，在导电终端之间施加直流偏置电压，然后采用快速脉冲激光照射终端之间的间隙，就可以触发光电效应。当激光的光子能量大于半导体的带隙时，激光脉冲就会激发产生电子-空穴对，从而迅速提升材料的导电性。在终端之间流动的瞬态电流脉冲，即 光电流，将激发产生电磁辐射脉冲。如果激光脉冲持续时间处于飞秒量级，此脉冲的频谱通常会落在太赫兹波段。一旦激光脉冲结束，由于低温砷化镓材料内部高度缺陷，载流子会迅速重组，导致电流密度呈指数级衰减。光导天线的示意图如下图所示。

图 2 发射模式下的光导天线。

使用 COMSOL^® 模拟光导天线

在这个模拟应用中，我们使用半导体模块中的 半导体 接口计算激光脉冲产生的瞬态电流密度，并通过RF模块中的 电磁波，瞬态 接口模拟太赫兹脉冲的产生。模型的设置如图 3 所示。为了最大程度的提高计算效率，我们使用了两个二维组件。在组件 1 中，首先求解 xz 平面上的电流密度，使电流主要在z 方向上流动。(该组件的坐标默认仍为 x 和 y，电流将沿 y 方向流动。）如下所述，组件 1 将被映射到组件 2）。然后，在组件2中模拟太赫兹波在 xy 平面上的传播，以使源电流密度能垂直施加在模型平面。

图3 光电导天线模型使用的几何结构。通过 半导体 接口（图中为 semi）求解 xz 平面（绿色）上的光电流，通过 电磁波，瞬态  接口（图中为 temw ）在 xy 平面（红色）上模拟瞬态太赫兹脉冲。沿 xz 平面和 xy 平面的交叉线施加光电流密度，作为边界源电流密度。

半导体接口设置

首先，我们来详细了解如何利用组件 1 中的 半导体 接口模拟光导天线的载流子动力学。采用二维方法是指，我们假定激光脉冲在砷化镓衬底内衰减极快，因此无需解析 y 方向上的光电流，而且可以从模拟域中移除被终端覆盖的衬底部分。为便于缩放，将面外厚度设定为 1 µm。除了如图 3 中所示的设置两个金属触点外，还需要添加一个 光跃迁 节点，来模拟激光脉冲产生的电子-空穴对。我们选择了一个简单的高斯分布在空间和时间上描述电场振幅。光束半径设定为 5 µm，以匹配间隙大小；时间脉冲宽度（高斯函数的标准偏差）设定为 100 fs，并具有 0.5 ps 的延迟。最后，需要考虑低温砷化镓中大量晶体缺陷（即陷阱）集中所导致的快速重组过程。这可以通过添加 陷阱辅助复合 节点，指定载流子寿命来实现。材料属性来自参考文献 1。运行瞬态仿真 5 ps，以充分模拟重组过程的复合。

将半导体模拟获得的主要结果作为终端之间的瞬态光电流密度。为了将其作为边界源电流密度施加在沿组件 2 中的两个几何图形的交线位置，需要设置一个 线性拉伸算子。指定各自几何图形中恰当的终点和起点后，可以使用 _comp1.linext1()_ 算子将组件 1 中的任意变量映射到组件 2 中。

电磁波，瞬态接口设置

获得光电流之后，就可以使用组件 2 中的 电磁波，瞬态 接口模拟太赫兹脉冲。该组件的几何结构仅包括一个衬底的横截面切面（假设衬底的总厚度为 5 µm），周围是一个圆形空气域。由于源电流将沿平面外方向流动，为提高计算效率，可以只求解电场的面外分量。为了抑制非物理反射，我们在外部边界应用了 散射边界条件 特征。要获得远场频谱，需要添加一个 远场域 节点（需要同时运行 时域到频域FFT 研究步骤），并在模型外部边界进行远场计算，该节点仅应用于空气域。最后，使用 表面电流密度 节点，将组件1 映射的光电流用作电流源。为了确保在频域中获得足够的分辨率，在 10 ps 条件下运行这项研究，而不是半导体接口中使用的 5 ps 条件。

在研究设置中，首先需要运行瞬态研究来模拟太赫兹脉冲的传播。为了计算远场频谱，必须通过 时域到频域 FFT 研究步骤将时域数据转换为频域数据。

结果

先来看半导体计算的结果。图 4 的动画显示了在模拟的第一个 2.5 ps 内，由于激光脉冲、电场和电流密度产生的电子-空穴对产生率密度。此外，图 5 还显示了终端电流和总产生率的一维曲线图。可以看出，由于脉冲持续时间远小于载流子寿命，因此光电流的衰减速度比产生率更慢。

图 4 从左到右依次为：半导体模拟的第一个 2.5 ps 内的产生率、电场和电流密度。

图 5  终端电流和总产生率与时间的相关性。在 0.5 ps 时达到激光脉冲的峰值功率。

现在，我们来看看太赫兹脉冲。图 6 中的动画显示了脉冲是如何从光导天线传播的。源电流密度通过线图显式在衬底表面（下边界）。图 7 绘制了两个不同点的脉冲波形。从这些图中可以看到，衬底的反射如何在初始波前之后产生额外的波纹。

图 6 衬底下边界上的源电流密度及其产生的出射太赫兹脉冲。圆的半径为 250 µm。

图 7 距离光导天线 100 µm 和 250 µm 处的电场（Ez）。

最后，结合 远场计算 节点与 时域到频域 FFT 研究，绘制出光导天线的远场频谱图。我们发现，在大约 0.75 THz 处，脉冲达到最强峰值，且一直到接近 5 THz 处都有明显的功率。此外，在比较正向（y 方向）和侧向（x 方向）的远场光谱时，我们看到由于衬底的原因，有轻微的指向性。

图 8 运行 时域到频域 FFT 研究获得的太赫兹脉冲远场频谱。在比较 y 方向和 x 方向的频谱时，发现由于衬底的存在而产生轻微的指向性。

我们应该注意到，这种简单的光导天线模拟方法有一定的局限性：

• 我们假设 GaAs 衬底内的激光强度衰减得足够快，可以进行二维处理，因此无法求解 z 方向上的光电流密度。
• 我们只模拟了终端之间平面上的太赫兹脉冲，因此忽略了金属终端对脉冲频谱和指向性的影响。这也意味着没有根据计算出的太赫兹带宽对天线形状进行优化。
• 我们模拟了只包括一个薄衬底的简单模型，不足以提供强大的指向性。更接近真实应用的模型应该包括更厚的衬底域和/或硅超半球透镜，来引导太赫兹光束。

在太赫兹脉冲模拟中，可以考虑建立天线几何结构的全三维模型来克服这些局限性。

结语

在这篇博客中，我们通过建立一个具有实际预测能力的简单模型，探讨了如何利用半导体模块和 RF 模块，基于第一性原理模拟太赫兹设备。文中介绍的模型模拟了光导天线太赫兹发射的频谱和指向性。您可以点击下面的按钮下载光导天线模型，尝试自己动手模拟！

参考文献

1. J. Zhang et al., “Numerical analysis of terahertz generation characteristics of photoconductive antenna,” 2014 IEEE Antennas and Propagation Society International Symposium (APSURSI), pp. 1746–1747, 2014; https://ieeexplore.ieee.org/document/6905199.

扩展学习

• 了解有关太赫兹模拟的更多信息，请查看太赫兹超材料仿真网络研讨会相关视频:
  • 用 COMSOL Multiphysics^® 模拟太赫兹超材料

表面贴装器件

表面贴装器件是一种贴装在印刷电路板或基板表面的无引线或短引线元件。贴装元件的方法称为表面贴装技术（SMT），通过焊接或浸焊工艺固定器件。该技术需要将表面贴装器件置于高温下，这会导致器件变形，从而阻碍其贴装到印刷电路板。为了模拟高温环境对器件的影响，在进行可靠性测试之前需要进行预处理。通过有限元仿真，工程师可以更深入地理解预处理过程对表面贴装器件的影响。

焊接表面贴装器件。获 Creative Commons Attribution-Share Alike 3.0 Unported, 2.5 Generic, 2.0 Generic and 1.0 Generic 许可, 通过 Wikimedia Commons共享。

预处理过程模拟

绝缘栅双极晶体管（IGBT）是表面贴装器件的一个典型示例。表面贴装器件可靠性测试的预处理模型模拟了一个绝缘栅双极晶体管模块，即贴装在一个功率半导体基板上的多个绝缘栅双极晶体管。该模型展示了如何利用建模和仿真分析表面贴装器件在电路板组装过程中经历的多次回流焊操作。在焊接过程中，表面贴装器件暴露在高温环境，这可能会造成内部损坏，尤其是当封装内有湿气的情况下。预处理的目的是在可靠性测试之前，以可控和可重复的方式产生电路板组装过程中产生的应力。此模型中使用的是表面贴装器件预处理序列的行业标准测试方法：JESD22-A113I 标准。

预处理过程有三个主要步骤:

1. 烘烤
2. 浸湿
3. 模拟回流焊的温度变化

如果模拟的器件显示出过大的应力和变形，表明需要重新设计回流焊工艺，例如减慢升温速度，或使用吸湿性较低的材料等其他电磁兼容性材料。

绝缘栅双极晶体管模块的几何模型。

烘烤

预处理过程的第一步是烘烤，该步骤通过高温去除结构中的水分。为确保温度分布均匀，逐渐加热绝缘栅双极晶体管，并在 125^°C 温度下烘烤 24 h。这一步骤可最大限度地降低回流焊阶段产生的热冲击。初始水分浓度为 10 mol/m³，塑封件外部边界的浓度设定为 0 mol/m³。如下图所示，该器件在烘烤过程中会变形为凹形。

左：烘烤步骤结束后的应力分布。右：烘烤步骤结束后，显示了结构变形的塑封件中的水分浓度。

烘烤步骤中的结构变形动画。

浸湿

预处理过程的第二步是测量回流过程中水分的影响，因为塑封材料（ EMC ）层内的水分可能会在回流过程中产生应力，从而导致可靠性问题。烘烤步骤后的浸湿是一种以可控的方式将水分引入塑封材料层的方法，这样可以确保在回流焊过程中可能产生的任何影响都是可重复的。在这个示例中，浸湿过程在 40^°C 下持续了 192h。烘烤后的结构是干燥的，因此初始浓度为 0 mol/m³。塑封件外部边界的浓度保持在 140 mol/m³，假设在该步骤中水分在外部边界达到饱和。最终绝缘栅双极晶体管发生的变形较其在烘烤步骤中的变形要小，变成了微凸形。

浸湿步骤中的结构变形动画。

回流焊

回流或焊接阶段用于将绝缘栅双极晶体管模块的温度提高到所用焊膏的熔点，以使其液化。 熔融焊料的回流是将绝缘栅双极晶体管模块连接到印刷电路板的关键。回流焊测试在浸湿步骤后直接进行，初始水分浓度取自上次浸湿过程的最终结果。在该模型中，回流过程在 21 min 内历经三个循环，期间最高温度达到 260^°C。在这一过程中，绝缘栅双极晶体管模块在温度峰值时呈凹变形，而在回流过程呈凸变形。这一步骤对器件造成的压力最大，而仿真模型有助于预测压力的位置和程度。

t= 6 min 达到回流步骤温度峰值时的应力分布（左），以及 t = 6 min 后达到回流步骤温度峰值时，显示了结构变形的塑封件中的水分浓度（右）。

回流步骤（3 个循环）中结构变形的动画。

进一步的测试

预处理过程中发生的变形仿真，可以帮助工程师更深入地理解变形对绝缘栅双极晶体管模块的影响，从而能够修改设计，避免损坏，同时提高产量和可靠性。还可以对该模型进行扩展，进一步测试到印刷电路板和表面贴装器件结构及其周围环境之间的热量传递，以及扩展为包括焊接材料的黏塑性等因素的更复杂模型。

更多测试

点击下方按钮，进入COMSOL 案例库，下载模型文档和 MPH 文件，学习如何建立预处理模型：

阅读下列博客，了解电子行业中半导体的更多信息:

• 基于密度-梯度理论的三种半导体器件模型
• Wolfspeed 使用 COMSOL Multiphysics 开发仿真 App 的原因
• 使用 COMSOL^® 计算和使用部分电感

无形的能量场

我们日常使用的大部分电力都来自高压到低压电力输电线，这些电力线会产生电场和磁场（EMF）。电力线可以传导强低频电流，产生随着距离的增加而迅速减弱的非电离电磁场。尽管如此，为了确保电力线对周围人和环境的影响保持在安全范围内，对其产生的电磁场的暴露和输出进行监控仍然非常重要。

图 1 远距离电力输电线模型。

接下来，我们将通过两个示例模型来探讨如何利用建模和仿真分析电力输电线产生的电场和磁场。这些示例将重点关注场强及其与电力线和铁塔的分布关系。

如何建立两种电力线模型

您可以在COMSOL 案例库中找到电力线的电场和电力线的磁场教程模型，模型中用两个塔架传输高压三相交流电。铁塔的相线上方装有两条屏蔽线，用于防止雷击造成损坏。在如此高电压的电力线路中，相线通常由几条较小的导线捆束而成。为了简化模型，每条相线只使用一根半径为 10 厘米的导线来模拟一束导线。在每个模型中，都将地平面设置为随机扰动面，以模拟地球的不规则性。

图 2 左图：电力输电线的照片，由 David Levêque 拍摄，图片来自 Unsplash 。右图：输电塔的几何形状。可以看到顶部的两条屏蔽线，以及由绝缘子固定的三条相线。

我们已经介绍了这两个模型的基本几何结构，接下来，让我们来看看它们各自的仿真结果。(请注意，如需获取建立这些模型的分步说明及其 MPH 文件，可以点击文末链接，至COMSOL 案例库中下载。)

电场模型

在电场模型中，用户可以设置每条相线的电压幅值和相位。(在图 3 所示的场景中，电压设置为 400 kV，相间隔为 120^º 。）此外，由于使用了边界元法，以及所有的边和表面均为固定电势，因此模型只需要在这些实体上建立网格。相比之下，采用有限元法时，模型需要在整个空气域内创建体网格，这将大大增加自由度的数量，并延长模型求解所需的时间。

仿真结果显示了线路在地表产生的电场模，以及空气中指示局部电场方向的流线。在电线附近，电场形成了一个分支图形。电场在靠近电线的地方最强，随着距离的增加而减弱。了解电场的传播距离可以帮助工程师确定建筑物与电力线的距离，从而最大限度地减少暴露，并确保电场强度符合相关规定。

图 3 电力输电线的电场模（表面图）和电场（流线图）。

磁场模型

在磁场模型中，每条相线都能传导 1000 A 的电流。与电场模型一样，磁场模型中的相也间隔 120^º 。模型中的所有外部边界都采用了默认的磁绝缘边界条件。

与电场模型一样，磁场模型的结果也显示了线路在地面上产生的磁场模和指示磁场方向的流线，这些流线形成闭合回路。该模型中的磁场也是在靠近电线的地方最强，随着距离的增加而减弱。

图 4 电力输电线的磁场模（表面图）和磁场（流线图）。

下一步

在这篇博客中，我们讨论了使用 COMSOL Multiphysics^® 建立的两个用于检查电力输电线产生的电场和磁场分布的案例模型。这些模型对于测量电磁场的范围和行为非常重要，可以帮助我们进一步了解电磁场如何与周围环境相互作用。

想尝试自己模拟电力输电线中的电磁场吗？您可以点击下方案例模型链接，获取文中讨论的模型及其详细分步说明:

• 电力线的电场模型
• 电力线的磁场模型

扩展阅读

阅读COMSOL 博客，了解更多有关仿真在电磁场暴露研究中的作用的信息:

• 通过仿真研究电力线附近的磁场暴露水平
• 使用仿真 App 分析电气设备的外部电场