COMSOL Multiphysics® 软件 6.4 版本扩展了传热模块的表面对表面辐射 功能,在使用射线发射 法时,除镜面反射外还加入了镜面折射。这对于解决涉及准直辐射源(如太阳辐射或激光光源)的辐射传热问题尤为有效。 本文,我们将深入探讨软件中的这些功能及其相关特性。
背景:折射光与折射仿真
首先,让我们来看一个你可能在博物馆里见过的装置:放置在桌面上的形状各异的透明玻璃片与曲面镜,平行光束与之相互作用。 玻璃的折射率高于空气,因此光线穿越这些部件边界时会遵循斯涅尔定律发生偏折,而反射与折射辐射的强度则由菲涅尔方程给出。当光线入射到镜面时,会发生镜面反射。光线折射穿过玻璃元件时,也会照亮桌面——尤其当光线聚焦时效果更为显著。
 桌面上放着两个光学元件:一个凸透镜和一个曲面反射镜。一个准直光源以小角度通过一侧的开口处照射桌面及光学元件。
桌面上放着两个光学元件:一个凸透镜和一个曲面反射镜。一个准直光源以小角度通过一侧的开口处照射桌面及光学元件。
假设我们需要计算入射光导致的桌面温度分布。从概念上讲,该建模问题包含两个部分:
- 计算入射辐照度
- 计算所有发射表面与吸收表面间的温升及辐射传递
我们进行如此划分是因为入射辐照度不受解的影响。即假设光源(遥远的太阳或激光光源)不会受到桌面温度的影响。
此外,这类问题通常具有以下特征:外部光源(太阳或激光)的辐射波长与受热部件发出的热辐射波长存在显著差异。即短波红外线或可见光照射结构时,会通过玻璃光学元件折射而不直接加热元件,而其他不透明物体发出的热辐射则主要为长波辐射。 由于玻璃在这些长波波长下通常呈不透明状态,因此会直接吸收这种长波热辐射而被加热。这意味着我们应采用所谓的多波段模型,即在多个(通常是两个)不同波段上计算热辐射。
我们可以使用射线发射 法来建立并求解此类问题。该方法结合了用于计算外部辐射源热负荷的正向射线发射 法,以及用于计算各表面所受周边表面辐射负荷的反向射线发射 法。该方法支持多波段辐射计算,可考虑镜面反射效应,并且从 COMSOL 6.4 版本开始,还可处理介质界面处的镜面折射现象。 为简化概念,我们将使用两个不同的表面对表面辐射 接口处理这两种波段:一个专门用于计算来自外部辐射源的辐射加热,另一个用于计算室温下物体之间的再辐射。
首先,我们观察下模型结果。然后再逐步说明模型的设置。如下图所示,桌面温度在两个点达到峰值:
- 入射光经透镜聚焦处
- 反射镜面聚焦光线处
尽管透镜和反射镜均直接承受光源照射,但二者均未出现显著升温。
在 COMSOL Multiphysics® 中建立模型
构建模型从几何结构开始,由多个对象构成:一个带有凸出侧边的木质桌面,其中一侧开有一个矩形孔洞。另构建两个玻璃对象:一个凸透镜,另一个是背面镀有反射层的曲面玻璃件。
 模型中使用了三个物理场接口: 固体传热 接口处理热传导, 外部辐射源产生的热通量则被作为热负荷进行建模。
模型中使用了三个物理场接口: 固体传热 接口处理热传导, 外部辐射源产生的热通量则被作为热负荷进行建模。
模型中包含了三个物理场接口:首先, 固体传热 接口用于在所有域内求解桌面与玻璃材料内的热传导;其次,所有暴露在空气中的边界均采用 表面对表面辐射 接口处理中长红外波段的辐射传热,并通过 表面对表面辐射传热多物理场接口的耦合功能与固体传热 接口相耦合。 需注意,玻璃虽然对人眼来说是透明的,但在较长波长下实际为很好的吸收体(因此也是很好的辐射体)。
最后,还有另一个表面对表面辐射接口。该接口被分配至所有固体部件的暴露边界,以及玻璃与桌面的界面。此接口专用于计算来自外部辐射源(太阳)的入射热通量,假设该辐射属于短波长范围。辐射源本身通过外部辐射源 特征进行定义,该功能指定了辐射通量和方向。 计算得到的沉积热量随后作为边界热通量添加至固体传热 接口中。
关于辐射模型的设置,木质桌面的大部分边界被定义为漫反射且高吸收性,发射率为 0.85。然而,面向入射太阳辐射的开口表面发射率为 0.05,这意味着它们对入射光具有漫反射特性。
 使用 不透明表面 特征对玻璃部件的表面进行建模,意味着这些表面既作为镜面反射体,也作为漫反射辐射体。
使用 不透明表面 特征对玻璃部件的表面进行建模,意味着这些表面既作为镜面反射体,也作为漫反射辐射体。
 不透明度 特征应用于计算外部辐照度的接口中,需与折射域表面的折射界面特征结合使用。
不透明度 特征应用于计算外部辐照度的接口中,需与折射域表面的折射界面特征结合使用。
在红外波段辐射接口中,玻璃边界被建模为不透明表面,其发射率为 0.9,漫反射率为 0,这意味着它们的镜面反射率为 0.1。这种建模方式很好地近似了玻璃在较长波长下的热行为。 另一方面,在计算太阳辐射的接口中,玻璃区域被建模为完全透明的,但其折射率由不透明度 特征定义。 自软件 6.4 版本起,新增了透明介质折射率设置用于定义域的折射率。几何模型之外的空域默认折射率为 1。在玻璃与空气交界处,应用折射界面 边界条件,通过菲涅尔方程计算反射与折射效应。
最后,曲面玻璃背面的镜面通过接口中的镜面反射 功能建模,用于求解入射光。该镜面在红外波段未建模,因其在该波段不可见。
在求解过程中,可采用自适应网格细化对加热区域生成更精细的网格。除温度场外,外部辐照度与外部热源的沉积热量等其他有用的可视化结果同样具有重要的参考价值。
结语
本文,我们展示了如何使用传热模块的功能实现对玻璃等折射材料的辐射进行建模仿真,这些材料在光学波长范围内被视为无损耗介质。但需要注意玻璃在较长波长下具有高损耗特性。 我们已经了解到,有一种解决方案是使用两个不同的表面对表面辐射 接口:一个用于短波长辐照,另一个用于环境温度下表面对表面的辐射传热。这两个接口均采用了射线发射 法。
同样值得一提的是,这项新功能与射线光学模块的功能存在差异:后者可追踪光源穿过光学系统的路径,并计算其在表面及域上的沉积热量。 传热模块的射线发射功能同样基于菲涅尔折射和反射定律,但采用所有偏振方向的平均处理方式;而射线光学模块则会额外计算并存储光线的偏振态。射线发射 功能经过了简化,仅适用于折射率恒定且无损耗的域。相较于射线追踪法,射线发射法具有显著的计算效率优势,因为它仅计算射线路径而不存储数据。在实际应用中,该方法既可以计算入射辐射,也能计算系统自身发射的辐射,这对于高保真热辐射仿真至关重要。
另一方面,射线光学模块的射线追踪法仅从指定的光源发射射线。它会计算并存储射线及其强度、偏振、功率和光程等参数。这些量对于基于光程的计算是必不可少的,例如干涉图、光斑图和像差。因此,射线光学模块适用于需要对光学系统性能进行模拟的用户。
两种方法可在单个模型中结合使用:先采用射线发射法计算辐射加热、随时间变化的温度分布以及由此产生的结构变形。再通过射线光学模块计算光学性能。此工作流程对于那些关注设备的结构-热-光学性能(STOP)建模的用户尤为实用,特别是针对设备在瞬态工作状态下的分析。
下一步
想深入了解 COMSOL Multiphysics® 在折射仿真方面的仿真功能? 请联系我们!
闭环地热换热系统利用电力和地埋管换热器从地下提取和释放能量,为建筑物供暖和制冷。使用地热供暖有助于减少碳排放,尤其是在电力来源为可再生能源的情况下。Renewable Energy 杂志上发表的一篇论文(参考文献 1)探讨了地源热泵系统中倾斜式地埋管换热器的优点。该论文的主要作者 Daniel Deacon 是一位地热交换专家和地热工程师,他向我们讲述了他是如何在这项研究工作中使用多物理场仿真的。
远离天然气
全球都在关注气候危机和减少化石燃料的使用,这促使能源行业开始寻求为建筑物供暖和制冷的替代方法,重点是减少天然气的使用并降低碳排放。使用非碳能源(如地源热泵)供暖是一种可行的替代方案,因为这些能源结合了电能和热能,而非纯粹的电能。地源热泵,或称为地埋管换热器(Borehole Heat Exchangers ),利用的是地下数百米处相对稳定的温度场。地热能源是一种比天然气丰富得多的资源。
地埋管换热器可作为大型地热系统中的关键驱动部件。它们是由高密度聚乙烯制成的大型管道,嵌入在灌浆柱中。它们采用一个闭环系统,流体在钻孔内的管道中循环,以便在地下和建筑物之间传递热量(图 1)。流体从地下几百米的土壤和岩石中提取热量。然后,这些能量被输送到热泵装置,热泵装置利用这些能量,将流体分配到整个建筑物的机械系统中。当建筑物冷却时,能量会被释放回地下。Deacon 将这一过程称为 “能量平衡”。将多个地埋管换热器组合在一起就形成了一个地埋管换热器场,这通常是为大型建筑物提供足够制热和制冷的能量时所必需的。
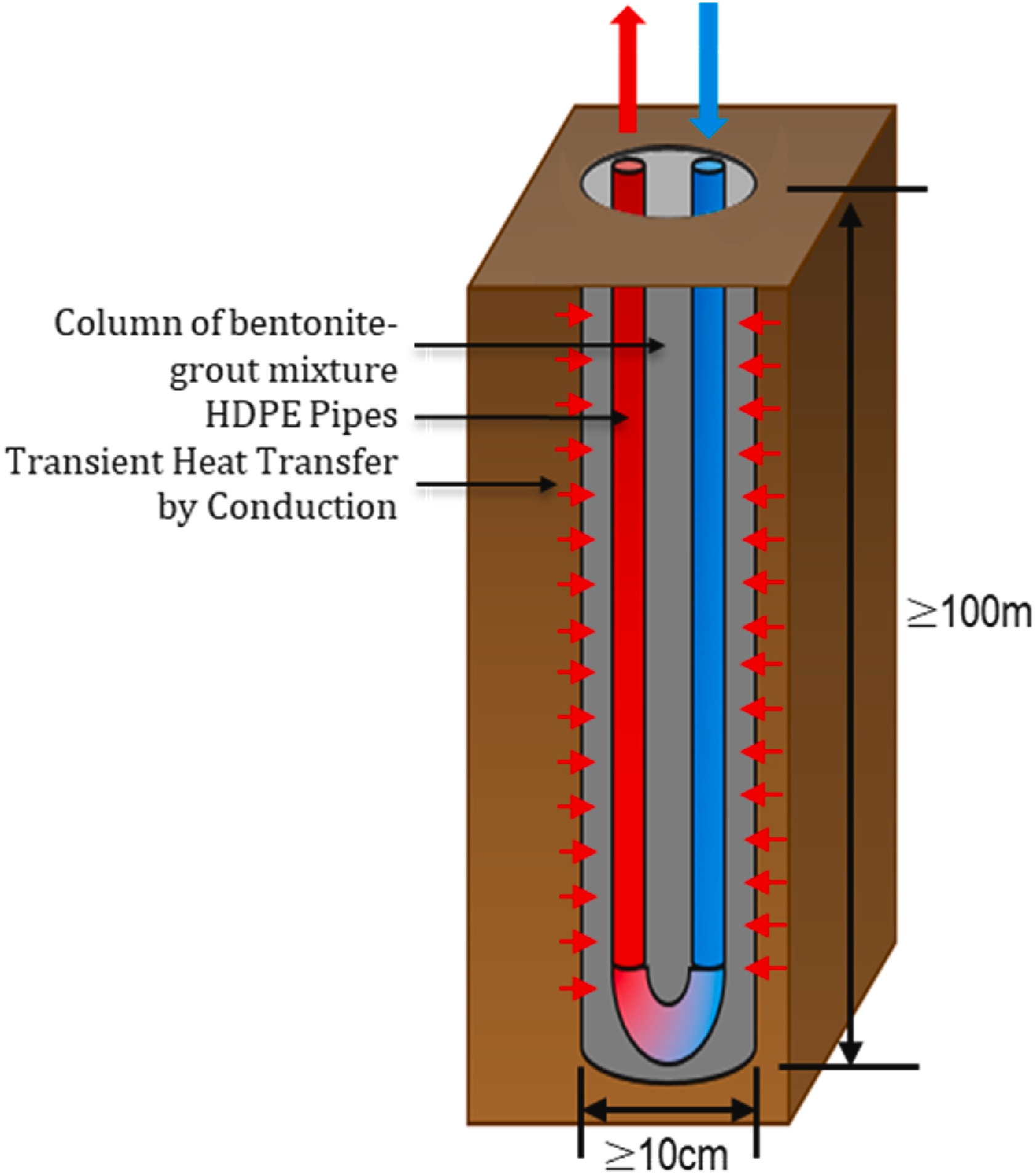
图 1. 一种垂直式地埋管换热器,它从地下提取热量,并将冷却后的流体送回地下。
在 Deacon 工作的加拿大多伦多,所有新建建筑都必须符合多伦多绿色标准 (参考文献 2),这是一项旨在减少碳排放的倡议。该标准对翻新改造也有要求。这些要求对工程师提出了挑战,因为他们必须找到一种方法来满足地面空间非常有限的现有建筑物的供暖和制冷需求。” Deacon 在论文中解释说:“通过倾斜式钻孔,相邻钻孔在地表处的间距最多可减少 90%。” 图 2 展示了这种钻孔间距的情况。
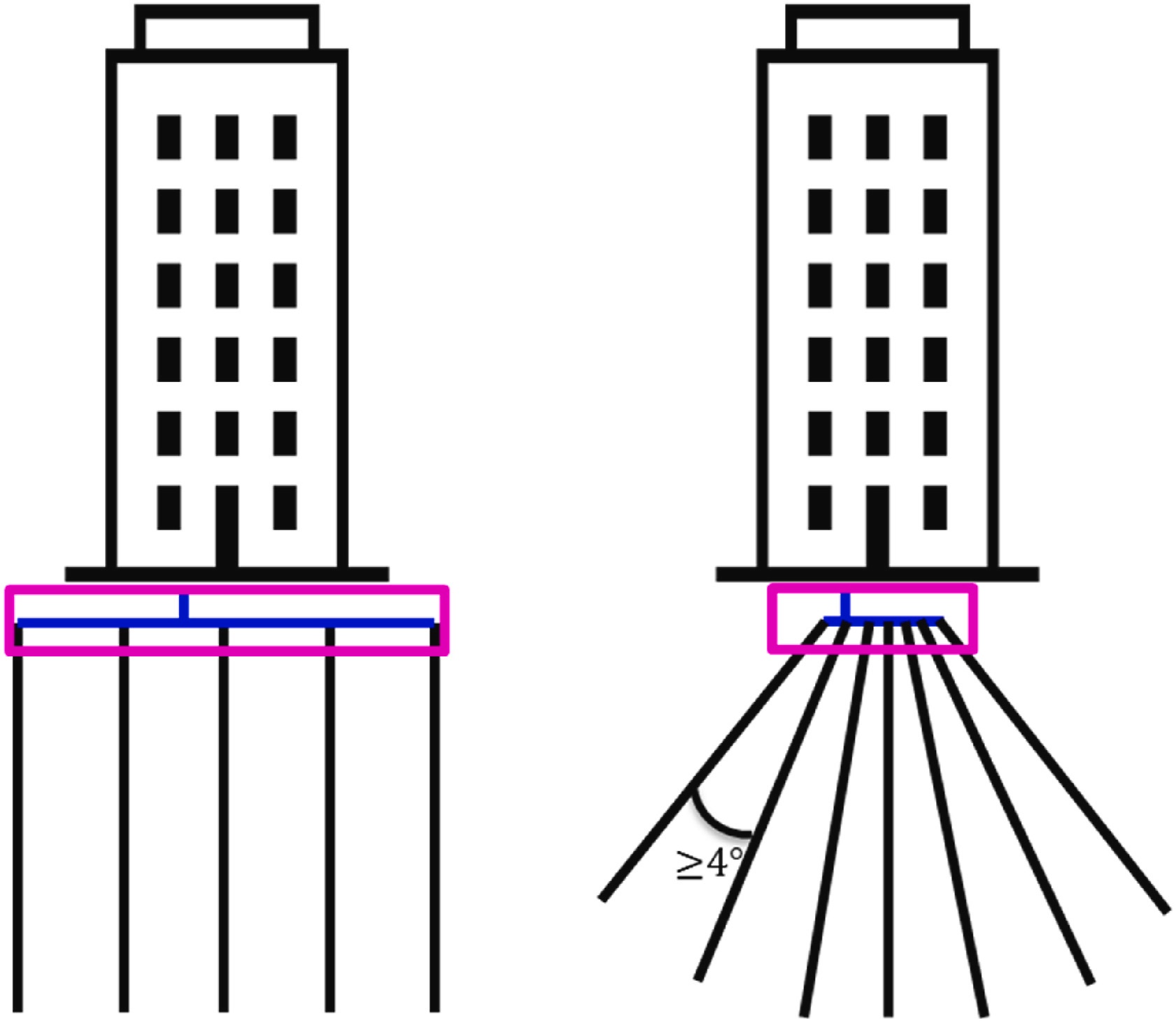
图 2. 倾斜钻孔可大大减少所需的地面面积。
由于大多数文献都是基于垂直式地埋管换热器的,因此行业内缺乏对倾斜式地埋管换热器的建模,这导致了对倾斜式地埋管换热器传热物理特性的假设。Deacon 使用 COMSOL Multiphysics® 仿真软件建立了倾斜式地埋管换热器的三维模型,并将其随时间变化的性能与垂直式地埋管换热器模型进行了比较。
协作与测试
Deacon 基于 Tolga Ozudogru 在 COMSOL Multiphysics® 中开发的地埋管换热器模型(参考文献 3)进行了扩展。该模型将地埋管换热器内的流体流动表示为一维管流,并与周围土壤和岩石等固体材料中的三维热传导相耦合。Ozudogru 将这种方法称为“伪管道法”,与建立完整的管道内流体流动三维模型相比,它节省了大量计算资源。伪管道法将 COMSOL Multiphysics® 中的 管道传热 接口与 固体传热 接口耦合起来。它将流经管道的流动和传热视为瞬态一维过程,并与三维固体域的边界耦合,三维瞬态热传导方程就是在这个边界上求解的。周围固体材料中热传导的三维数值模型采用了有限元法(FEM)。Deacon 使用 COMSOL 的附加产品——传热模块,开发了一个将计算流体动力学(CFD)和三维瞬态热传导相耦合的复合模型。该复合模型可以捕捉到倾斜式换热器中出现的多物理场效应。
这些模拟结果通过 Richard Beier 收集的实验数据(参考文献 4)进行了验证,该实验装置为一个矩形沙箱,其中心装有一个 U 型管换热器。流体在管道中循环,并在回路之间被加热。热敏电阻被放置在周围的沙子中,用于测量不同径向点的瞬态温度。然后,将入口(供水)的质量流量和温度作为数值模型的边界条件。结果表明,COMSOL Multiphysics® 对流体出口(回水)温度和一系列径向位置处沙子温度的预测值与实验结果非常吻合。
为了模拟 2 小时的断电情况,进行了一项中断试验。对流体施加热通量以模拟断电时的情况,而土壤域的初始条件和边界条件与团队进行的不间断试验中的相同,仅入口流体的温度和流速不同。COMSOL Multiphysics® 准确预测了断电 2 小时后重新启动循环泵和加热器后的温升,验证了实验数据中使用的瞬态热传导方程的解(图 3)。这些研究使 Deacon 确信,COMSOL® 能够准确模拟地埋管换热器的传热物理过程。
图 3. 左图:入口(供水)和出口(回水)处的流体温度的实验数据和 COMSOL 模拟结果之间具有高度一致性。右图:五个径向位置的温度实验测量值与 COMSOL 模拟预测值的对比。
倾斜式与垂直式地埋管换热器的性能对比
随后,这项研究分析了三种不同地埋管换热器的配置(图 4)在恒定注热速率下的热响应。本研究对以下几种情况的热性能进行了比较:
- 单个垂直式地埋管换热器(1V)
- 2 个平行的垂直式地埋管换热器,相距 5 米(2V)
- 1 个垂直式地埋管换热器和 1 个倾斜式地埋管换热器的配置,在地表相距 2.75 米,倾斜式地埋管换热器与垂直轴呈 3 度倾斜 (1A1V)
根据工业热响应测试中使用的典型功率,入口处的热功率为 20 KW。本研究模拟的总运行时间为 8760 小时,即 1 年。该研究的地层参数代表了安大略省南部的地面测量结果。在整个研究过程中,入口处的质量流量、热功率、流体的初始温度、比热容以及运行时间等运行条件都是恒定的,因此可以单独对热导率进行分析。
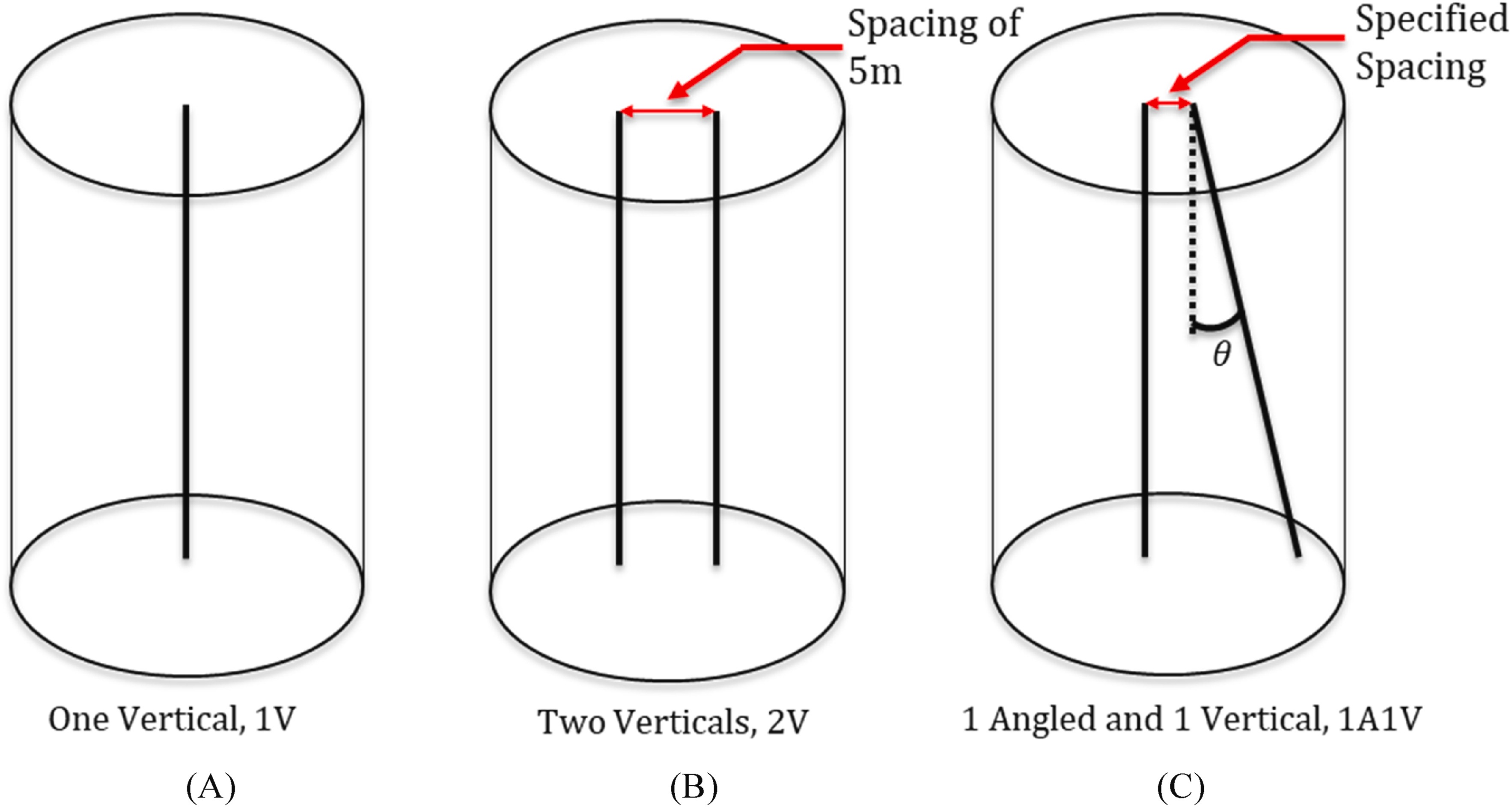
图 4. 用于分析热响应的三种地埋管换热器配置的可视化图。
1V 配置的传热效果被认为是最佳的,因此,通过将其他两种配置的流体温度与 1V 配置的流体温度进行比较,评估了这两种配置的性能。0 K 的温差代表最佳性能。由于地面空间有限,预计 1A1V 中的热相互作用比 2V 开始得更早。热相互作用表现为流体温差的增加(相对于 1V 配置)。不过,一旦 2V 开始产生热相互作用,预计随着时间的推移,1A1V 的效率会越来越高。
在 0–100 小时的运行时间内,两种配置的热性能都类似于 1V 配置,即达到了最佳标准(最大热传递)。在最初的 100 小时之后,1A1V 配置的流体温度比 1V 配置的流体温度高出 0.02°C。最大温差在约 690 小时时达到峰值,然后开始下降,直到 1053 小时,两者的温度曲线在此相交(图 5)。
当两条曲线相交时,2V 的温度曲线会迅速偏离 1A1V,这是因为在 2V 配置中,沿着换热器的整个深度存在热相互作用。1A1V 配置减弱了沿深度方向的热相互作用,导致末端的流体温差比 2V 低约 1.4°C。交汇点标志着 1A1V 的性能从轻微的不利影响向轻微的有利影响转变。该图表明,在更长的时间内,1A1V 配置比 2V 配置表现出更好的传热效果。
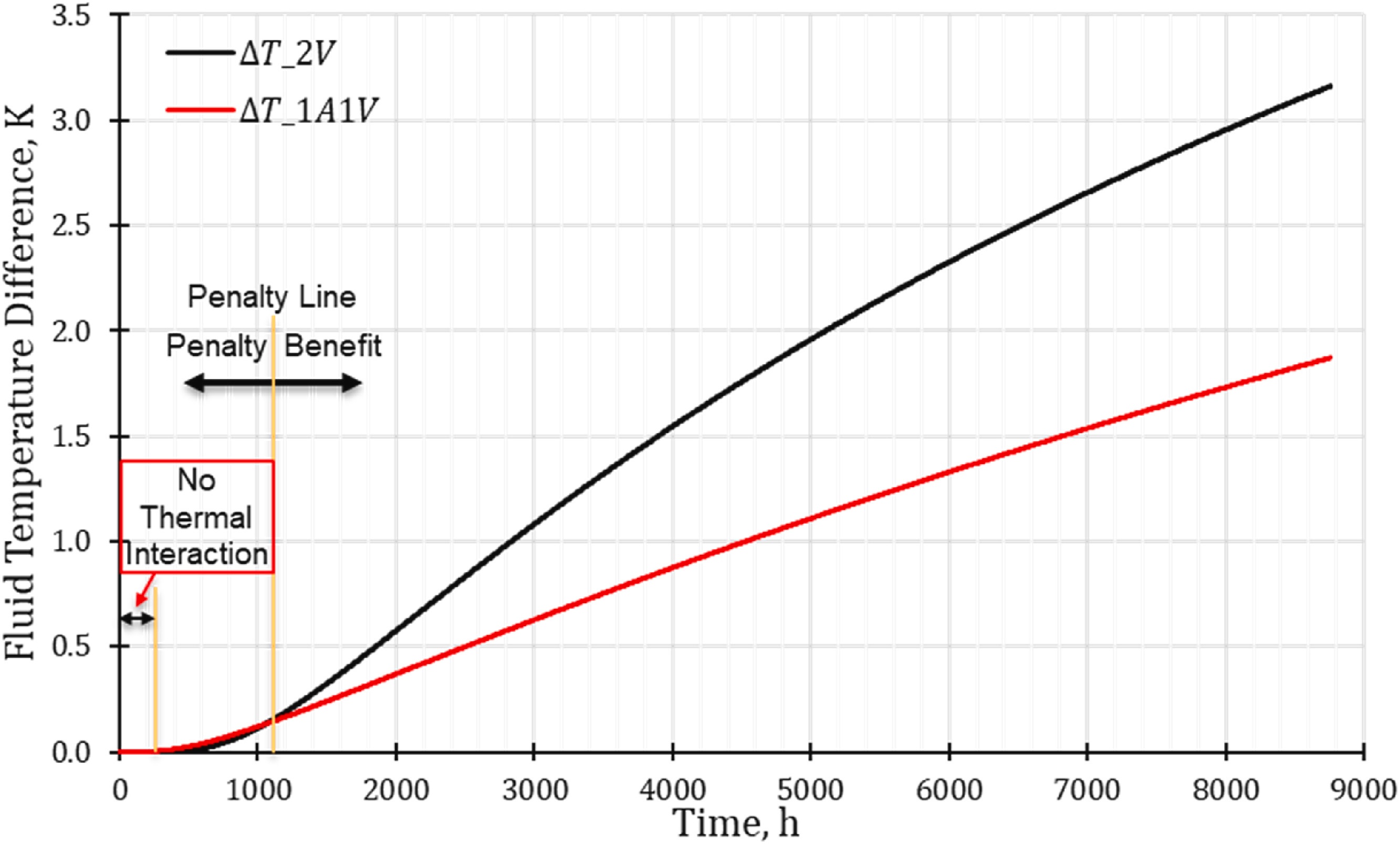
图 5. 在恒定热注入速率下,3 种配置的流体温度差。
衡量大型系统的性能
大多数比独栋住宅大的建筑都需要多个地埋管换热器。所需的换热器数量在设计时要考虑许多因素,其中之一就是在一年中最冷或最热的日子里为建筑物供暖或制冷所需的能量。Deacon 使用了4 个地埋管换热器来模拟不同数量换热器的影响,运行条件保持不变(每个地埋管的流量和入口温度相同,以此模拟不同配置下的传热性能)。
额外的地埋管换热器所带来的风险在于,当热源彼此距离更近时,热相互作用会加剧。他的研究使用了 3 种配置(图 6):
- 4V :4 个垂直式地埋管换热器的配置
- 3A1V-配置 1:3 个倾斜式地埋管换热器和 1 个垂直式地埋管换热器,且换热器之间有明显间隔
- 3A1V-配置 2:3 个倾斜式地埋管换热器和 1 个垂直式地埋管换热器,且换热器之间的间距极小
两种倾斜式配置都需要不到半平方米的地面面积,而 4V 配置则需要 25 平方米。3A1V-配置 2 最适合对地面面积较小的建筑进行翻新改造,而 3A1V-配置 1 则可能最适合地面面积较大的新建筑。

图 6. 4 个地埋管示例的三种配置的几何结构。
首先,模拟结果表明,当地埋管换热器的数量超过 2 个时,每个地埋管的性能就会下降。与 2 个地埋管的配置相比,每个地埋管的性能有所下降;流体温差尽可能小是最佳状态,但 10 年后的流体温差大于 1 K,而在 2 个地埋管的配置中,这一温差小于 1 K。性能下降的原因是热相互作用增加,以及由于地埋管分布更加密集,每个 地埋管可利用的地下空间减少。
关于 4 个地埋管换热器的配置,模拟结果显示,在 1 年的时间里,两种倾斜式地埋管换热器配置(3A1V-配置 1 和 3A1V-配置 2)的流体温差小于垂直式地埋管换热器配置(4V),这表明倾斜配置仍然具有更好的传热性能。在这两种倾斜式换热器的配置中,配置 1 全年的流体温度明显更低,由于间距增大,其性能更好。配置 1 在10 年后的流体温差约为 1 K,而配置 2 的温差约为 2 K。Deacon 推断,优化倾斜配置的布局将提升系统的整体性能。这些结果进一步证实了在整个模拟和研究过程中不断得出的结论。
通过模拟,Deacon 得出结论:通常来说,倾斜式地埋管换热器系统最适合改造项目,而垂直式地埋管换热器系统更适合新建建筑。当持续注入热量时,倾斜式地埋管换热器和垂直式地埋管换热器的初始性能相似,但随着时间的推移,由于地温场深层的地下体积更大,倾斜式地埋管换热器的性能显著提升。在 10 年的模拟时间内,倾斜式地埋换热器在制冷方面的表现也优于垂直式地埋换热器。根据这些结果可以确定,倾斜式系统更适合处理不平衡的能源负荷,也更善于利用地下体积。
“在地埋管位置和角度方面,如果你遵循几条通用规则,它们的性能实际上与传统系统非常相似。” Deacon 说道。
将供暖系统电气化以及将传统系统改造为地热能系统,历来成本高昂且难以普及,但仿真技术已帮助改变了这一局面。借助 COMSOL Multiphysics® 多物理场仿真软件,工程师能够逐小时估算地埋管在未来数十年内的性能表现。此外,仿真还能增强设计的可信度,并有助于降低出错的风险。
“现在我们既然有了这种建模仿真能力,就可以恰当地评估一个地埋管场的规模,降低成本,使设计方案更具可行性。” Deacon 总结道。
参考文献
- D.L. Deacon and M.F. Lightstone, “Three-dimensional analysis of multiple inclined borehole heat exchangers,” Renewable Energy, vol. 237, part B, 2024.
- Toronto Green Standard for New Low-Rise Residential Development, City of Toronto, Canada, Jan. 2017; https://www.toronto.ca/wp-content/uploads/2017/11/91f2-City-Planning-Toronto-Green-Standard-2017_LowRise_Standard.pdf
- T. Y. Ozudogru et al., “3D numerical modeling of vertical geothermal heat exchangers,” Geothermics, vol. 51, 2014.
- R. Beier et al., “Reference data sets for vertical borehole ground heat exchanger models and thermal response test analysis,” Geothermics, vol. 40, issue 1, 2011.
微流控系统通过比人类发丝更细微的微通道操控流体。作为该系统的核心组件,微泵在生物流体处理与微电子冷却等领域具有广泛应用。多物理场仿真技术使工程师能够以微观尺度所需的精度进行微泵设计。
编者注:本文初版发表于2015年7月17日,本次更新包含修订文本及新版本软件制作的模型图。
微泵设计面临的挑战
在微通道中对流体进行混合、分离和输送具有一定的设计挑战。工程师必须设计出满足微尺寸要求且性能优异的微泵。无阀泵凭借设计简单以及对生物材料更加温和的特性,常被选作微泵方案。然而,在没有传统泵的止回阀的情况下,维持单向流体流动具有挑战性。无阀微泵则依靠结构与流体之间的相互作用来实现单向流动。因此,无阀泵设计不适用于雷诺数较低的流体,或涉及黏性流体、小尺度或低流率的应用。COMSOL认证顾问Veryst Engineering 公司开发了一个模拟无阀微泵机理的模型,克服了这一设计限制。
在 Veryst 的模型中,微泵通过往复式驱动机构等方式,产生振荡流体运动。流体进入水平通道,通道两侧以倾斜角度布置可弯曲的微型阀瓣。这些阀瓣随流体运动发生弯曲,从而实现单向流动,无需采用阀门系统复杂的同步驱动机制。
通过仿真评估微泵性能
在此模型中,雷诺数设定为16,但也适用于雷诺数远小于1的情况。在 COMSOL Multiphysics® 软件中,通过 流-固耦合 接口设置输入振荡流以及微型阀瓣的物理属性,随后计算阀瓣的响应及其对流体流动的影响。全局常微分和微分代数方程 接口用于计算2秒泵送周期内随时间变化的净泵送率。
模拟从微泵的下冲程开始,即微泵将流体向下推入垂直腔室时。此操作会导致右侧阀瓣向下弯曲,同时左侧阀瓣向上弯曲。在此位置,左侧阀瓣阻碍流体流向左边,右侧流道被拓宽。这种结构自然地引导大部分流体向右流动,因为这是阻力最小的路径。
 在泵的下冲程期间测量流速大小、速度场和 von Mises应力,此时大部分流体被推向通道右侧。
在泵的下冲程期间测量流速大小、速度场和 von Mises应力,此时大部分流体被推向通道右侧。
在泵送上冲程期间,流体被泵入垂直腔室。上冲程产生的流动使阀瓣弯曲方向与下冲程时相反。这种变化不会改变净流方向,因为此时大部分流体从左侧入口被吸入流动通道。
 在 0.76s 时,流体被吸入,其中大部分流体在泵送上冲程期间从左侧入口流入。
在 0.76s 时,流体被吸入,其中大部分流体在泵送上冲程期间从左侧入口流入。
由于流动流体引起的阀瓣自然变形,这两个阶段均产生了从左向右的净流率。但在整个模拟时间内,此微泵机理维持这种流动的效果如何?
在为期 2 秒的测试中,从左向右的净泵送体积持续增加,在冲程速度达到峰值时净流率更高。这表明此模拟无阀微泵机理的模型能在如此低的雷诺数下有效工作,克服了许多无阀微泵普遍存在的局限性。
这种无阀微泵机理未来可能有许多应用,其中之一是用作流体输送系统。在这种应用中,微泵的工作机理可以从左侧的液滴储液池中吸取流体,并通过微流体通道将其输送到右侧的出口。
下一节
在这篇博客文章中,我们仅展示了一组模拟结果。通过自己动手实践 Veryst Engineering 提供的教程模型,您可以直观地了解无阀微泵在不同场景下的工作机理。
在设计换热器时,必须考虑传热速率、水力阻力和效率,对于某些应用,考虑结构完整性也很重要。然而,如果没有经济可行的制造方法,花费时间和资源来研究这些组件将是徒劳的。在整个设计过程中考虑设计和制造成本使换热器的开发成为一项艰巨的任务。这篇博客文章,我们将探讨使用形状优化和拓扑优化来应对这这类设计挑战的可能性。
形状优化
形状优化的过程与物理场无关,因此比拓扑优化更容易实施。需要注意的是,形状优化和拓扑优化均涉及大量设计变量,无论采用哪种方法,都必须使用梯度优化算法。当涉及大量设计变量时,基于梯度的优化方法显著快于无导数方法,因为它能高效利用敏感性信息指导每次迭代,而不是依赖耗时的采样或穷举所有可能解来寻找最优解的确定性优化方法。本文中示例采用的是移动渐近线(MMA)优化算法以及自动梯度计算方法。
首先,我们来看一个板式换热器的形状优化,然后探讨管壳式换热器中管道的尺寸设计。
对形状优化的更详细介绍感兴趣的读者,可查阅博客:电磁学中的形状优化:第 1 部分。
对于给定的驱动流率,可以通过对压降施加约束来限制换热器的水力阻力,但优化将倾向于对压降的最大允许值进行相应的设计,因此实际应用中的泵送功率和水力阻力是固定的。或者,可以施加压力驱动的流量,让优化过程选择泵送功率和水力阻力,这种方法计算成本更低,我们将重点探讨此选项。
考虑一个层流状态的板式换热器示例,其中通过改变板的形状使传热速率最大化,如下方动画所示。相较于初始的平板设计,优化后的设计将传热效率提高了30%。
优化后的板式换热器迫使流体绕流腔体角落,如根据温度着色的流线所示。请注意,在设计的灰色表面中,变形被放大了两倍。
现在,我们来看第二个示例,湍流状态下的管壳式换热器。同样,使传热速率最大,但这次允许管的尺寸和位置发生变化。在这个示例中,优化只能将传热速率提高 5%,这可能是由于设计自由度比前一个示例低所致。
 用根据直径着色的管表示的优化后的管壳式换热器。靠近中心的直径较小的管使管与管之间的流率变化减少。
用根据直径着色的管表示的优化后的管壳式换热器。靠近中心的直径较小的管使管与管之间的流率变化减少。
拓扑优化
使用密度方法进行拓扑优化,通过为每个计算单元指派一个设计变量来实现。在结构力学中,0 对应于空缺,1 对应于固体。
希望对拓扑优化有更深入了解的读者,可阅读博客文章:使用密度方法进行拓扑优化。
换热器拓扑优化的任务是确定哪个区域应该属于哪种流体,因此通常设计变量等于 0 对应一种流体,而 1 对应另一种流体(见参考文献1)。该策略可避免两种流体混合,前提是最终设计中不存在灰度值,即设计变量仅取 0 或 1,不包含中间值。该策略可以扩展用于考虑流体间的固体域,但本文将省略此部分。无滑移边界条件通过达西惩罚项施加,类似于其他流体拓扑优化应用中使用的策略:
\mathbf{F}_\mathrm{hot} &=&-\alpha(1-\theta) \mathbf{u}_\mathrm{hot}, \quad \mathrm{where} \quad \alpha(\theta)=\alpha_\mathrm{max}\frac{q(1-\theta)}{1+\theta},
式中, 和
分别表示热域和冷域的流速,通过不同的偏微分方程(PDE)求解。
表示抑制流速的最大阻尼系数,用于确保两个流速在同一时刻不会同时过大。
决定了设计变量场
中间值的阻尼系数,较小的值通常与灰度设计最优相关,而较大的值则会产生更多离散的明确分离的区域,从而获得物理上可实现的设计。
能量守恒通过对流-扩散方程求解,其中对流项取决于总速度场,由 的和给出。尽管该和式不明确依赖于设计变量,但在实际中,每个速度场在其对应的流体区域内占主导地位,因此流速仅在流体之间的过渡区域内具有可比性。
换热器通常在湍流状态下运行,但本文展示的拓扑优化结果仅限于层流状态,因为湍流模型需要解析边界层,而对于拓扑优化中使用的均匀网格,这会导致计算成本极高。
大通道具有较低的流体阻力,小通道则能提供良好的热交换效果。因此,理想的换热器拓扑结构应由交错排列的管道组成,这些管道在实际热交换发生的狭小区域内分支为细小管道。但是由于混合约束有效地固定了拓扑结构,这种结构在二维空间中无法实现。
在二维拓扑优化中,通过使两种流体之间的热交换最大,可以得到两根弯曲的平行管道。
在三维中进行拓扑优化的计算成本很高,因此在本文最后的示例模型中,通过施加镜面对称性将设计域缩小至原来的二分之一。此外,对流场施加旋转对称性,这样只需计算其中一种流体的流动。最后,目标函数同时考虑了传热速率和水力耗散。这两个变量均需最大化,因为对于压力驱动的流体,最大化水力耗散将使水力阻力最小。目标函数可通过极大极小值公式组合,但该方法计算成本过高,因此改用 p-范数代替:
&\approx& \left[(\kappa\phi_\mathrm{heat})^{-P}+\psi_\mathrm{cold}^{-P}+\psi_\mathrm{hot}^{-P})\right]^{-1/P},
式中,权重 用于控制各目标函数的相对重要性,
用于控制近似精度。这里展示的结果未将效率纳入目标函数(因为它会妨碍离散化设计),但初期可引入效率参数以引导设计趋向效率更高的极值点。
通过五个截面切片动态演示原始设计变量场,用于说明随着设计变量 的增加,优化结果逐渐趋向离散化的过程。
对优化后的结果进行平滑处理,以便能够通过显式几何表示对设计进行验证。如下方动画所示。相机位置固定,但设计结构略微透明,因此可以观察到结构内部的细节。 或者,您也可以探索下方的交互式模型文件,其中设计结构固定,相机位置可自由调整。图中仅显示了设计结构的一半,以便更清晰地观察内部的复杂细节。
优化后的换热器由两个相互交错的流体域构成,通过分支管道实现高强度热耦合,同时避免引入过大的水力阻力。
优化功能概述
这篇博客重点讨论了稳定流态换热器的优化设计,但其底层功能具有高度灵活性——基于梯度的优化方法同样适用于其他物理场问题,甚至可以将不同的物理现象结合起来,同时自动计算梯度以满足自定义的目标和约束条件。形状优化和拓扑优化接口可用于设置设计变量,探针可以简化约束和目标的设置。然而,约束和目标函数高度取决于具体的应用场景,因此建模过程的这一部分可能需要进行一些调试。最后,也可以执行考虑特征频率或瞬态问题的梯度优化。
对特征频率优化示例感兴趣的读者,可查阅博客文章: 通过形状和拓扑优化实现特征频率最大化。
关于热管理系统优化的网络研讨会
想要了解更多关于如何使用优化技术自动生成高性能的换热器和流体流动系统设计吗?欢迎参加 COMSOL 即将举行的热管理系统优化网络研讨会。此次网络研讨会将于美国东部时间 9 月 3 日星期三 15:00-15:45 举行。
参考文献
- P. Papazoglou, Topology Optimization of Heat Exchangers, master’s thesis, Delft University of Technology, 2015.
肺动脉狭窄(PAS)是指肺动脉狭窄导致压力增加并对心脏造成负荷的情况。除了 CT 和 MRI 等传统的成像方法外,计算模拟也能为理解血流动力学提供有价值的参考。在这篇博客中,我们将展示如何通过将狭窄视为多孔介质来模拟通过狭窄肺动脉的血液流动。这种方法可以帮助研究人员更好地理解动脉狭窄对血液流动的影响。从长远来看,它还可以帮助医生评估狭窄的严重程度,并决定是否需要进一步检查或治疗。
狭窄和血流特征
超声波、CT 和核磁共振成像等医学影像技术通过可视化解剖结构,针对不同患者的肺动脉狭窄提供有价值的见解。这些方法还可用于测量速度和流向等血流特征,例如利用超声波中的 多普勒效应 。计算模拟可以提供整个血管的动态压力、速度和应力的详细情况,是对上述方法的补充。通过将这两种方法相结合,临床医生和研究人员可以获得更加透彻的见解,从而优化诊断和治疗计划。
狭窄是指使血液流动受限的血管收缩,通常由斑块积聚引起。这种狭窄会导致湍流和压力增加。为了更好地理解这些效应,血液动力学研究人员使用数学模型来描述狭窄的形状,并分析其几何结构、位置和血液特性如何影响血流和压力。
 理想动脉中的流场,从左到右依次为轻度钟形狭窄、健康部分和严重不对称狭窄动脉。流线显示狭窄造成的湍流,颜色则表示压力水平,显示了狭窄情况下压力显著增加。
理想动脉中的流场,从左到右依次为轻度钟形狭窄、健康部分和严重不对称狭窄动脉。流线显示狭窄造成的湍流,颜色则表示压力水平,显示了狭窄情况下压力显著增加。
血液是一种非牛顿流体,这意味着其黏度会随着流动条件的改变而变化。这种行为受剪切速率和红细胞数量(血细胞比容)的影响,可以用不同的模型来描述:
- Carreau 模型—常用于表征动脉血流的剪切稀化效应,即黏度随剪切速率的增加而降低。
- Casson 模型—适用于低剪切条件,例如毛细血管血流,在这种条件下红细胞往往会聚集,从而使黏度增加
- Herschel-Bulkley 模型—考虑屈服应力,这在高血细胞比容条件下具有重要意义,因为在这种情况下,血液会抵抗流动,直到超过某个阈值才会开始流动。对于肺动脉等大型血管,Carreau 模型是合适的。由于此类血管的剪切速率相对较高,直径较大,血液在其中的表现更像是牛顿流体,尤其是屈服应力的影响很小,因此它计算简便,同时也能很好表征肺动脉中的血液,对二者进行很好地平衡。
将狭窄区域模拟为多孔介质
本文示例的肺动脉模型并非基于患者的真实数据,而是手动创建的(因为我们无法获得 CT 扫描或其他医学影像)。不过,仿真过程基本相同:如果有 CT 数据,可以用专业软件进行处理,并导出为 STL 面网格,然后导入 COMSOL Multiphysics® 软件进行三维仿真。
将面网格作为网格部分导入软件后,就可以通过在网格内引入新的表面来创建多孔狭窄域,来确定狭窄处的大小和位置。确定好之后,就能生成模拟域。应用四面体网格并沿动脉壁添加边界层,以确保该网格适用于血流仿真。
 导入的面网格(左)、引入的表面(中)和准备用于 CFD 分析的网格(右)。
导入的面网格(左)、引入的表面(中)和准备用于 CFD 分析的网格(右)。
要将血管狭窄描述为多孔介质,孔隙率和渗透率是关键参数。孔隙率代表狭窄区域的空隙比,而渗透率则量化了血液流经狭窄区域的能力。孔隙率和渗透率越低,说明狭窄越严重,进而导致大的压降并增加流动阻力。在上一篇博客中,我们探讨了如何在孔隙尺度上模拟多孔介质中的非牛顿流动,从而得出表观剪切速率的方法。现在,我们以这一想法为基础,应用表观剪切速率法对狭窄区域进行建模。这样,我们可以在表征狭窄对血流的影响的同时,避免解析狭窄的确切几何结构,从而使得在几何模型中改变狭窄区域的大小、严重程度和位置变得更加容易。
将血液模拟为 Carreau 流体
使用 Carreau 模型来描述血液的表观黏度,以反映其在不同流动条件下的剪切稀化行为:
该模型定义了在剪切速率为零 和无限
条件下的黏度,以及弛豫时间
和幂指数
。在自由流动区域,剪切速率为
,而在狭窄区域则由表观剪切速率 代替,表观剪切速率考虑了多孔结构对血液黏度的影响。
的确切形式取决于多孔介质,必须通过测量或孔隙尺度模拟来确定,例如使用第一节中的数学模型,并遵循上一篇博客中讨论的程序。不过,在此模型中,我们使用毛细管束方法对
进行近似计算,这里可以合理假设狭窄处的形状与毛细管类似:
表观剪切速率取决于孔隙率、渗透率和速度大小 。常数
考虑了迂曲效应,n 是 Carreau 模型中的幂指数。虽然这只是一个简化的近似值,但它能够分析狭窄对血液动力学的影响,并为医学诊断提供有价值的见解。
模型设置
该模型受 参考文献 1 的启发进行设置。为了模拟血流,我们在入口处采用了类似的瞬态速度((v_in(t)))。脉冲的形状通过插值函数定义,而插值函数又用于解析函数使其具有周期性。在出口处,我们设置了恒压条件。
 设置入口速度函数。图形窗口显示几何结构和应用设置。蓝色区域为狭窄区域。
设置入口速度函数。图形窗口显示几何结构和应用设置。蓝色区域为狭窄区域。
根据之前的模型,我们得到孔隙率 和渗透率
的近似值。这些数值代表了明显的狭窄,也与参考文献 1 中使用的数值一致。
为了给瞬态研究提供一个良好的起点,我们首先使用零时刻的入口速度进行稳态研 究,得到一个真实的初始流场,然后用上图所示的瞬时速度继续研究。为此,我们在入口处使用了v_in(try_catch(t,0)) 表达式。参数 try_catch(t,0)确保函数在瞬态步骤中使用当前时间,在稳态研究步骤中使用零时间。这种方法消除了对单独入口边界条件的需求——一个用于稳态研究((v_in(0),其中时间未定义),另一个用于瞬态模拟((v_in(t)))。
模拟结果
对有和无狭窄的血流模拟进行比较后发现,正如预期,狭窄近端压力明显增加。压力升高会导致动脉壁上的应力增加,可能造成血管损伤。此外,狭窄会引起下游更多的湍流,从而增加血栓形成的风险。
 健康动脉(左)和狭窄动脉(右)的流场,用颜色表示压力和最大压力的位置。
健康动脉(左)和狭窄动脉(右)的流场,用颜色表示压力和最大压力的位置。
量化狭窄严重程度的有效指标是定量肺压比(QPPR),即远端与近端的最大压力之比。QPPR 越低表明压降越大,因此狭窄越严重。该比值有助于评估狭窄对血流的影响程度。在该模型中,QPPR 约为 0.8。
下一步
这篇博客介绍了如何通过将狭窄视为多孔介质域来有效地模拟狭窄肺动脉中的血流。结合 Carreau 模型和表观剪切速率方法,这种模拟方法可以捕捉到压力升高和流动扰动等关键效应。模拟结果突出表明血管狭窄对血液动力学的重大影响。点击下方按钮,下载文中示例的教程模型和分步说明:
参考文献
- He, Fan, Wang, Xinyu, Hua, Lu, Guo, Tingting, Non-Newtonian Effects of Blood Flow on Hemodynamics in Pulmonary Stenosis: Numerical Simulation, Applied Bionics and Biomechanics, 2023, 1434832, 7 pages, 2023. https://doi.org/10.1155/2023/1434832
在 COMSOL Multiphysics® 软件的大多数功能中,都包含 弱约束 选项。这篇博客,我们将深入探讨什么是弱约束、为什么要使用弱约束,以及使用弱约束时需要特别考虑的事项。
章节内容
如何在 COMSOL Multiphysics® 中实施弱约束?
几乎在所有情况下,COMSOL Multiphysics® 中默认的约束类型都是逐点约束。逐点约束直接应用于自由度 (DOF),通常是网格中的一组节点。
在模型开发器的大多数标准约束功能的设置中,都有一个 约束设置 栏。在这个下列菜单栏中,您可以在两个不同的约束之间进行选择。一些功能的约束列表中可能包含第三个选项,即 Nitsche 约束。
约束设置 栏示例。
不过,默认情况下该栏并不显示。弱约束属于 “高级”功能。您可以在 显示更多选项 对话框中选择 高级物理场选项 来启用该栏。
拉格朗日乘子
由于弱约束是基于 拉格朗日乘子,我们有必要先从该主题的一些基本概念讲起。
拉格朗日乘子的概念是由数学家约瑟夫•路易•拉格朗日(Joseph-Louis Lagrange)在变分法研究中提出。在我们的博客诞辰快乐,约瑟夫•路易•拉格朗日中,您可以了解更多关于他的生平和工作。
一般的带约束最小化问题可表述如下:在一组约束条件 的约束下,求函数
的最小值。接下来的问题是,如何以一般的方式满足这些约束条件。对于简单约束(例如线性约束),可以显式地反解约束表达式并将结果代入
,从而减少未知数的数量。但这只是例外情况,而非普遍规律。
现在可以通过求解以下函数的最小值来解决问题:
式中, 是一组新的未知变量,即拉格朗日乘子。由于
为真解,因此很明显,
的最小值等于受约束
的最小值。但为什么会这样呢?
要找到函数的极值,需要计算所有变量的偏导数,并将它们设为零。在这个示例中,
和
因此,通过对方程组求关于拉格朗日乘子的偏导就可以恢复约束方程,也就是说,约束条件仍然有效。但是,第一组方程更为精妙。要理解对于特定值,为什么它们能确保获得正确的最小值,需要更详细的论证。值得注意的是,新方程现在还涉及约束函数的梯度。
如需完整且详细的解释和举例说明,请参阅:拉格朗日乘子。
有限元约束处理
考虑一个简单的线性静态有限元问题。最终离散矩阵形式可以写为
式中, 是刚度矩阵,
是自由度向量,
是节点载荷向量。为了能够求解此方程组(使刚度矩阵非奇异),必须已知至少一定数量的自由度值。例如,对于传热问题,至少需要一个温度,而对于三维固体力学问题,至少需要知道 6 个位移自由度。最常见的方法是直接输入该自由度的数值。此外还有其他选项,如热量传递分析中的对流边界条件或结构力学中的弹簧条件。
实际应用中往往会施加远超稳定性所需的约束,例如在整个边界上应用约束。只要存在一些受约束的自由度,就可以将方程组按如下形式进行划分:
式中,下标 a 表示激活的自由度,下标 c 表示受约束的自由度。矢量 包含受约束节点上未知的反作用力。这一术语来源于固体力学反作用力的概念。例如,在热量传递中,反作用力就是热通量。大多数情况下,约束节点上不施加任何载荷
,因为它们对解没有影响。
的值是已知的,例如
。在求解有限元方程时,最基本的处理方法是只求解激活的自由度。约束值的影响可以移到方程右侧,得到
求解简化后的方程组后,就可以使用以下方程在结果估计步骤计算反作用力
实际计算时,只需组装 矩阵,其余矩阵乘法运算可以在单元层面更高效地完成。
这种表述反作用力的方法假定问题是线性的,因此矩阵是常数。一种更通用的表述方式是,反作用力是残差计算的结果。对于激活的自由度,收敛解的残差很小。在受约束节点,残差较大,可以解释为反作用力。
在 COMSOL Multiphysics® 中,基本上 后验 是可以做到的使用 reacf() 算子计算与节点相关的反作用力。请注意,得到的值是集中的节点值而非连续分布场。根据单元中使用的形函数,这种节点值的分布可能不是很直观。不过,其求和结果在数值舍入误差范围内是精确的。
这种方法的缺点是,如果需要在计算中使用反作用力,它们就无法使用。
注:上述描述基于一般的有限元公式,是对 COMSOL Multiphysics® 内部实际处理方式的极大简化。实际上约束处理要复杂得多。例如,可能涉及非线性约束,或是连接不同物理场变量的跨场约束。
引入拉格朗日乘子法
现在,继续讨论离散化形式。为了不那么抽象,我们举一个固体力学的例子。对于线性问题,可以证明势能为
将 W 与位移最小化,就能得到之前使用过的普通方程组。现在,将所有约束条件与各自对应的拉格朗日乘子相乘后加入势能表达式:
为清晰起见,自由度向量分为无约束 DOF ( ) 和有约束 DOF (
) 。关键区别在于:新公式中将受约束自由度同样视为未知量。
为简单起见,假设受约束的自由度无外载作用。对各组变量求导后得到如下方程组:
利用第二行方程可以很容易地验证,拉格朗日乘子与上文介绍的节点反作用向量 完全相同。最后一行方程简单地说明了
。
如果原始刚度矩阵是对称的(通常是这种情况),那么这个新方程组也是对称的。但此表述存在以下局限:
- 与只求解激活的自由度不同,这种计算方法需要求解激活的自由度、受约束的自由度和拉格朗日乘子。
- 矩阵对角线存在零元素,部分线性方程组解法无法处理。
- 出于数值计算考虑,必须对方程组进行适当的比例缩放。原刚度矩阵元素的量级可能与单位值相差甚远。
尽管如此,该方法仍具显著优势:
- 反作用力值本身构成问题表述的一部分,不能仅视作结果量。
- 使用拉格朗日乘子时,强非线性约束条件的收敛效果会更好。
- 在逐点约束中无法使用时间导数。如果需要,使用拉格朗日乘子法是唯一的选择。
弱约束
弱约束条件同样基于拉格朗日乘子概念。不过,在离散化之前的数学描述中已经考虑了约束条件。
有限元公式的基础是使用基本方程的弱形式。在固体力学中,这也被称为虚功原理。计算公式如下:
式中, 是应力张量,
是应变张量,
是牵引向量,
是位移场。符号
表示变分算子。在 COMSOL Multiphysics® 中,它由
test() 和 var() 算子表示。符号约定与软件保持一致。
为简单起见,假设载荷(牵引力)只作用于边界。在更一般的情况下,也可能存在体积、边和点载荷。
为了使公式更加完整,需要在边界的某些部分设置位移的指定值,
在用选定的形函数近似位移时,该数学表达式将转化为有限元方程的离散化形式。
基于拉格朗日乘子的思想,现在可以通过添加一个额外项,将约束条件纳入弱表达式中:
式中, 是一个定义在约束边界上的拉格朗日乘子。假设
只是一个指定值(与解无关),那么最后一项可以扩展为三项,即
当使用有限元法将弱形式表达式转换为离散方程时,与位移一样, 使用形函数在单元上近似。原则上,两个场的形函数可以相互独立地选择,但这样会失去刚度矩阵的对称性(甚至会使矩阵变得奇异)。因此,通常使用与位移相同的形函数。组装后的方程组如下所示
矩阵 和
源自上述弱表达式中的第三项和第四项,只要位移和拉格朗日乘子使用相同的形函数,它们就具有对称性。
补充说明:矩阵
实际上与同一边界上单位面积质量分布的质量矩阵贡献相同。在 固体力学 接口中,可以使用 附加质量 节点给出这种质量分布。
为便于比较,我们重复上述对离散化系统应用拉格朗日乘子得到的方程组:
可以看出,结构类似,但单位矩阵被 所取代,右侧现在包含
,它是
的加权形式。
那么,这种修改会产生什么影响?指定自由度的节点值将不再与指定值完全一致。另一方面,节点之间的值在平均意义上将更接近给定函数 。
为了说明这一点,我们来看一个简单的传热示例,比较用标准逐点约束法和弱约束法得到的结果。
示例一:传热
使用二阶拉格朗日单元在单位正方形上以 2×2 网格求解一个二维传热问题。在最右边的边界上,温度设定为 sin(2*Y)。在相反的边界上,温度设为零。在其余边界上,没有任何边界条件,对应于无通量。温度选择指定正弦函数分布是为了避免二次形函数对其进行精确描述。
如果我们沿着右边界绘制温度曲线,两种方法之间的差异几乎重合,如下图所示。
在下图中,我们可以看到温度与其设定值之间的比较,这是一个更有趣的曲线图。
从上图可以看出,在节点点上,逐点约束与指定函数完全一致。而使用弱约束条件时,情况并非如此。
还存在一个或其他更好的解吗?第一个尝试是计算与给定函数相比的平均误差。结果如下表所示。
| 约束 | T-sin(2*Y) 的平均值 |
|---|---|
| 逐点约束 | 2.5*10-4 |
| 弱约束 | 3.6*10-7 |
事实证明,使用弱约束条件时,平均误差要小三个数量级。通过添加拉格朗日乘子场,指定值将在平均意义上尽可能地一致。为了证明这不是巧合,我们进行了一次参数扫描,将边的网格密度从 1 个单元改为 20 个单元。
需要强调的是,这些误差量级本身已经非常微小。对于任何合理细化的网格而言,上述对比主要具有理论研究价值。
在接下来的案例中,约束类型的选择将产生直观可见的影响。
示例二:杆模型
此例中,我们使用的是一根横截面为正方形的杆,它受到单轴拉伸。这是一个有两个域的装配体。一个域使用六面体单元网格划分,另一个域使用四面体单元网格划分。由于这是一个装配体,因此使用 连续性 条件将两个域连接起来。其结果是,网格在共同边界处 不兼容。
默认情况下,连续性是通过逐点约束来实现的,因此 目标 侧的每个节点都必须具有与 源 侧相应位置完全相同的位移。根据选择哪一侧作为目标,将得到不同的结果。
 使用逐点状约束时杆内的应力分布。在前景中,六面体单元构成目标侧,背景中则为四面体单元。
使用逐点状约束时杆内的应力分布。在前景中,六面体单元构成目标侧,背景中则为四面体单元。
由于两个域交界处的形函数不一致,应力场中存在明显的局部扰动。随着与连接处距离的增加,扰动会迅速消失。COMSOL博客:“圣-维南原理的应用和解释 ”中详细讨论了这一现象。
如果我们现在改用弱约束,结果会好得多。在下图中,应力采用了另一种标度。误差大约小了一个数量级。
结论表明,弱约束法能有效缓解非匹配网格连接时的应力扰动问题。
您可能会问,既然在传热示例中的影响如此之小,为什么在这个示例中两个公式之间的差异如此之大?答案是,指定温度是平滑的,可以用形函数进行合理近似。而在网格不匹配的情况下,每个单元面上的位移场都由各自的形函数表示,并不具有连续导数。现在,弱约束的平均效应变得更加重要。
Nitsche 约束
COMSOL Multiphysics® 中的一些约束功能允许使用第三种类型的约束实施方法:Nitsche 方法。本文不展开理论细节,它也是一种弱约束类型,但不依赖于拉格朗日乘子的使用。它没有增加额外的自由度。以下是将该方法应用于同一个杆示例时的结果。
Nitsche方法有多种变体可供选择。这里使用的是默认的对称方法。可以看出,源点和终点的选择不再重要,误差甚至比使用弱约束时更小。Nitsche 约束不仅涉及连接边界上的节点,还涉及与边界上一个面的单元相连的所有节点,因此提供了更多的灵活性。
Nitsche 方法的缺点是,在其默认(也是最稳定的)的实现中,会产生一个非对称刚度矩阵,这可能会大大延长求解时间。如果问题中还有其他效应导致非对称贡献,这一缺陷则可忽略,因为对称刚度矩阵的优势已不复存在。
术语说明
在 COMSOL Multiphysics® 中,当选择使用弱约束时,该功能表示”使用拉格朗日乘子进行约束”。在少数情况下,例如在约束单点或常微分方程 (ODE) 自由度时,拉格朗日乘子只是一个数值而非场量。在这种情况下,情况与上述离散情况相同:没有新的近似值,唯一的影响是可以直接获取约束力。(不过,你可能并不认为这是真正的弱约束)。
在某些情况下,特别是在结构力学接口中,调用拉格朗日乘子的公式时并没有明确提及弱约束。例如,刚性连接件 功能有一个名为 计算反作用力 的选项。
你可能会问为什么需要一个选项来获取反作用力。原因是对于该功能和其他类似功能,除了使用拉格朗日乘子外,没有其他方法可以计算反作用力。另一方面,总是使用这种计算方法可能会导致一些不明显的问题,这将在后文中讨论。因此,需要用户进行交互控制。
拉格朗日乘子的解释
上文提到,对于离散情况,拉格朗日乘子可直接解释为节点反作用力。这一特性更为普遍,并且不局限于有限元方法或固体力学。拉格朗日乘子代表执行约束所需的某种作用。通常,拉格朗日 代表一种能量。在这种情况下,拉格朗日乘子将与约束量在能量上共轭。
拉格朗日乘子的实际单位还取决于受约束物体的尺寸。对于固体力学,采用弱约束边界的拉格朗日乘子单位为 N/m2 = Pa。拉格朗日乘子场可以解释为为了保持指定位移而需要施加到边界上的牵引力场。但是,不应期望该域能准确表示约束处的局部应力场。不过,它在综合意义上是非常准确的。
为了说明反作用力的牵引力场,我们对下图中的短悬臂梁进行了研究。在固定端施加了弱约束。
接下来研究受约束端部的剪应力。根据分析解法,剪应力在横截面上呈抛物线分布。泊松比选择为零,以尽量减少约束效应。在给定的坐标系中,外加载荷会产生剪应力 σxy 和弯曲正应力 σxx。由于固定表面的法线位于 x 方向,牵引力分量 ty = σxy。因此,它应该用 y 方向上约束条件的拉格朗日乘子来表示。下图对这些结果进行了比较。
在所使用的网格分辨率下,应力和拉格朗日乘子均未精确反映真实解。存在一个显著差异:积分后,Y 方向总反作用力的相对误差在使用应力计算时为 3%,而使用拉格朗日乘子时为 2·10-12。
如果自行编写弱约束,拉格朗日乘数的物理意义可能因约束公式的不同而有强有弱。例如,假设需约束某点,使其变形后位于以原始位置为圆心、半径为 R 的圆周上。
以下展示了两种输入此类约束的不同方式:
在 弱约束 节点的设置中输入同一约束的不同方法。
这两种表达式都能以相似的迭代次数得到相同的解。然而,在第一种情况下,拉格朗日乘子的值很难解释。从量纲角度来看,它的单位是 N/m(因为它乘以单位为 m2 的约束条件)。在第二种公式中,它实际上是对径向位移的约束。计算出的拉格朗日乘子将是作用在支撑结构上的力。反作用力的方向并不明显,但会沿径向作用。因此,在物理上,该结构由一个无摩擦的圆形边界支撑。
不过,这个问题有两种可能的正确解—— 该点可能附着于圆周上的两个位置,本质上代表圆内侧或外侧的接触,最终解取决于初始条件。
使用弱约束时应注意的事项
约束冲突
在使用弱约束时最常见的问题是,若将其与标准逐点约束应用于同一自由度,二者无法共存。这种冲突可能导致”奇异矩阵””发现 NaN 或 Inf”等错误,甚至是完全错误的解。这种情况通常并非用户有意为之,但也可能在不经意间发生。
例如,如果在一条边界上使用弱约束,而在相邻边界上使用逐点约束。那么在公共边上就会出现冲突。通常,最简单的解决方法是将所有相连的约束条件转换为相同的表述(可能是弱约束条件,因为首先在某处选择它是有原因的)。有些约束的设置中还有 排除的边 和 排除的点 的部分。通过将冲突边添加到此类选择中,也可以解决问题。
在某些情况下,发生冲突的可能性并不明显。可能有一些约束条件是你没有想到的,因为它们或多或少是自动添加的。连续性 条件就是这样一种情况。
更微妙的是壳 接口中的情况,在 壳 接口中,每个节点都对旋转自由度(围绕壳表面法线的旋转)具有隐式约束。因此,如果在 壳 接口的任何对象上添加涉及旋转的弱约束(例如 固定约束 ),就会产生冲突。所有旋转约束(包括隐式约束)都必须改为弱约束。
拉格朗日乘子的单位
在大多数情况下,COMSOL Multiphysics® 中的拉格朗日乘子不带单位。这使得它们与几乎所有其他量不同。单位是隐含的,只能通过反作用力场的物理意义推断。如果需要在结果评估中频繁使用拉格朗日乘子,建议创建包含单位的中间变量。
添加一个带有单位的变量来表示拉格朗日乘子场。
变量缩放
有时,加入拉格朗日乘子会使非线性问题的迭代次数增加,甚至无法收敛。出现这种情况的最可能原因是容差处理不当。解决这一问题并确保容差得到正确处理的最佳方法是对拉格朗日乘子的自由度进行手动缩放。为此,请转到求解器序列中的 因变量 节点,并添加适当的缩放比例。缩放应提供拉格朗日乘子的数量级,即其代表的反作用力通量。
迭代求解器
如果使用迭代求解器求解线性方程组,拉格朗日乘子可能会引发一些问题。刚度矩阵的对角线上有零点,因此它不再是正定矩阵,大多数标准有限元公式都是如此。
因此,某些线性求解器和前置条件器不能用于求解弱约束问题,即共轭梯度迭代求解器和 SOR 类前置条件器和平滑器。您可以尝试另一种迭代求解器,并使用以拉格朗日乘数作为 Vanka 变量的 Vanka 算法,或者使用不完全 LU 因子化算法作为预处理器。
对于多物理场问题,一种可行方法是采用分离式求解策略;若模型规模允许,还可对涉及拉格朗日乘数的场使用直接求解器。
拉格朗日乘子自由度的奇异性
将标准约束条件转换为弱约束条件时,在数值上会表现良好。但是,如果编写自己的非线性约束条件,或使用约束变量的某些表达式,那么刚度矩阵的拉格朗日乘子部分可能会出现奇异性。
在上文使用的非线性约束示例中,当节点被约束移动到其原始位置周围一圈时,其原始配置实际上会失效。
这里的约束表达式实际上是一个以节点为中心的抛物面,因此当 u = v = 0 时,其梯度为零。
作为替代方案,您可以在拉格朗日乘子的自由度中添加一个人为的”刚度”。在上面的例子中,可以将表达式扩展为:u^2+v^2-R^2+1e-6*lm*(u^2+v^2 < 0.01*R^2)
拉格朗日乘子变量的名称为 lm。由于采用布尔表达式,额外的贡献只对小位移有效,因此不会影响真正的解。其作用是在刚度矩阵的对角线上放置一个小数值,以避免初始奇异性。
我们在下一篇博客的"弱约束条件"部分也使用了同样的方法:如何在仿真中设置边界条件。在该部分中,出现奇异性的原因是边界中只有随时间变化的部分具有指定值。在边界的其余部分,拉格朗日乘子的自由度仍然存在,但没有定义它们的方程。
扩展资源
COMSOL Multiphysics® 中的弱约束是强大的模拟技术,但要成功运用它们,需从数值角度理解其底层机制。
如果您想了解更多有关弱约束的信息,也可以查看以下博客:
据国际食品信息委员会(参考文献 1)报道,由于食品召回事件和有毒成分报道的增多,消费者对食品安全的信心在 2024 年降到了历史最低点。因此,食品和饮料行业的公司比以往任何时候都更需要保证其产品的安全性。食品行业的公司借助建模和仿真能够优化其食品检测、灭菌、加热和包装流程,同时最大限度地减少浪费。阅读这篇博客,了解在 COMSOL 用户年会2024上展示的5个食品行业的仿真案例。
1. 评估细菌致死率
Fortune Business Insights 最近一项研究(参考文献 2)显示,消费者对保质期长且易于储存的罐头食品的需求多年来一直在稳步增加,并且这一趋势预计还将持续。食品灭菌对生产商来说非常重要,因为过程中的任何错误都可能导致有害甚至致命的细菌进入消费者的食品。COMSOL 认证咨询公司 BE CAE & TEST 使用 COMSOL Multiphysics® 软件中的 App 开发器开发了一款定制仿真 App,用于估计灭菌过程中渗透进罐头食品内部的有效热量,从而评估细菌致死率。该仿真 App 可以帮助食品工程师使用精确的多物理场模型分析罐头食品安全,且无需学习如何使用仿真软件。
在仿真 App 中设置分析时,食品工程师可以轻松地从几种基本形状的容器三维几何中进行选择,或者导入自定义的几何图形;选择豆类、玉米和金枪鱼等各种类型的食品;指定热处理方法。如果没有特定食品热物理性质的参考数据,也可以通过输入其营养成分,包括碳水化合物、蛋白质、脂肪、纤维和灰分(矿物质含量)的百分比来轻松计算。还可以通过该 App 导入实验参考数据,获得随时间变化的蒸馏温度曲线,或通过指定加热坡度、热稳定阶段和最终冷却温度和持续时间来定义温度曲线。
 BE CAE & TEST 用于评估罐头食品中细菌致死率的定制仿真 App,其中自定义的几何图形是一个装有金枪鱼的长方形锡罐。
BE CAE & TEST 用于评估罐头食品中细菌致死率的定制仿真 App,其中自定义的几何图形是一个装有金枪鱼的长方形锡罐。
通过在自定义输入框中输入感兴趣的数据,食品工程师可以使用该仿真 App 在瞬态分析过程中计算随时间变化的温度,用于确定热渗透如何影响各种罐头食品中的细菌致死率。有了这些信息的支持,他们就可以优化食品灭菌流程,降低有害细菌进入食品的风险。
了解有关他们的工作和这个仿真 App 的更多信息, 请查阅:分析灭菌过程中细菌致死率的 COMSOL 仿真 App
2. 优化通心粉干燥条件
对于意大利面生产商而言,面食干燥过程需要进行一系列耗时耗力的实验来确定最佳操作参数,从而获得稳定、优质的产品。全球最大的意大利面生产商 Barilla 与意大利 Calabria 大学合作开发了一个模型来预测意大利面干燥过程中的温度、水分分布和结构变化,进而优化干燥过程,确保产品质量并最大限度地减少能源消耗。
烘干意大利面所需的时间差异很大,具体取决于两个参数:
- 空气温度( 40°C ~ 90°C) 和相对湿度(40% ~ 85%)
- 气流速度波动
该团队采用双域建模方法开发了一个模型,用于预测在湍流空气条件下干燥过程的温度和水分分布。该研究团队在模拟中使用了一个二维几何图形来表示一根”tortiglione “意大利面。
他们使用有限元法将传热和传质方程耦合起来,并对模拟进行参数化以反映典型的工业条件。该模型考虑了食品在干燥过程中的收缩。总体而言,研究团队的仿真预测结果与干燥过程的实际结果相比,平均相对误差小于 9%。
收缩的影响和模型验证结果。
了解更多有关该团队工作的信息,请查阅: “Comprehensive analysis of the transport phenomena developing inside a pasta drying chamber
3. 分析液体食品包装的降解情况
液体食品包装必须能安全地保存食品,且不会让包装在接触液体时发生降解。这种包装通常由核心支撑材料纸板、保护食品的聚合物保护层和通过感应加热(IH)密封包装的薄铝层构成。世界领先的食品加工和包装解决方案商利乐公司(Tetra Pak)的一个团队对感应加热过程中的包装材料响应进行了建模和仿真,以了解不同属性如何影响包装的材料性能。
他们建立了自己的模型并模拟了感应加热-密封过程纸板中热量和质量传递的相互作用。该模型以铝层为边界条件,考虑了通过AC/DC磁场的涡流。他们使用多物理场耦合仿真来确定纸板的干燥如何受到内部气体压力的影响,以及纸板不同区域的干燥程度。仿真结果表明,当纸板的初始含水率较高且密度较低时,由于水分引起的降解较少,蒸汽更容易逸出,这一点在纸板最干燥的顶角处可以观察到。仿真结果还表明,模型预测与实验数据非常吻合。这些发现使利乐公司能够进一步优化其聚合物模型,从而减少材料浪费。
了解有关他们工作的更多信息,请查阅:模拟感应加热密封过程中纸板的质量和热量传递耦合。
4.改善烤箱气流
为了以最低的成本精确计算烤箱腔内的气流,烤箱制造商 UNOX SpA 正着手寻找最有效的仿真策略。作为这项工作的一部分,该团队使用 COMSOL Multiphysics® 软件研究并比较了各种流体动力学仿真策略。
该研究包括三个步骤。首先,他们使用一个管道和带冷冻转子的风扇的简化域进行研究,该研究的计算成本较低,并且可以进行实验验证。接着,他们对实际烤箱风扇的复杂几何形状进行了完整模拟,包括冷冻转子和传热研究。该模拟非常精确,但计算量也很大。最后,他们进行了与前一项类似的分析,但在不模拟旋转风扇的情况下施加了速度曲线,从而降低了计算成本。
研究团队对这三个步骤的结果进行了分析,发现第三种策略能以最少的计算时间获得非常准确的结果,因此是其工作最有效的方法。
了解更多有关他们工作的信息,请查阅:烤箱中的流体动力学仿真:平衡精度与计算效率
5.应对巴氏杀菌的挑战
含水量低的食品可能会因耐热微生物的污染带来安全问题,因此蒸汽或热空气等典型的巴氏杀菌法无法奏效。微波加热可作为一种替代方法,但由于干燥食品的介电特性较低而面临一定挑战。来自工业微波和射频应用领域的全球领先企业 SAIREM 和法国高等教育机构 Oniris Nantes 的一个团队合作开发了仿真模型来研究这一过程的复杂性。
他们模拟了用 915 MHz 单模微波加热器加热石英管中辣椒粉的过程,并分析了管内的电场分布和局部温度。研究团队模拟了几组不同的介电特性值,结果显示,与损耗因子相比,介电常数的不确定性导致了更大的温度变化。他们还实际测量了辣椒的热物理性质,包括密度、热量和热导率,发现二者结果非常一致。要准确预测生产安全食品所需的温度,精确测量含水量低的食品介电特性非常关键。
 在工作频率为 915 MHz 的微波腔内加热的石英管模型中的红辣椒粉末,显示了由于介电常数的不确定性导致的温度差异。
在工作频率为 915 MHz 的微波腔内加热的石英管模型中的红辣椒粉末,显示了由于介电常数的不确定性导致的温度差异。
了解有关他们工作的更多信息,请查阅:介电常数对 915 MHz 微波腔中低水分食品巴氏杀菌的影响
多物理场仿真保障食品安全
这篇博客,我们了解了食品和饮料行业的工程师如何使用多物理场仿真和仿真App分析和优化与食品安全相关的产品和流程的5个真实案例。当然,这些案例只是这一领域的简单仿真。如需获取更多灵感,请至 COMSOL 官网查阅 食品和饮料行业的应用专题。
参考文献
- Consumer confidence in food safety hit a record low in 2024. (2024, September 19). International Food Information Council. https://ific.org/media-information/press-releases/food-safety/.
- The canned food market in the U.S. is projected to grow significantly. (2025, April 14). Fortune Business Insights. https://www.fortunebusinessinsights.com/canned-food-market-103258
过去 50 年间,人类探索和机器人探测极大地扩展了我们对地球伴星的了解。然而,我们对月球仍有许多需要探索的地方,月球科学的一个重要方面就是了解月球的热行为。印度物理研究实验室的 Durga Prasad 博士通过建立首个此类热物理模型,将仿真与实验室实验相结合,在理解月球表面和地下温度的空间和时间变化方面取得了重大进展。
我们为什么需要了解月球表面?
辐射会对载人航天飞行产生不利影响,使宇航员致癌,月球表面的热循环会导致建造的任何栖息地产生热疲劳。因此,对月球热动力学的研究有助于选择合适的着陆点,确定设备和栖息地的稳定热条件,优化发电和热管理系统,从而为任务规划提供帮助。此外,类似的研究在帮助科学家确定水冰等潜在资源的位置,以及制定开采策略方面也发挥着至关重要的作用。这些信息还有助于深入了解月球的地质、月壤特性和内部过程,助力科学研究和我们对天体更广泛的了解。
 图 1. 一张满月照片。图片由 Gregory H. Revera 提供,获 CC BY-SA 3.0许可, 通过 Wikimedia Commons 共享。
图 1. 一张满月照片。图片由 Gregory H. Revera 提供,获 CC BY-SA 3.0许可, 通过 Wikimedia Commons 共享。
为了进一步了解月球的温度分布和热行为,Durga Prasad 博士团队着手建立一个全面的三维热物理模型,以帮助预测实际的热行为,模拟地球物理问题,并协助规划未来月球上的实验。
开发月球表面的热物理模型
Durga Prasad 博士于 2022 年发表在 Earth and Space Science 上的一篇论文中详细介绍了随后所做的努力。当时,关于月球热物理行为和热流的现有知识和测量都很有限。已知的信息都只针对赤道和中纬度地区。据了解,月球表面由导热系数较低的多孔层和密度较高的致密层组成,这对地表和地下的温度有显著影响。月球的地形在热量传递中也起着至关重要的作用,本研究也考虑到了这一点。
为了加深理解,Durga Prasad 博士建议采用实验室实验和数值仿真作为可能的研究方法。这项分析旨在通过推导月球表面和地下温度来预测月球的实际热行为,为开发这样一个综合模型迈出第一步。
模型开发过程包括创建两层横截面,用于探索温度和热通量的行为。研究人员在 COMSOL Multiphysics® 软件环境及其附加产品传热模块中使用了三维有限元方法。这种方法能够准确地表征月球表面的复杂几何形状,并确保模型适用于小尺度到大尺度的模拟。
考虑关键参数和地形的影响
为了准确模拟月球表面和地下的热物理行为,必须考虑适当的参数值和边界条件。密度、热导率和比热容等参数并非恒定不变,而是相互依存的。包括密度在内的关键参数是根据以往研究得出的关系式定义的。导热系数和比热容是通过温度相关函数(理论曲线拟合)推导出的。此外,还使用了一个半正弦函数来表示太阳热通量的昼夜变化。
Durga Prasad 博士模型的一个重要方面是纳入了月球的地形变化及其对热量交换和热物理行为的影响。传统的一维模型提供了一个全球视角,但无法模拟局部和区域尺度的现象。通过数字高程模型(DEM)数据纳入月球表面的实际地形(图 2),可以更真实地反映月球的热行为。
 图 2. (a) Taurus–Littrow 山谷和阿波罗 17 号着陆点 (b) 区域尺度模拟所考虑的关注区域 (c) 为局部尺度模拟创建的人工 DEM 几何图形 (d) 划分网格的几何和 y-z 切面。
图 2. (a) Taurus–Littrow 山谷和阿波罗 17 号着陆点 (b) 区域尺度模拟所考虑的关注区域 (c) 为局部尺度模拟创建的人工 DEM 几何图形 (d) 划分网格的几何和 y-z 切面。
 图 3.基于模型计算的月球日选定时段的局部尺度表面温度三维图。
图 3.基于模型计算的月球日选定时段的局部尺度表面温度三维图。
Durga Prasad 博士开发的模型是独一无二的,也是全球首个此类模型,它成功地考虑了地形变化,从而能够表征月球表面不同位置的温度分布。团队利用实验室实验和阿波罗 17 号的现场数据对模型的结果进行了验证,证实了月球表面热结构(包括最上层的厚度)作为影响月球表面和地下温度变化的关键参数的重要性。
未来的月球研究
Durga Prasad 博士的研究标志着我们在推进对月球局部热物理行为的理解,以及对未来月球探索任务规划的针对性调查方面迈出了重要一步。通过建立一个完整的三维热物理模型,他对月球表面和地下的温度变化提出了宝贵的见解。这项研究对未来的月球探索任务具有实际意义,有助于选择合适的登陆点、优化热管理系统和促进资源利用。此外,该模型还加深了我们对月球地质、月壤特性和内部过程的了解。
参考文献
- K.D. Prasad, V.K. Rai, and S.V.S. Murty, “A comprehensive 3D thermophysical model of the lunar surface,” Earth and Space Science, vol. 9, 2022; https://doi.org/10.1029/2021EA001968.
延伸阅读
番茄酱、血液等非牛顿流体会展现出与应变速率相关的特性,这使得模拟通过多孔介质的流动变得复杂。多孔材料的复杂结构,如通道、停滞区和孤立孔隙会导致流体特性各不相同。在没有通用理论的情况下,常常需要通过测量或孔隙尺度仿真的方法开发出特定的流体-材料组合模型。在这篇博客中,我们演示了如何利用仿真或测量结果开发出一种均质化方法,用于模拟非牛顿流体在多孔结构中的流动。
非牛顿流方法
日常生活中某些流体会表现出反直觉特性。一个众所周知的例子就是番茄酱,刚开始它会顽固地附着在瓶壁,然后突然在整个盘子上铺满红色的酱汁。当黏度随着剪切速率的增加而降低时,就会出现这种被称为“剪切稀化”的现象。类似地,大多数聚合物也会出现这种现象。较少见的是剪切增稠流体,即黏度随剪切速率的增加而增加。一个著名的例子是 Oobleck(一种玉米淀粉悬浮液),其黏度会随剪切速率增加,甚至可使人在其表面快速行走时如履平地。
剪切速率表征相邻层间流体的相对运动速度,取决于流体速度场 和流道曲率引起的梯度变化,其数学表达式为:
其中, 为应变率张量 。在多孔介质中,错综复杂的孔隙分叉和汇合导致速度和剪切速率快速变化,从而引起孔隙空间内黏度的显著变化,如下图所示的 Carreau 流体流经不规则孔隙结构的示例。
 流线图展示了 Carreau 流体的黏度分布:剪切速率较高的狭窄通道展现出较低的黏度,而剪切速率较低的较宽区域则维持较高的黏度,流线突出显示了孔隙结构对流体行为的影响。
流线图展示了 Carreau 流体的黏度分布:剪切速率较高的狭窄通道展现出较低的黏度,而剪切速率较低的较宽区域则维持较高的黏度,流线突出显示了孔隙结构对流体行为的影响。
这种动态黏度变化给非牛顿流体流动仿真带来挑战。为实现更大尺度的模拟,我们需要有效的升尺度方法,将孔隙尺度行为转化为宏观流动特征。
孔隙尺度模型的升尺度转换
对于大尺度应用,在孔隙尺度上模拟非牛顿流体的流动是行不通的,因此必须进行升尺度处理。其中一种方法涉及定义表观黏度 ,本质上是会产生与非牛顿流体相同压降的(恒定)黏度(参考文献 1)。
根据达西定律,表观黏度可以表示为 :
(1)
式中, 是多孔介质的渗透率,
是速度,
是压力梯度。这些数值可以通过测量获得,也可以像我们的示例一样,通过代表性体积单元(RVE)的孔隙尺度模型获得。(本征)渗透率是多孔基质的一种性质,仅取决于孔隙大小、形状和连通性,其计算方法可参考这篇博客及相应模型。
在已知结构渗透率的前提下,令 Carreau 流体通过该多孔结构,其表观黏度或有效黏度的定义如下
(2)
其中,参数 和
分别为零剪切速率和无限剪切速率情况下的黏度,
为弛豫时间,
为幂律指数。为了进一步证明升尺度方法的必要性,我们将相同的 Carreau 流体通过具有相同孔隙率和渗透率的不同多孔结构,并施加相同的压降。不出所料,剪切率受流道曲率的影响。由于不同结构的流道不同,剪切速率也不同,因此,我们测量或使用方程(1)中的方法进行计算的结果也不同。
 在相同的边界条件下,具有相同孔隙率和渗透率的不同多孔结构展现出不同的表观黏度,这突出表明了流体和结构对剪切速率的影响。
在相同的边界条件下,具有相同孔隙率和渗透率的不同多孔结构展现出不同的表观黏度,这突出表明了流体和结构对剪切速率的影响。
在构建多孔结构的升尺度模型时,需要一个剪切速率的表达式,因为不能仅根据达西速度直接计算剪切速率。我们将这个表达式称为表观剪切速率 ,然后将其用于方程 (2)中。
对于不同应用场景,存在多种计算公式。一种常用的形式是:
(3)
式中,孔隙结构的影响用校正因子 表示。虽然可采用现有经验关系式确定
,但将
与测量值或模拟数据进行拟合可以获得更精确的结果。
计算和验证校正因子
校正因子可通过 COMSOL® 系统内置的方法确定。首先,利用方程 (2) 计算表观剪切速率 , 同时计算
项,我们称之为归一化速度。再根据方程 (3) 计算出
。虽然通常可以假定
在一定的压降范围内保持不变,但必须注意的是,它可能会因流动模式的变化(如湍流的发生)而变化。
本案例模拟了 50—5000 Pa/m 压降范围内的流动,COMSOL® 将计算结果输出到数据表,随后通过 最小二乘 拟合函数 对方程 (3) 进行参数拟合以确定 值。
该方法不仅支持孔隙尺度模拟数据,也可直接采用实验测量数据进行拟合验证。
为了验证这种方法,我们可以根据 Brinkman 方程建立一个均质化模型,并对结果进行比较。如果结果一致,则证明了近似方法的准确性和可靠性。
Brinkman 方程 接口和 达西定律 接口现在支持使用表观剪切速率法(包括热效应)模拟非牛顿流体流动,也就是说您可以在 6 种常用的非牛顿本构关系中进行选择。此外,您还可以输入自定义校正因子或选择毛细管束方法,该方法提供了另一种适用于毛细管束状多孔介质的 描述。下图是 COMSOL Multiphysics® 用户界面的截图,显示了流体属性设置窗口。
下图显示的结果表明,表观剪切速率法提供了准确可靠的预测。
下一步
由于流体特性与孔隙结构之间存在复杂的相互作用,模拟多孔介质中的非牛顿流体流动具有独特的挑战性。将孔隙尺度模拟或测量结果与升尺度技术相结合,可以得到精确的宏观模型。多孔介质流动接口目前支持表观剪切速率法,提供了一种考虑动态黏度变化和结构影响的可靠方法。
想自己建立非牛顿流体在多孔介质中的流动均质化模型吗?COMSOL 案例库中提供了 MPH 文件和分步说明,欢迎下载:
在后续博客中,我们将以狭窄肺动脉中的血液流动为例,展示表观剪切速率法在真实生物力学场景中的应用。
参考文献
- N. Zamani, I. Bondino, R. Kaufmann, A. Skauge, “Computation of polymer in-situ rheology using direct numerical simulation”, Journal of Petroleum Science and Engineering, Volume 159, 2017; https://doi.org/10.1016/j.petrol.2017.09.011.
Jan Czochralski 在研究金属结晶的速度时,将装满熔融锡的热坩埚放在桌子上冷却。他专心致志地工作,不小心把笔插入了熔融的锡里,而不是墨水瓶中。注意到自己的失误后,Czochralski 把笔拔了出来,却发现笔尖上挂着一条凝固的金属丝……
直拉法背后的历史
后来,Czochralski 证明了这种凝固金属是单晶体。将近 110 年后,他的简单失误被公认为直拉法奠定了基础。该方法是制备单晶硅的最重要方法之一,而单晶硅是一种广泛应用于电子产品制造的材料。
如今,直拉法采用的工艺与 Czochralski 意外的钢笔蘸取过程类似。首先,在坩埚中熔化高纯度的半导体级硅。然后,加入掺杂的杂质原子,使硅掺杂变成正型或负型硅。接着,把固定在一根棒上的籽晶浸入到熔化的混合物中,并在氩气的惰性气氛里小心地向上提拉,同时进行旋转。最后,熔融物会在籽晶上形成一根大的圆柱形单晶锭。
 直拉法的各个阶段。这张照片已进入公有领域,通过 Wikimedia Commons 共享。
直拉法的各个阶段。这张照片已进入公有领域,通过 Wikimedia Commons 共享。
Czochralski 探索了使用锡、铅和锌等金属制造晶体的方法,并于 1917 年发表了有关该方法的论文。这篇论文和方法一经发表便引起了人们的极大兴趣,但直到 20 世纪 40 年代末,这种方法才成为如今的主流技术。这在很大程度上要归功于贝尔实验室的研究人员,他们重新发现了这种方法,并利用它生产硅和锗晶体以开发半导体。从那时起,直拉法就成为半导体工业的基石。

波兰化学家Jan Czochralski,1929 年在华沙理工大学担任教授时的照片。这张照片属于公有领域,通过 Wikimedia Commons 共享。
直拉法是制备单晶硅(mono-Si)晶锭最常用的方法。该方法可以制备出长达 2 米的晶体锭,之后这种晶体锭可被切割成标准尺寸的晶圆。这些晶圆可用于制造集成电路,在光伏领域则用于制造太阳能电池。在这篇博客中,我们将探讨如何使用 COMSOL Multiphysics® 软件模拟保护气体流动和对流传热,以维持晶体生长界面所需的温度梯度。
典型晶体生长炉的模型定义
通过精准调控加热功率、拉速和晶体旋转速率,可以有效控制晶锭的形状,尤其是直径。可以在原型阶段对这三个因素进行调整,但必须使用昂贵的物理材料。作为这些实验的补充,建模和仿真可用于虚拟复制、监控和更改设计,从而减少所需的物理实验次数。
查看在软件中建立的热传导(左)和热辐射(右)模型。
直拉法晶体生长炉的热分析教程模型模拟了上述过程。该模型的几何结构包括一个装有熔体的石英坩埚和一根位于熔体表面中间的晶棒,二者均放置在生长炉内。在生长炉内,氩气流冷却晶棒,以维持所需的温度梯度,并将挥发性物质排出炉外。炉内放置了一个石墨加热器,用于维持稳定的温度。坩埚和晶棒均以 5 r/min 的速度旋转,但方向相反。上述过程的整个几何结构具有旋转对称性,因此可以在 COMSOL Multiphysics® 中使用二维轴对称模型创建。
假设热传导是主要的传热机制,对熔体、晶棒、石墨加热器和炉壁的热传导进行模拟。炉内表面之间的热传导由表面对表面辐射模型计算。炉内氩气的非等温流动采用弱可压缩流假设进行建模,同时将 k-ε 湍流模型和湍流中的热传递相耦合。晶棒和坩埚的旋转则使用滑移壁条件描述。
此模拟的重点是研究保护气流和对流传热,找出维持晶体生长界面所需的温度梯度和最佳参数。
使用COMSOL模拟的晶体生长炉模型。
在模型几何结构内部,石墨加热器的功率为 310 kW,保护性氩气的引入速度为 100 L/min。炉压保持在 2500 Pa。坩埚以 5 r/min 的速度正向旋转,晶体棒以 5 r/min 的速度逆向旋转,从而产生有效晶体生长所需的扭转运动。这种熔炉的旋转速度远高于拉速,因此本模拟忽略了拉速。
结果讨论
在模型中,我们进行了两步研究。第一步是求解稳态流动方程,为随后的瞬态研究步骤建立良好的初始条件。在瞬态研究步骤中,流动方程和传热方程是完全耦合求解的。
流场
仿真计算得出的流场显示,晶棒表面附近的流速最大。热屏和晶棒之间存在一个回流区,该回流区主要由热屏高温产生的浮力驱动形成,来自入口的轻微向下流动也对其产生一定影响。这种高速运动有利于有效散热,从而在晶棒内形成明显的温度梯度。
坩埚和加热器之间的水流向下流动,这与直觉相反,因为人们可能会认为这一区域会产生烟囱效应。但实际上这种效应发生在加热器外部,即加热器和炉壁之间,那里的水流主要是向上流动的。
值得注意的是,炉内自由对流的影响比氩气的入口和出口流动的影响更为显著,后者在图中几乎无法辨别。如果没有模型,预测整个流场将非常困难。
温度
我们的研究表明,熔体与晶棒接触面的平均温度在大约 400 分钟后达到稳定状态。熔化温度(Tm=1414 °C)等值线靠近该接触面,见下图中的 1415 °C 等值线。晶棒与熔体接触点的温度在 1403—1407.5°C 变化,最高温度出现在晶棒的中部,接近于 1414 °C 的实际熔化温度。温度沿晶棒高度方向逐渐降低,在 Z 方向上呈现出 500—100 °C/m 的温度梯度。这表明氩气流对单晶棒进行了有效冷却。
左图:突出显示了 600 分钟时平均温度的模型图。右图:晶棒与熔体接触面的温度分布。
晶体炉模型的扩展
借助上述仿真模型,我们将晶体和熔体模拟为固体,并在设计阶段进行了热分析。该模型既可以实现这一目标,也可以进行扩展。例如,您可以对其他加热方式(如感应加热)进行模拟。更复杂的扩展可能还包括重点模拟熔体中的流动及其内部的自然对流、表面对流(马兰戈尼效应)和强制对流(磁性流体)。您还可以使用 相变 接口查看从熔体到晶体的相变,以及晶体潜热和拉力的凝固过程。虽然本演示中忽略了晶体提拉速度,但您也可以在壁边界条件中设置该速度,即切向的移动壁速度。
动手尝试
想自己亲自动手尝试模拟这个 Czochralski 晶体生长炉吗?COMSOL 案例应库中提供了相关的 MPH 文件和分步说明,欢迎下载。