在例如碳纤维等聚合物复合材料的制造过程中，一个关键的阶段是聚合物树脂与纤维状多孔（可渗透的）增强材料的渗透。传统上，渗透率是通过实验来测量的，但这种方法既昂贵又耗时。今天这篇博客，我们将介绍如何利用 COMSOL Multiphysics^® 软件快速、准确地建立理想的增强复合材料的渗透系数模型，以成功提高产品质量。

高分子复合材料

碳纤维增强聚合物（CFRP）等高分子复合材料由于高性能和低质量而能够大幅降低燃料和能源消耗，被广泛用于航空航天、汽车和风力涡轮机行业。碳纤维增强聚合物复合材料由两种材料组合而成。

1. 主要提供抗拉强度的纤维结构增强材料，例如碳纤维
2. 帮助在纤维之间传递载荷，同时提供压缩强度聚合物树脂，例如环氧树脂

展示了碳纤维结构和电动机的BMW i3^® 插电式混合动力概念车的剖面图。图片已通过Wikimedia Commons获得许可（CC BY-SA 3.0）。

增强材料在被排列成增强织物前，例如基于要制造的组件在长度尺度上单向或编织排列，其结构通常由直径约为 10 μ m 的单根纤维形成的成千上万根纤维，即纤维束组成。

在制造过程中，聚合物复合材料通过例如树脂传递成形（RTM）等工艺形成，包括在树脂固化之前将黏性聚合物树脂渗透到多孔（可渗透的）增强材料中。在这个阶段，树脂的流动在宏观尺度（组件的长度尺度）和微观尺度（纤维的长度尺度）上发生，其中流动可以在内丝束间发生，也可以在丝束间发生。

理解增强材料的渗透率很重要，它可以帮助：

• 提高充模（渗透）阶段模拟的准确性
• 优化注射压力等工艺参数
• 通过减少缺陷（例如未渗透区域、干点、纤维移位、丝束内和丝束间空隙形成以及称为竞流 的不均匀过滤），来提高最终产品质量

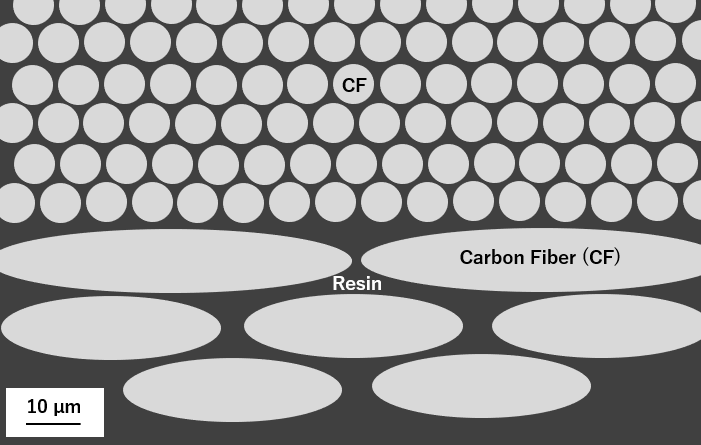
横截面图像显示了碳纤维在树脂中的典型结构、分布和尺寸。

清洁水和达西的贡献

1856 年，水力工程师亨利·达西 (Henry Darcy)在致力于改善法国第戎市（Dijon）的水质时，出版了The Public Fountains of the City of Dijon。在这部著作中，他描述了一个描述牛顿流体在宏观上通过均匀多孔介质的饱和层流的方程。这个方程就是达西定律，被广泛用于水文学应用中，并被用于模拟 RTM 工艺的模具填充阶段。达西定律的定义如下：

其中， 是表面速度（在宏观尺度上观察）， 是动态黏度， 是织物的渗透率， 是压力（尖括号表示体积平均）。

渗透率  是以面积为单位的张量，表示流体流过多孔介质的难易程度。

模拟复合增强材料的渗透率

让我们以一个理想的单向复合增强材料为例，通过将纤维束表示为排列在正方形周期阵列中的实心（不可渗透的）圆柱体来模拟横向无量纲渗透率。这种方法允许我们通过与已发表的解析解和实验结果进行比较来验证COMSOL Multiphysics的仿真结果。

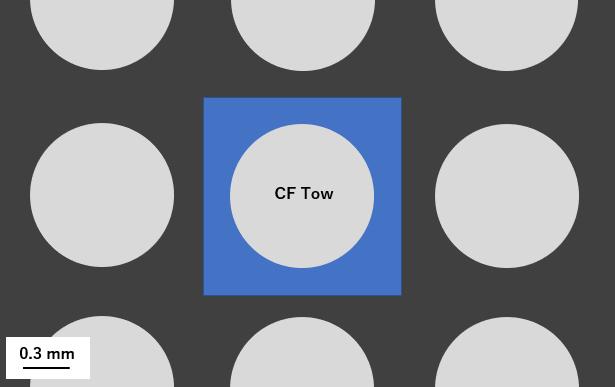
横截面图显示了理想的复合增强材料，碳纤维丝束呈方形周期性阵列，蓝色域代表基本单元。

理论

我们可以通过求解围绕圆柱体的基本单元（上图中的蓝色区域）中 纳维-斯托克斯方程的稳态解，获得圆柱体横截面的方形周期性阵列横向流动的解。但是应该注意的是，对于非常低的雷诺数流，，我们还可以在 COMSOL Multiphysics 中通过求解斯托克斯或蠕动流方程来获得解。

模型概述

基本单元模型的设置和边界条件的施加。使用周期性流动 条件和压力点约束，从左侧边界到右侧边界施加一个单位压降。然后在顶部和底部边界施加对称 条件，在圆柱体的边界施加无滑移壁 条件。用一个单位值定义流体的密度  和动态黏度  。

由于我们要计算圆柱体面积分数 从 0.05 到 0.7 的无量纲渗透率，因此可以对几何形状进行参数化，并在一次计算中对所有值进行参数化扫描。网格设置为物理场控制的极细单元尺寸，因此当圆柱体面积分数很高并且圆柱体几乎彼此接触时，我们可以用极细的网格求解相邻圆柱体之间的高速度梯度问题。

渗透率相对于圆柱半径的长度尺度无量纲化，然后通过包括阻力系数的倒数 的公式计算：

其中，  是压降和垂直于压降方向横截面积的乘积。

结果

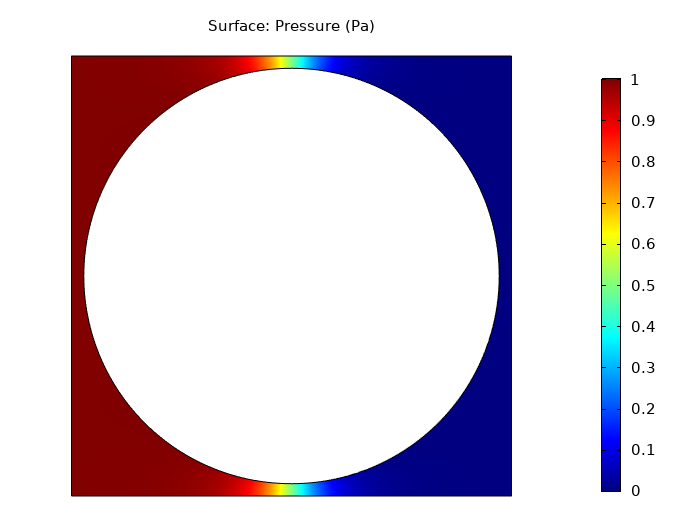
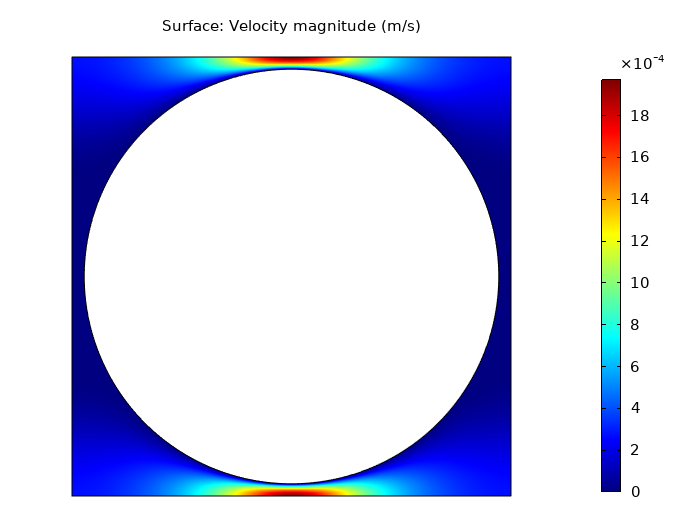
仿真结果如下图所示。压力和速度梯度在邻近圆柱体的区域中最高，流体流动间隙最小。

仿真结果显示了方形周期性圆柱阵列，实心面积的分数 时的流动压力等值线（左）和速度等值线（右） .

将无量纲渗透率的结果  与基于实心圆柱体的已发表的理论解析解和实验值进行比较，结果显示出实心面积分数 在较宽的范围内具有极好的一致性，结果显示随着 的增加，渗透率呈非线性下降。

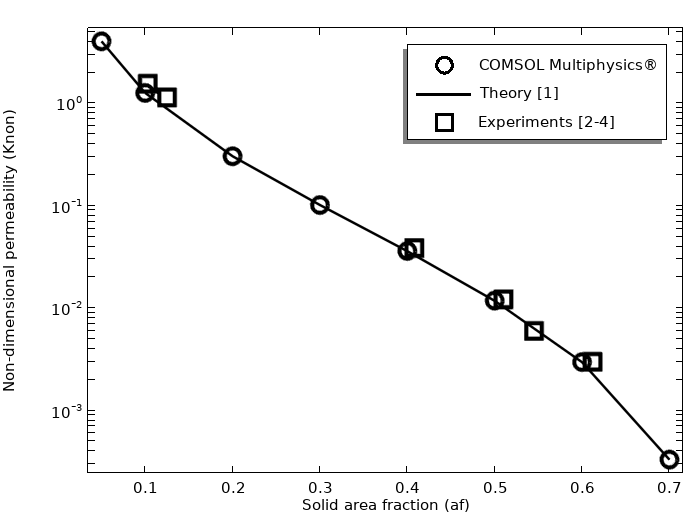
仿真结果显示了无量纲渗透率与方形周期性圆柱体横截面阵列流动的理论和实验结果比较。

结束语

在这篇博客中，我们介绍了如何使用 COMSOL Multiphysics 快速、准确地模拟理想化复合增强材料的渗透率，并通过与已发表的理论解析解和实验值进行比较来验证仿真结果，最终结果显示出模拟值与二者具有极好的一致性。该模型为平行流和更复杂的丝束形状（包括丝束内渗透率）的渗透率分析奠定了基础，为复合材料的制造和优化开发提供了更准确的模拟。

除了模拟复合增强材料的渗透率之外，COMSOL Multiphysics 还可用于模拟预测其他各种多孔材料的渗透率。

下一步

• 尝试自己动模拟文中的教程案例
  • 微型多孔结构的渗透率计算

• 阅读相关博客
  • 我应该使用哪个多孔介质和地下流动接口？
  • 使用子模型计算多孔介质中的孔隙率和渗透率
  • 复合材料模块简介

参考文献

1. A.S. Sangani, and A. Acrivos, “Slow flow past periodic arrays of cylinders with application to heat transfer”, International Journal of Multiphase Flow, vol. 8, no. 3, pp. 193–206, 1982.
2. L. Skartsis, B. Khomami, and J.L. Kardos, “Resin flow through fiber beds during composite manufacturing processes. Part II: Numerical and experimental studies of Newtonian flow through ideal and actual fiber beds”, Polymer Engineering and Science, vol. 32, no. 4, pp. 231–239, 1992.
3. T.A.K. Sadiq, S.G. Advani, and R.S. Parnas, “Experimental investigation of transverse flow through aligned cylinders”, International Journal of Multiphase Flow, vol. 21, no. 5, pp. 755–774, 1995.
4. A.A. Kirsch and N.A. Fuchs, “Studies on fibrous aerosol filters-II. Pressure drops in systems of parallel cylinders”, Annals of Occupational Hygiene, vol. 10, pp. 22–30, 1967.
5. S. McCallum, “Experimental, Analytical and Computational Studies in Resin Transfer Moulding”, in Department of Materials. 2003 Thesis (PhD), Imperial College of Science Technology and Medicine, London, UK.

BMW i3 是 Bayerische Motoren Werke Aktiengesellschaft 的注册商标。

今天，特邀博主雷庆华博士和我们一起讨论了一种新的模拟裂隙介质中全耦合流体力学过程的方法。

了解裂隙地质介质中固体变形与流体流动之间的耦合关系，对于解决地球科学和岩土工程中的许多核心问题，例如地下挖掘、油气开采、碳封存、地热生产和废物处理，具有重要的意义。本文描述了一种基于 COMSOL Multiphysics® 软件的裂隙介质中全耦合流体力学过程建模的新方法。

为什么使用 COMSOL Multiphysics^® 进行流体力学建模?

一般来说，模拟裂隙介质中的耦合流体力学过程存在两个主要挑战。一个是内含大量的天然裂隙的地质介质的不连续性表征，这些裂隙普遍存在许多不同的长度尺度，并经常主导系统的整体行为（参考文献 2）。另一个是流体力学耦合机制的计算，包括直接耦合（即固体和流体场之间的相互作用）和间接耦合（即岩石/裂隙性质的改变）。

在过去的几年中，已经开发了大量旨在应对这些挑战的商业软件包和开源研究代码。然而，其中大多数必须使用不同的求解器来计算流体和固体方程，因此必须通过额外的处理步骤来实现耦合，这既不方便也不高效。此外，大多数现有代码无法真正同时捕获直接和间接耦合，因此通常必须进行假设或简化。

使用 COMSOL Multiphysics 是因为它具有卓越的功能:

1. 同时求解多物理场方程，实现直接耦合
2. 将模型参数定义为其他场变量的函数，实现间接耦合
3. 明确表示离散的裂隙，并求解其中的物理过程(如裂隙流动和裂隙变形)

下面，我们将阐述在 COMSOL Multiphysics 中建立裂隙介质全耦合流体力学数值模型的步骤，并给出一些仿真实例。

建模过程

在 COMSOL Multiphysics 中进行数值仿真涉及三个主要步骤。

步骤1:生成模型几何和网格

首先，可以使用 AutoCAD® 或 Rhinoceros® 等 CAD 软件构建几何上表示为线/折线的离散裂隙网络。然后将几何数据导出为 DXF 文件，这些文件可以直接导入 COMSOL Multiphysics。这一步骤也可以在 MATLAB® 中完成，以按照规定的概率分布生成合成裂隙网络，并将其导出到 DXF。

提示：您还可以使用离散裂隙网络插件直接在 COMSOL Multiphysics 内部的现有几何结构中创建随机裂隙，如裂缝性储层的 3D 示例模型所述。

导入几何图形后，我们使用三角形有限元的非结构化网格（通过 Delaunay 细分）对域进行离散化，其中天然裂隙由嵌入相邻有限元之间的联合单元表示（图1）。

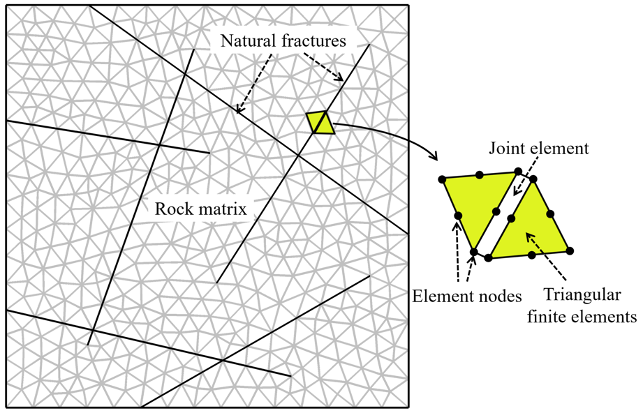
图1。该模型采用三角形有限元的非结构化网格离散化，其中天然裂隙由嵌入相邻有限元之间的联合单元表示。

第二步:模型设置并定义材料属性、耦合参数和边界条件

我们使用 COMSOL Multiphysics 中的固体力学 和达西定律 接口对裂隙介质中的流体力学过程进行了模拟。我们激活 多孔弹性 接口以实现固体和流体方程之间的直接耦合。我们定义了岩石基质和裂隙的材料特性和本构方程。一些岩石/裂隙特性，例如孔隙率、储水和渗透率，被定义为局部应力/压力状态的函数，以实现间接耦合。我们还定义了力学和水力边界条件。

第三步:解的计算

我们在两个连续的阶段运行模型。在第一阶段，系统在给定的原位 应力和压力条件下达到初始平衡（通过斜坡加载）。然后，在第二阶段，我们模拟系统对流体注入或地下开挖等工程活动的响应。

仿真实例

示例1:裂隙岩石中的流体注入

我们应用该模型来模拟受流体注入影响的裂隙岩石的流体力学行为（参考文献 1）。该模型可以真实地捕捉裂隙多孔介质中的压力扩散，完整岩石中由脆性和疲劳引起的损伤以及裂隙结构对流体力学过程的重要影响（图2）。该模型还使我们能够直观地查看裂隙岩石中损伤、应力和压力场的详细演变，并进一步研究多孔弹性对驱动系统中新损伤传播的基本控制（图 3）。根据模拟结果，我们还可以分析由完整岩石脆性破坏和/或天然裂隙摩擦滑动引起的诱发地震活动的时空演变（图4）。

图2 注液过程中裂隙岩石的压力演化与损伤扩展。

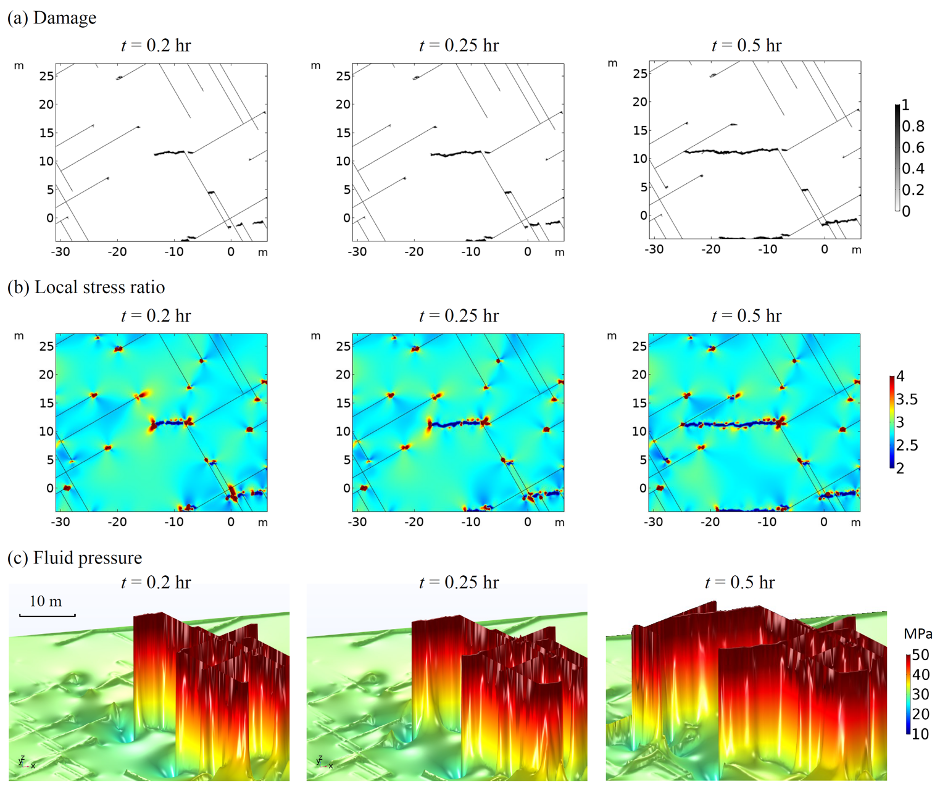
图3 查看(a)损伤的分布情况;(b)应力比(即局部最大主应力与局部最小主应力的比值);(c)裂隙岩石局部区域的流体压力(通过高度表达式显示)。

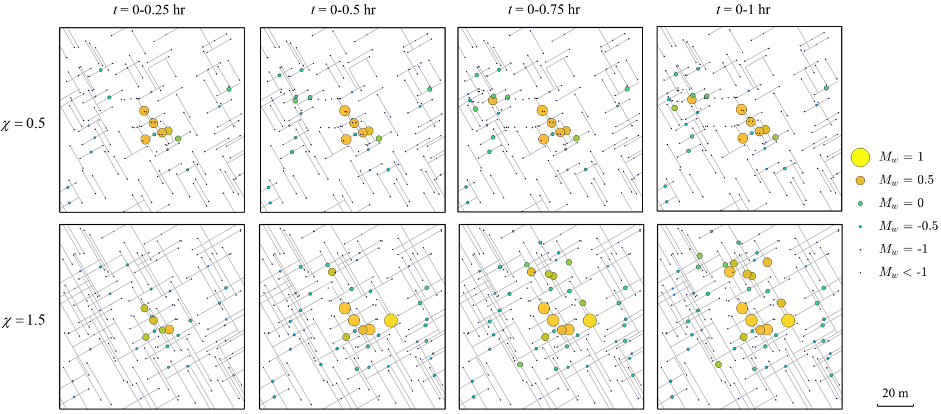
图4 低、高裂隙密度分别为χ = 0.5 和 1.5 的裂隙岩石中诱发地震事件的空间分布和演化规律。

示例2:裂隙岩石的地下开挖

该模型也可用于模拟裂隙岩石中开挖引起的扰动以及由此产生的瞬态流体力学行为（参考文献4）。我们捕获了由于挖掘（时间 t = 0-0.1 小时）和随后的排水（时间 t= 0.1~20 h) 过程导致的显著的压力变化和扩散以及应力变化和损伤演变（图5）。我们通过对 Biot 系数进行敏感性分析来说明流体力学耦合的重要作用。结果表明，当Biot系数越高(或者说耦合越强)时，开挖引起的孔隙弹性压力场越不均匀，岩石损伤和破裂位移也越大。开挖和排水过程都会诱发与岩石基质的脆性损坏和/或天然裂隙的摩擦滑动相关的地震事件（图 6）。

图5 裂隙岩石在开挖过程中及开挖后的压力、应力和损伤演化。

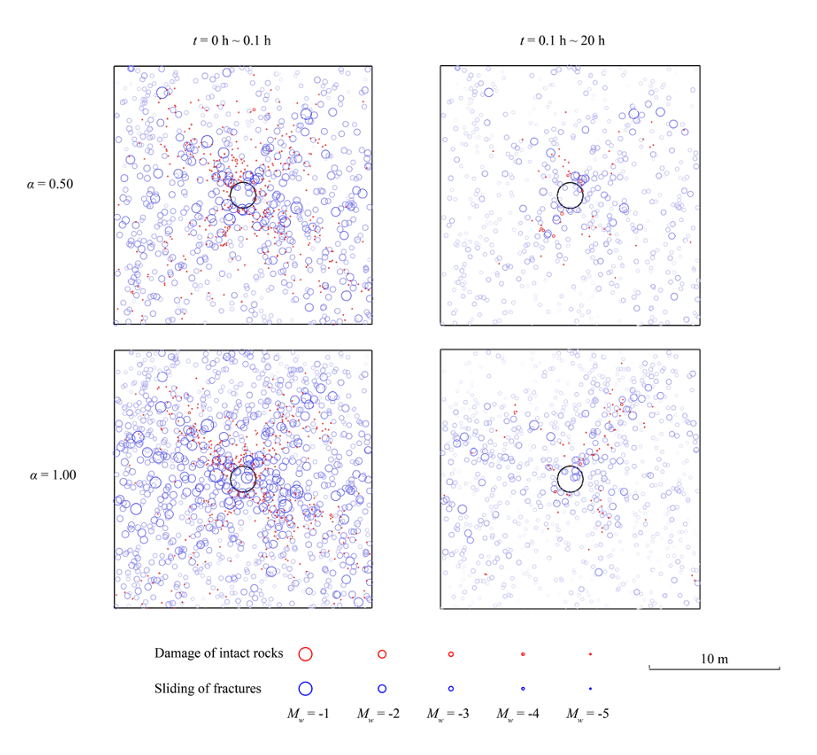
图6 在开挖(左图)和排水(右图)阶段，具有不同 Biot 系数 α 的裂隙岩石的地震活动的空间分布。

除了上述的流体力学模型外，我们还开发了一个完全耦合的热流体力学模型来模拟裂隙性地热储层在长期水循环和产热过程中的性能(参考文献3)。

参考文献

1. Q. Lei et al., “Modelling fluid injection-induced fracture activation, damage growth, seismicity occurrence and connectivity change in naturally fractured rocks”, International Journal of Rock Mechanics and Mining Sciences, no. 138, vol. 104598, 2021.
2. Q. Lei et al., “The use of discrete fracture networks for modelling coupled geomechanical and hydrological behaviour of fractured rocks”, Computers and Geotechnics, no. 85, pp. 151–176, 2017.
3. Z. Sun et al., “Combined effects of thermal perturbation and in-situ stress on heat transfer in fractured geothermal reservoirs”, Rock Mechanics and Rock Engineering, no. 54, pp. 2165–2181, 2021.
4. C. Zhao et al., “Role of hydro-mechanical coupling in excavation-induced damage propagation, fracture deformation and microseismicity evolution in naturally fractured rocks”, Engineering Geology, no. 289, vol. 106169, 2021.

关于作者

雷庆华博士，讲师，瑞士 ETH Zürich 地球科学系高级科学家。他拥有中国同济大学土木工程学士学位(2009 年)和硕士学位(2012 年)，以及英国帝国理工学院岩石力学博士学位(2016 年)。雷博士是国际岩石力学和岩石工程学会(ISRM)的 Rocha 奖章，以及 NGW Cook 博士论文奖和美国岩石力学协会(ARMA)的岩石力学研究奖的获得者。雷博士的研究兴趣包括岩石力学、耦合过程、断裂表征、多相流、地震波、诱发地震活动和边坡稳定性。他是断裂岩石热-水力-机械-化学过程 ISRM 委员会的秘书长，ARMA 未来领导人，以及 ARMA 地下储存和利用技术委员会的创始成员。

Autodesk、Autodesk 徽标、AutoCAD 和 DXF 是 Autodesk, Inc.和/或其附属公司和/或关联公司在美国和/或其他国家的注册商标或商标。

Rhinoceros 是 TLM, Inc. 的注册商标。DBA Robert McNeel & Associates Corporation。

MATLAB 是 The MathWorks, Inc. 的注册商标。

在上一篇博文中，我们介绍了基于侧流分析（LFA）的快速检测的原理。今天这篇文章，我们来看看如何利用这种测试检测新冠肺炎（COVID-19）。另外，我们使用 COMSOL Multiphysics^® 模拟了三个模型，用于理解这些简单的、稳固的和先进的微实验室是如何工作的。

新冠肺炎是如何检测的？

当人体感染新型冠状病毒 SARS-CoV-2 后，免疫系统会迅速形成抗体。树突状细胞可能呈现病毒抗原，以便被 T 细胞识别。T 细胞可以激活 B 细胞，分泌靶向抗原的抗体(参考文献1)。首先形成的是 IgM 抗体。这些抗体一旦靠近就会附着在病毒颗粒的抗原表面。例如，就冠状病毒而言，这些抗原可以是病毒表面的刺突蛋白(S 抗原)。一旦附着在抗原上，抗体就会阻断病毒的刺突蛋白，阻止它们附着并感染人类细胞。这样就可以中和病毒，因为它不能在受感染的细胞外复制。有许多不同的抗体可以靶向不同的抗原。需要注意的是，人体还有其他对抗感染的机制。此外，识别病毒的T细胞也可能直靶向受感染的细胞。它们可以指示细胞进行自我毁灭，或者杀死被感染的细胞，从而中和病毒。

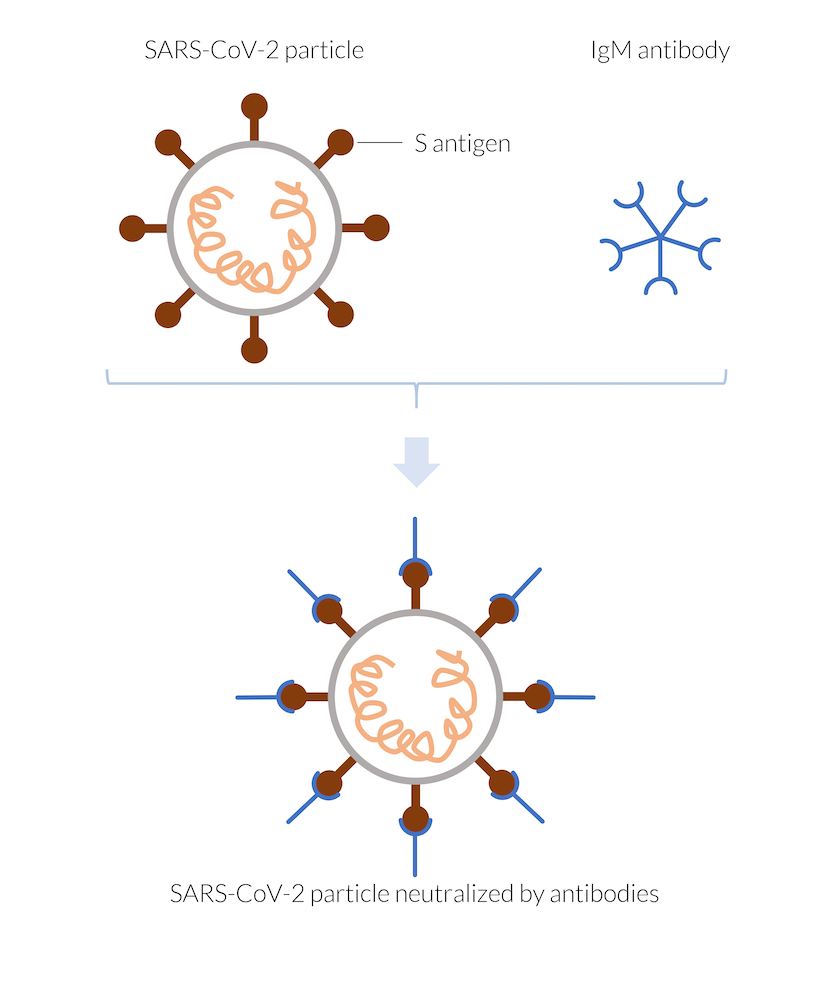
由免疫系统制造的 IgM 抗体附着在例如新型冠状病毒颗粒的刺突抗原(S 抗原)上，从而中和病毒颗粒。被中和的病毒颗粒不能进入人体细胞，因此不能进行自我复制，最终被破坏。

IgM 抗体五个一组形成小颗粒(或大分子)在人体内巡视，附着在他们遇到的每一个病毒颗粒上。在感染的后期，免疫系统还会形成其他抗体，例如 IgG，它们会自动巡视身体，并附着在能看到的每一个病毒颗粒上。IgG 抗体需要更长的时间才能被身体制造出来，但是它们持续时间也更长，并且只要存在 IgG 抗体就可以产生免疫力。

新冠肺炎的一些LFA快速检测是基于 IgM 和IgG 抗体的检测。这些就是本篇博文建立的模型所研究的测试。

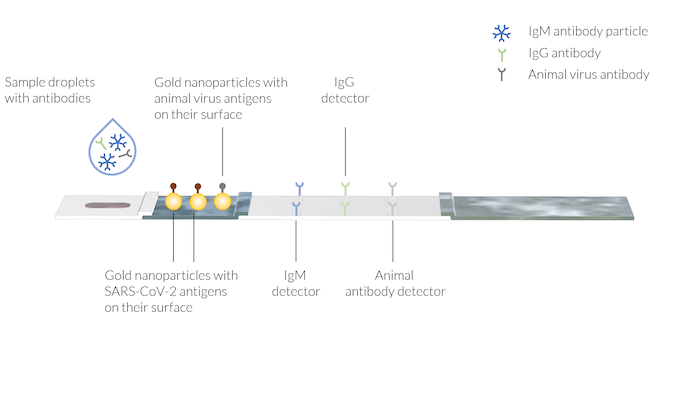
样本中含有因感染新冠肺炎而产生的人类抗体 IgM 和 IgG。动物抗体也与缓冲溶液一起被加入样本液体中。在三个不同区域的测试线上固定了抗体检测试剂。请注意，图中测试线尚不可见。

在检测时，可以将患者的血液(或唾液)施加到样品孔上，然后在样品孔中滴入几滴缓冲液，来应用缓冲液。

样品在毛细管力的作用下被输送到连接板上。在这里，IgM 和 IgG 抗体与标记物形成络合物。络合标记物可能是一个表面上具有新型冠状病毒抗原的纳米金颗粒。之后形成两种不同的络合物:

1. IgM 的络合物（IgM-C）
2. IgG 的络合物（IgG-C）

这些络合物在样品溶液中溶解。

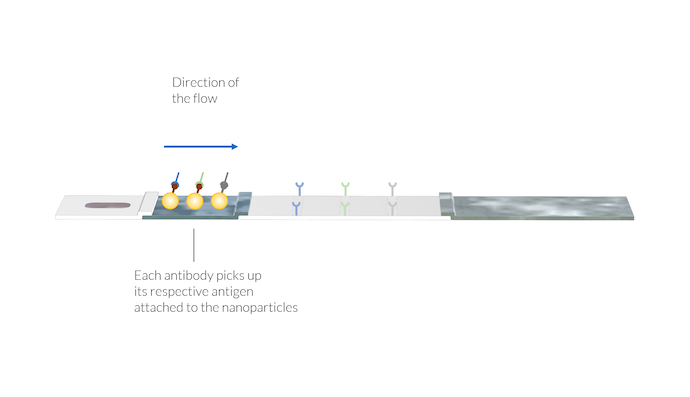
IgM 和 IgG 抗体通过附着在颗粒表面的 SARS-CoV-2 抗原被吸附到纳米金颗粒（络合物标记）上。此外，动物病毒抗体会吸附各自的纳米金颗粒。抗体和颗粒的络合物溶解在流动液中，并与样品溶液一起被运送到膜上。请注意，此时测试线仍不可见。

此外，可能还有第二个与来自动物病毒的抗原结合的纳米金颗粒。这些络合标记物可以附着到缓冲溶液提供的参考动物抗体上。动物抗体和络合标记物(AA-C)的络合物也溶解在样品液体中，并用于随后的对照线检测。

样品随后在毛细管作用力下被输送到膜上。在第一条测试线中， IgM 检测试剂在膜的制造过程中被固定在膜表面。这些 IgM 检测试剂会捕获 IgM-C 络合物，并使这些络合物固定在该测试线的区。纳米金颗粒发生聚集并将测试线染成红色，显示测试线上络合物的存在。

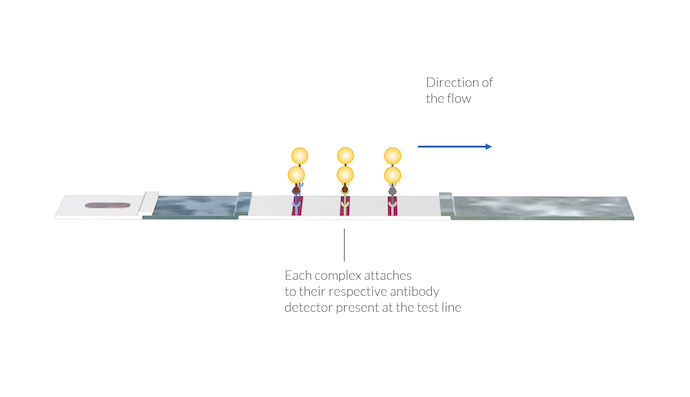
抗体-抗原-纳米金颗粒络合物附着在各自的抗体检测试剂上，抗体检测试剂位于测试线的位置。一旦络合物被固定在测试线表面，由于表面上存在纳米金颗粒，测试线颜色就会出现。

同样，在第二条测试线上，IgG-C 络合物与固定的IgG检测试剂发生反应。一旦 IgG-C 络合物附着到 IgG 检测试剂上，由于纳米金颗粒的存在，第二条测试线的颜色会变为红色。

然后，当对照测试线遇到氨基酸-碳络合物（AA-C complex）时，通过附着在对照测试线区域膜上的动物抗体检测试剂，以类似的方式进行反应。对照测试线的颜色显示样本已经通过膜区，包括IgM和IgG检测区。如果对照测试线没有着色，那么该测试应该被视为无效，因为样本没有以预期的方式通过膜。

液体溶液继续流向吸收板(芯板)。吸收板的孔体积决定了可以流过测试条的样品体积。一旦吸收路径满了，测试条中的液体流动就停止了。重新开始流动的唯一可能是蒸发吸收板中的一些样品液。

使用 COMSOL Multiphysics^® 建立的快速检测的3种模型

本文作者使用 COMSOL 建立了 3 个模型用于研究 LFA 快速检测。

首先，使用一个完整的 3D 模型，以确定样品液体是否均匀分布在测试条中，并研究采样孔位置的影响。此外，可以使用 3D 模型研究吸收板的吸收能力，以得到穿过测试条的流量。

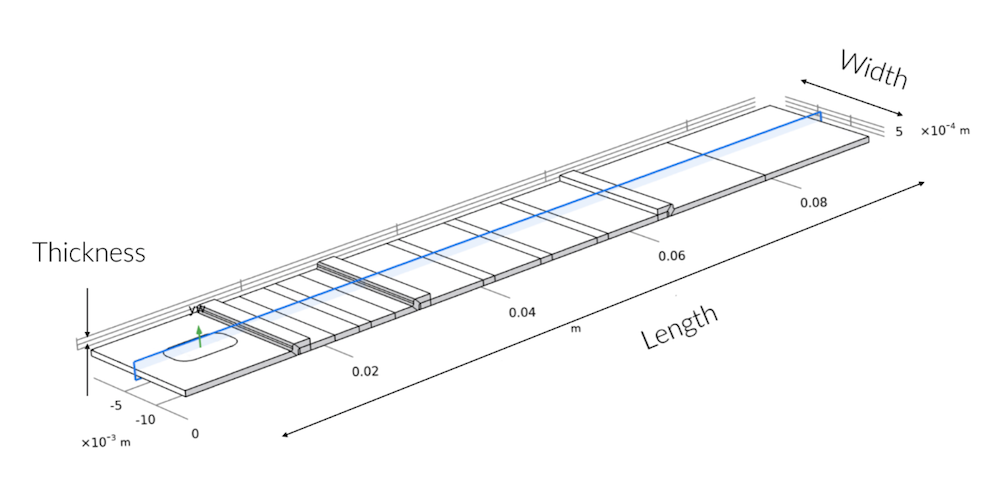
蓝色阴影横截面显示了 3D 几何图形中的 2D 建模平面。沿宽度方向的对称偏差仅出现在样品板中，其中，样品板中的样品孔没有布满测试条的整个宽度。

很快我们发现，一旦样品溶液通过样品板，样品液流动会迅速形成一个平坦的速度曲线。这意味着它沿着测试条的宽度均匀流动，也就意味着 2D 模型足以理解快速检测装置的挑战和功能，只要样品板能够均匀地分配流体。因此，我们使用 2D 模型来研究测试条中的传输和反应。2D 模型允许我们沿着测试条的长度和厚度使用更高分辨率的网格。

这些模型结合使用了 COMSOL Multiphysics 中用于多孔介质流动的理查兹方程 接口和稀物质传递 接口(参考文献2)。形成 IgM-C、IgG-C 和抗 AA-C 络合物的反应由 化学 接口定义。此外，测试线上的表面反应也由化学 接口定义。对于 2D 模型，我们使用了两种不同的方法:

1. 假设络合物在测试线上的吸附仅发生在膜表面
2. 假设检测中的吸附过程发生在测试线位置下方的整个膜厚度上

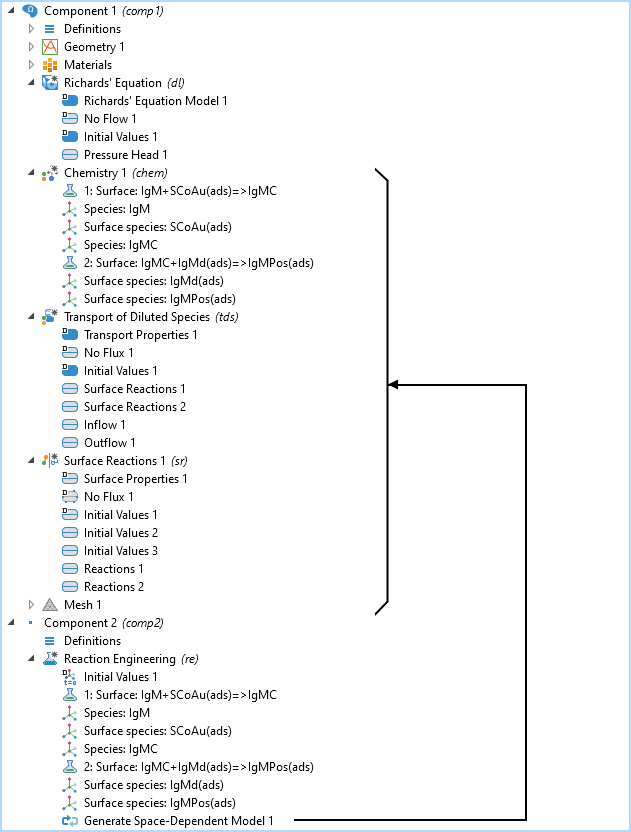
含 2D 模型组件和 理查德方程模型的模型树，化学、稀物质传递，表面反应接口，和 反应工程接口。生成空间相关模型节点将传输和化学接口添加到已经存在的 2D 模型组件的理查德方程接口。

IgM 反应路径的模型树如上图所示。化学，稀物质传递 和表面反应 接口都均是由反应工程 接口建立的，其中使用了生成空间相关模型 功能。

连接板中的化学反应定义如下:

1. 连接板中纳米金颗粒上的 IgM 和 SARS Co-2 抗原之间的反应定义为:

IgM +SCoAu(ads) => IgMC

1. • 术语(ads)用于表示抗原和纳米粒子被吸附在连接板的孔结构中，并被 IgM 吸附以形成 IgMC 络合物，IgMC 络合物溶解在溶液中。
2. 可以得到IgG抗体的类似反应: IgG + SCoAu(ads) => IgGC
3. 动物抗体与动物抗原在纳米金颗粒上的反应可定义为: AA + AAu(ads) => AAC

因此，IgMC、IgC 和 AAC 是共轭抗体络合物。

测试线中的反应如下:

1. 在第一条测试线上: IgMC + IgMd(ads) => IgMPos(ads)
   • 上式说明了IgMC络合物与吸附的IgMd检测蛋白反应，形成吸附的IgMPos表面络合物。IgMPo络合物可以使第一条测试线变色。
2. 类似于上面的4条，在第二个测试线中，有: IgGC + IgGd(ads) => IgGPos(ads)
   • 吸附的 IgPos 络合物使第二条测试线呈现红色。
3. 在第三个测试线中，有: AAC + AAd(ads) => AAPos(ads)
   • 吸附的物质 AAPos 使参考测试线呈现红色。

模型结果

下图显示了测试条在四个不同时间的流动曲线。我们可以看到，最初，样本前端沿着测试条的中部进一步延伸到测试条中，形成一个略微呈抛物线的曲线。抛物线曲线是由于样品孔处于测试条的中间位置。然而，5 秒钟后，当样品溶液流动已经达到连接板的三分之一时，流动曲线是平坦的(见上一篇博文中的最后一个图)。

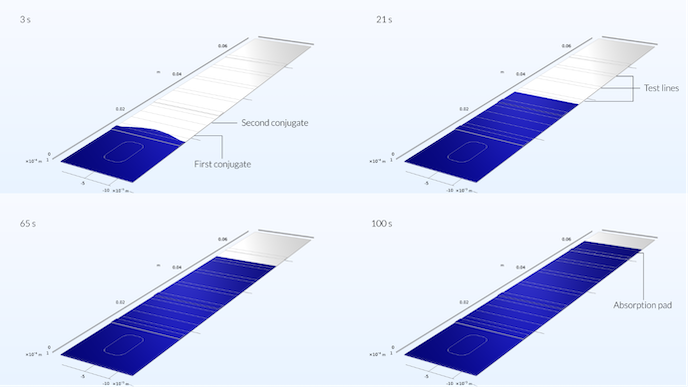
样本在 3 秒钟后已经到达第一个结合区域。在这里，我们仍然可以注意到样品孔的位置对样品液延伸的影响，因为它不是平坦的，而是在中间显示出最大的延伸。21 秒后，当样本液到达第一个测试线区域时，速度曲线是一条直线。65 秒后，样本液流到达参考测试线，100 秒后到达吸收板。

由上图我们还可以看到，样品液沿着垂直于通道中间测试条的平面是对称的。这意味着我们只需要求解一半的装置就可以解决这个问题。尽管这是一个对称问题，但对整个装置进行建模是一个很好的方法，可以检查网格是否足够密集，以得出关于流动曲线的任何结论。流动曲线是对称的表明这里的网格可能足够密集。

下面，我们来看看第一条测试线位置处样品的流速图，见下图。我们可以看到，在样品被施加到样品孔后大约 20 秒开始流动，流动在 275 秒左右停止。这与吸收板充满液体样品的时间一致。

同样有趣的是，流速随着时间的推移几乎呈指数衰减。这是因为驱动流动的毛细管力仅作用在样品溶液与空气相遇的孔隙表面(液体前沿的三相边界区域)。这意味着毛细管力是恒定的，只要有自由孔隙体积，都可以用样品溶液填充。然而，随着样品溶液体进一步进入测试条，流动阻力增加。与流动样品液体接触的孔壁面积随时间增加，因此孔壁和流动溶液之间的摩擦面积也会增加。

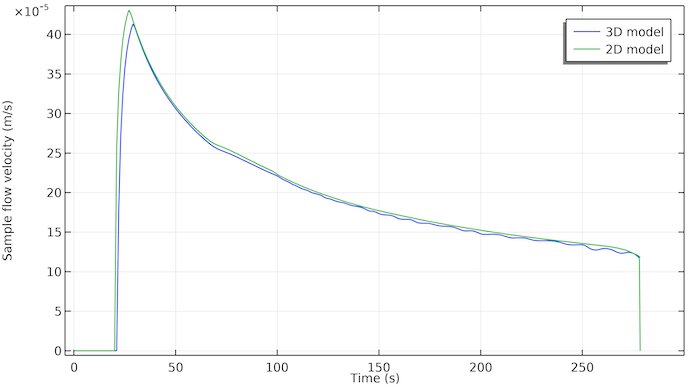
3D 模型(蓝色)和 2D 模型(绿色)第一条测试线位置处的样品流速。这两条曲线非常吻合。3D 模型显示大约 2 秒钟的延迟，这可能是因为样品最初必须沿着宽度流动。在 2D 模型中，样品立即沿宽度均匀分布。

下图显示了不同时步下 IgMC 络合物的浓度。我们可以看到，IgMC 络合物随着流体流动，直到到达第一条测试线的区域。在这里，它与 IgM 检测物质反应后被消耗，形成有色检测线。IgMC 浓度场显示，样品溶液到达测试线后，形成浓度边界层。随着时间的推移，测试线后的浓度耗尽流体继续流动，但测试线周围区域几乎达到稳定状态。然而，一旦流动停止，当吸收板被样品液充满饱和时，则在测试线以下形成更厚的遍及整个膜的耗尽区。以类似的方式，连接线下方的区域也被 IgMC 络合物充满。

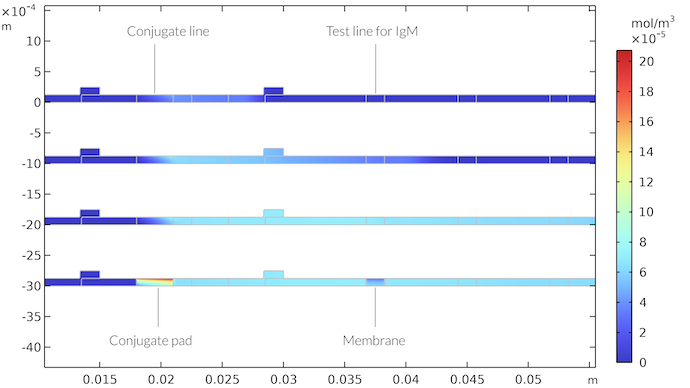
连接板和膜中IgMC的浓度场是时间的函数。时间分别为 21 秒(上)、65 秒、260 秒和 410 秒(下)之后。410 秒后，测试条中不再有任何流体。我们在连接板中得到一个高 IgMC 浓度的区域，在 IgM 测试线以下得到一个低 IgMC 浓度的区域。

如果在测试线的表面绘制检测物质的粒子浓度图，流量的影响是明显的。当流量到达相应的测试线时，粒子浓度开始增加。随着 IgMC 被吸附在测试线区域并形成检测 IgMPos 物质，浓度几乎是线性增长的。线性增长意味着恒定的吸附速率。当流动停止时，由于吸收板饱和，IgMPos 继续以大致相同的速率形成。这意味着，在这种情况下，IgMPos 的形成由吸附动力学决定，即由 IgMC 中的纳米金粒子对吸附位点的吸附速率决定。如果它是由质量运输控制的，我们会看到曲线斜率的变化，当流动停止时，增长会减慢。如果改变吸附动力学的速率常数，曲线斜率当然也会改变。测试线的可见度大约从每平方毫米 1·10⁸ 个粒子开始。

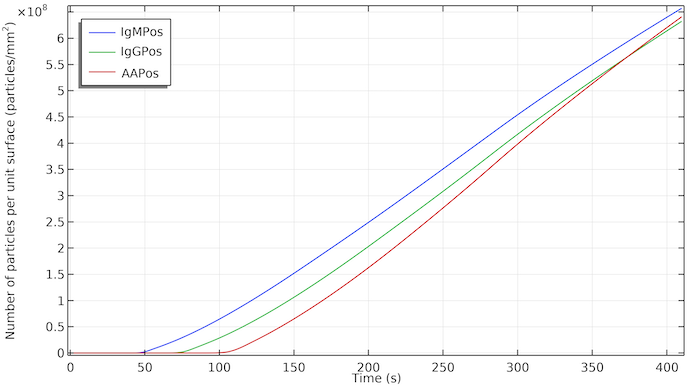
在各自的测试线表面的 IgMPos, IgGPos,和 AAPos 浓度是时间的函数。IgMPos 和 IgGPos 竞争同一个络合物标记，因此 AAPos 生长稍快。

因此，如果三条测试线的动力学相似，我们会看到第一、第二和第三条(对照)测试线的显示延迟。此外，每条测试线将在面向流动的边缘开始着色，测试线的尾部会稍晚显示。

如果我们将动力学调整为均相流动，均相模型显示出类似的结果。然而，此时的传输要快得多，因为反应位点遍布在连接板的整个厚度，测试线则横跨膜的厚度。反应物不必被运输到测试条的表面。这是一个更复杂的过程，其中动力学和质量传输都限制了测试线的显示。下图显示了对应于上述非均相流动的 IgMC 浓度。

当共轭区包含整个厚度的共轭标记，并且测试线存在于整个膜的厚度时，IgMC 的浓度。其结果与非均相情况类似。

下图揭示了测试线的真实情况。我们可以看到，它在流动方向上有一个小的倾斜，就开始几乎均匀地显现。当流动停止时，测试线两个边缘显出的颜色饱和度更高，因为会有更多的抗体-缀合物络合物通过扩散运输到这些边缘。

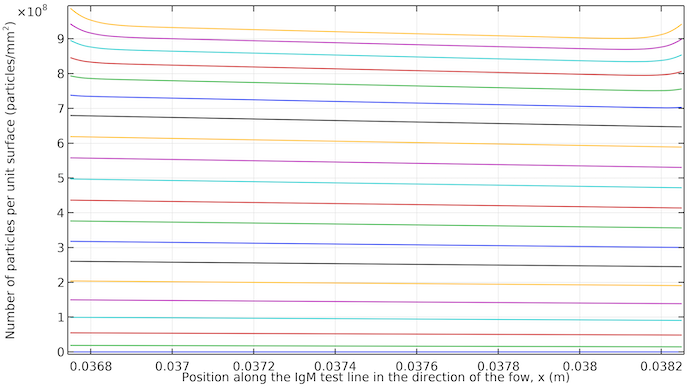
在 IgM 测试线上，每单位表面积的 IgM 络合物浓度厚度超过 10μm。曲线从 20 秒到 400s，增量为 20s。曲线从底部的 20s(低饱和度)开始，到顶部的 400s(高饱和度)结束。大约 260s 后，时步之间的曲线更接近，因为扩散是将抗体-络合物标记络合物运输到测试线区域的唯一方式，从而减慢了过程。

真实的情况可能介于同质和异质模型之间。我们可以认为，获得沿其宽度均匀着色的测试线的好方法是使检测体积接近测试条的表面。这样，传输可以在 x 和 y 方向发生，同时我们得到一个相对较大的反应区(见下图)。对于测试线来说，将反应区扩展到膜的整个厚度对测试并没有帮助，因为膜是不透明的。然而，将连接板的反应区分布在整个厚度上是有利的，因为这将使络合物标记和抗体之间的反应最大化。这样，络合物标记将尽可能多地吸附抗体。

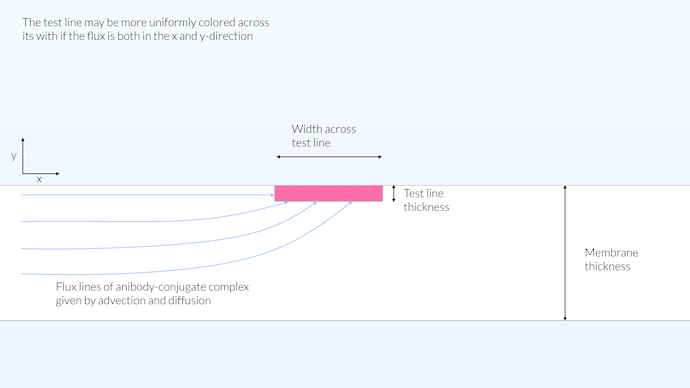
在这种配置中，测试线的反应区不限于表面，也没有分布在膜的整个厚度，其厚度被限制在 15μm。膜不透明，并且几乎不透明，可见深度约为 10μm。有限的测试线厚度允许在测试线的整个宽度上传输，从而在膜的整个宽度上产生相对均匀的颜色饱和度。

结束语

样品在测试条上流动的间隔由吸收板的尺寸决定，吸收板的尺寸也决定了样品的尺寸。更有趣的是，该模型预测了样品在测试条上流动时流速的指数衰减，这对于该领域的科学家来说也是众所周知的，但可能并不完全明显。2D 模拟显示，测试条中的质量传输似乎很慢，在非均相流动情况下，速率决定了测试。流动似乎可以快速地将样品分布在测试条上。然而，吸附反应是如此缓慢，以至于在非均相情况下，质量传递仍然限制了抗体-抗原-纳米粒子复合物向测试线处的吸附表面扩散。在均相流动的情况下，吸附动力学的限制更大。然而，这当然与我们使用的输入数据有关。

为这篇博文中建立的模型仅是一个化学原理。如果要将它们用于测试条的实际开发，必须在获得化学和多孔材料的特性的输入数据上做更多的努力。然而，这些模型包含了重要的物理现象:相对详细的传输和反应描述。

模型改进的可能性：

• 考虑沿膜各处的吸附-解吸。文中我们假设所有物种自由传输，直到它们在测试线上被永久吸附。
• 建立更精确的两相流模型。我们使用了一个简单的多孔介质两相流模型。也可以使用基于相位场的更精确的模型。
• 使用科学文献中公布的特定测试的输入数据。我们对测试条组件中的所有板使用了相同的孔隙率和润湿特性。浓度和吸附动力学使用了产生合理结果的输入数据。然而，为了使用真实的浓度和动力学数据，应该进行文献检索。然而，这对于不同的新冠肺炎检测是不同的，因为每个制造商都有自己的样品制备和检测程序。这篇博文的目的仅仅是展示可能的建模方法，而不是发表科学论文。
• 网格收敛分析。这将显示您在模拟结果中可以预期的准确性。这已经部分完成，我们知道模型给出的数值误差相对较小。但是如果需要严格的精度，就不属于这篇博文的讨论范围了。

参考文献

1. L. Gutierrez, J. Beckford, and H. Alachkar, “Deciphering the TCR Repertoire to Solve the COVID-19 Mystery”, Trends in Pharmacological Sciences, vol. 41, no. 8, pp. 518–530, 2020, (https://www.cell.com/trends/pharmacological-sciences/fulltext/S0165-6147(20)30130-9),
2. D. Rath and B. Toley, “Modelling-Guided Design of Paper Microfluidic Networks – A Case Study of Sequential Fluid Delivery”, ChemRxiv, 2020, https://doi.org/10.26434/chemrxiv.12696545.v1.

下载模型

您是不是也想尝试模拟对 COVID-19 的快速检测？单击下面的按钮访问案例模型文件，自己动手模拟:

新冠肺炎的大流行让全世界的人们意识到追踪接触者的重要性。为了能够控制病毒感染的大爆发，需要知道谁被感染，以及这个人什么时候在哪里被感染。对这种知识的缺乏迫使世界上大多数国家实施了限制和封锁措施，这导致了严重的社会混乱和全球经济衰退。

快速检测测试设备的成功研发使人们能够在关键的、并且无法封闭的社会领域进行接触追踪，例如医疗保健和食品供应行业。价格低廉的测试方法也使人们能够快速进行自我诊断，并在得知感染的情况下进行自我隔离。这也有助于减缓病毒的传播。韩国和德国已经成功地利用这种测试在更大范围内减缓了新冠肺炎在群体中的大流行 (参考文献1).

快速检测新冠肺炎的一种可能的测试手段是基于侧向层析测定法(LFA)，也称为侧向流免疫层析测定法(LFIA)或免疫层析试验。我们在超市就可以买到的标准验孕棒可能就是LFA最常见的一种应用。LFA 为许多疾病和病症提供了一种便宜的、相对可靠的、稳定的和易于使用的测试手段(参考文献2).

本文是系列博客（由两部分组成）的第一篇文章，下面我们将使用 COMSOL Multiphysics 软件来了解 LFA 设备的功能以及工程师在设计这些设备时可能遇到的挑战。

LFA 快速检测测试背后的原理

如果对这些快速检测测试背后的机制进行仔细研究，我们可以看到，这些测试设备是相当先进的，并且是一个非常强大的微型实验室。

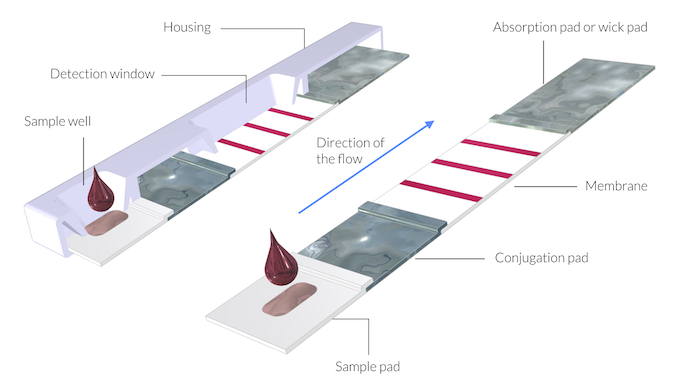
快速检测测试装置示意图。这里为了显示测试装置的结构，膜和平板的厚度被放大了 5 倍。平板和膜的组装件称为测试条。

测试条由以下几部分组成(如上图所示):

• 样本板
• 连结板
• 膜
• 吸收板，也称为吸液板

测试条通常由不同的组件(板和膜)组装而成。测试条外有一层塑料保护壳 (参考文献3)。

测试板和膜是多孔结构的。孔壁应该会被样本液润湿。样本可以在被施加到测试条上之前制备，也可以在样本板中制备。通过将血液或唾液与缓冲液混合来获取样本。缓冲液可能含有参考抗体和其他化学物质，例如能够确保样本润湿不同组分孔壁的溶剂。

样本板用于接收样本液滴，并充当流动的分配器和过滤器。非常大的蛋白质和血液细胞会被截获在样本板的多孔结构中。此外，多孔结构确保了样本液体能够沿板的宽度均匀分布。一旦样本充满了样本板，它就会继续向连结板的方向流动，流动是由液体与孔壁的相互作用引起的毛细管力驱动的。

在连结板中，过滤后的样本会溶解试剂，即所谓的“连结标签”，这些试剂在制造过程中已经被施加到连结板上。标签通常附着在例如金纳米粒子表面的抗原上。抗原可能是一种在免疫系统中能引发抗体的蛋白质。这些标签可以附着在样本中的抗体上，形成抗体和连结标签的络合物。络合物会溶解在样本液中，它们可以由附着在患者抗体上的标签和附着在制备过程中混合在样本中的参考抗体上的标签组成。一旦样本液填满了连结板中的孔，就会继续到抵达膜的位置，再次由毛细管力驱动前进。

样本液继续流过膜。膜通常由多孔硝酸纤维素制成，但也可以使用其他材料制备。不同的蛋白质和化学物质也可能与多孔膜的孔壁产生相互作用。一些物质可能在孔壁上被吸附和解吸。这种相互作用倾向于沿着流道分离不同的物质，这取决于物质分子的大小以及它们与孔表面相互作用的亲和力。这种作用被称为“免疫层析”。

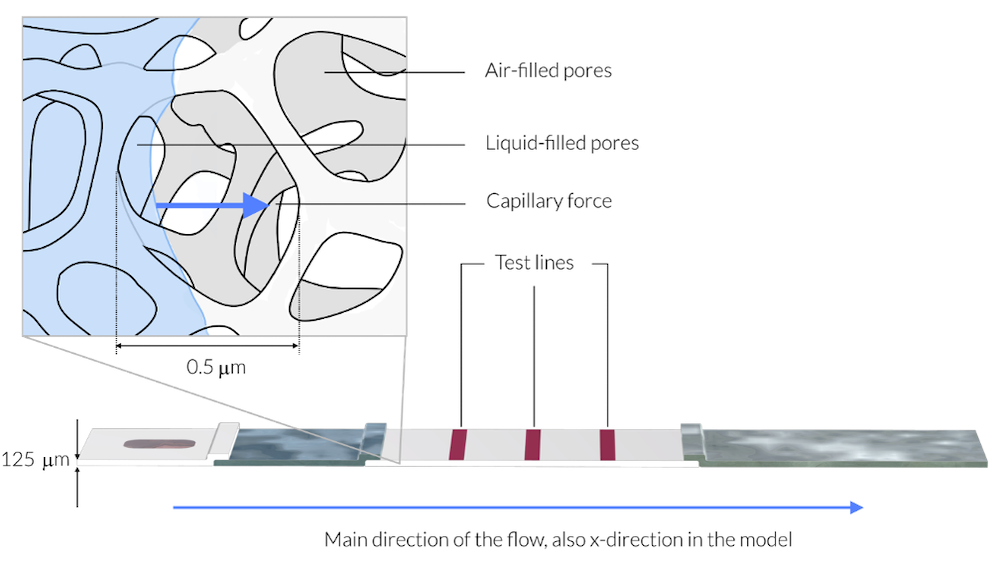
在这幅图中，样本液体刚刚到达膜的位置。放大显示为一个边长约 1µm 的矩形。平均孔径约为 0.5µm。作为比较，膜的厚度为 125µm (参考文献3)。液体样本用浅蓝色表示。膜由固态网格组成，像骨架一样，孔占膜体积的 70%。样本液体润湿骨架结构的壁，即孔壁，并在毛细管作用力的驱动下沿蓝色箭头指示的方向进入充满空气的孔中。请注意，为了清晰起见，该图中测试条的厚度被放大了 5 倍。

一旦样本与测试线接触，其中的一种络合物中就可以附着到测试线区域中存在的特定表面物质上。这种表面物质可以是固定在测试线表面的抗体。每条测试线可以连接一种特定的络合物。注意，表面物质在测试线区域是静止的；它既不溶解也不会被样品运输。一旦络合物附着到测试线上，测试线的区域就会改变颜色。颜色显示出特定抗体的特定络合物已经附着到特定测试线上了。

膜中的最后一条测试线是控制线。由于参考抗体总是被混合到样本中，因此控制线应该总是能检测到参考抗体与结合化学物质的复合物的存在。如果控制线没有检测到这种复合物，那么这意味着样本没有以正确的方式通过测试条，所以该次测试应该被视为无效。

当样本充满膜后，它会继续流向吸收板，吸收板起到吸液芯的作用。吸收板吸收样本，这种吸力驱使样本通过测试条，直到吸收板内完全充满样本。

模型预览

在本系列的下一篇博文中，我们将展示LFA设备的两种模型。这些模型揭示了一些由从事这些测试设计的科学家通过实验观察到的特征。其中一个特征是：流动如何取决于液体样本孔隙体积的饱和度？敬请关注后续博文！

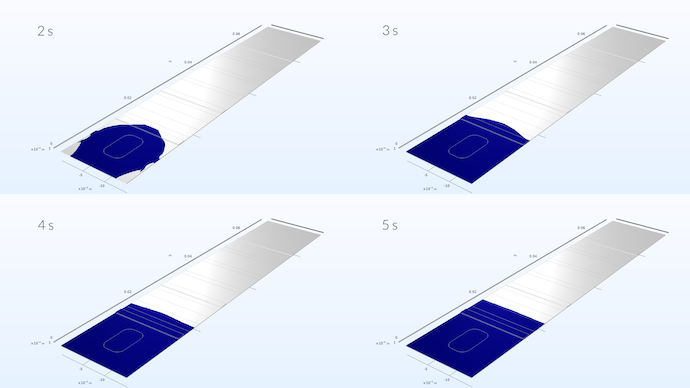
测试条中液体样本的扩散。模拟显示，一旦样本达到连接板的三分之一，样本就会形成均匀的速度分布。

参考文献

1. T. Kilic, R. Weissleder, and H. Lee, “Molecular and Immunological Diagnostic Tests of COVID-19: Current Status and Challenges”, iScience, vol. 23, no. 101406, 2020, (https://www.cell.com/iscience/pdf/S2589-0042(20)30596-4.pdf).
2. B.G. Andryukov, “Six decades of lateral flow immunoassay: from determining metabolic markers to diagnosing COVID-19”, AIMS Microbiology, vol. 6, no. 3, pp. 280–304, 2020, (https://pubmed.ncbi.nlm.nih.gov/33134745/).
3. “Rapid Lateral Flow Test Strips, Considerations for Product Development”, Merck Millipore, 2013 EMD Millipore Corporation, Billerica, MA, USA.

拥有一种先进的多孔介质仿真技术是许多行业的刚性需求。自 COMSOL Multiphysics^® 软件 5.5 版本起推出的附加产品多孔介质流模块可以满足用户的这一需求：定量研究多孔介质中的质量、动量和能量传递，其应用领域包括燃料电池、纸浆和纸张干燥、食品生产和过滤等。

多孔介质流仿真

在诸如化学工程、土木工程和核工程等众多工程领域中，模拟多孔介质中的质量、动量和能量流动十分常见。多孔介质流模块提供了一套全面的物理场接口，旨在帮助工程师和科研人员模拟多孔介质中不同类型的物理过程。

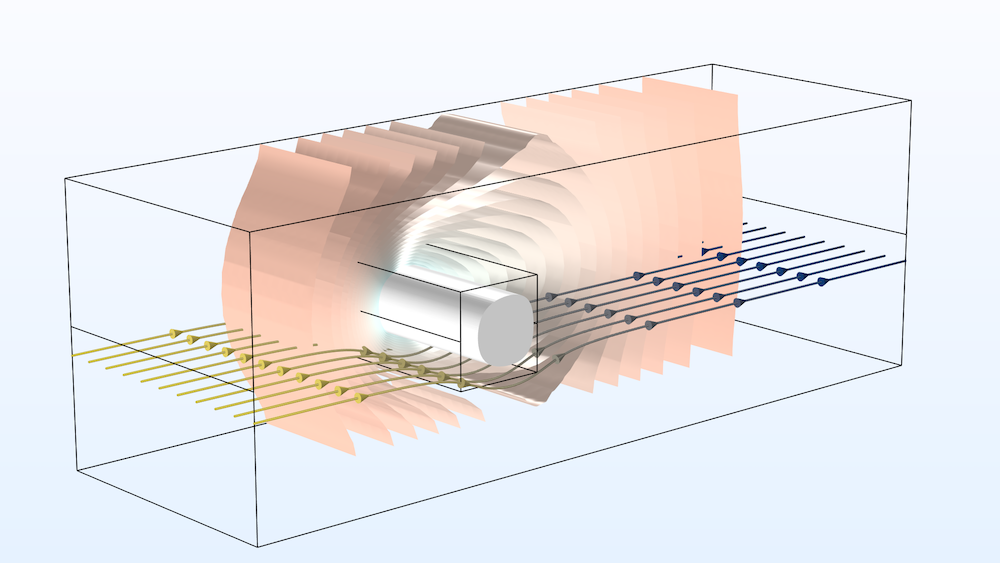
使用多孔介质流模块模拟的冷冻夹杂物。

借助多孔介质流模块，采矿、生物医学和食品工业等许多不同行业的工程师能够在用户友好的建模环境中分析和优化其工作流程。例如，多孔介质中的多相输运等问题可以通过完整的多物理场方法进行求解。

用户使用多孔介质流模块的多物理场功能可以计算：

• 多孔介质中的非等温流动
• 多组分体系的有效传递属性
• 多孔弹性
• 水分和化学物质的运输

接下来，让我们详细了解这些应用领域中的一些问题……

多孔介质中的多相传递

多孔介质流模块包括可以模拟多孔介质中两相或任意多相流动。用户可以指定不同相间的相对渗透率和毛细压强等多孔介质属性，模拟多孔介质中的芯吸、水分输运或其他传递现象。

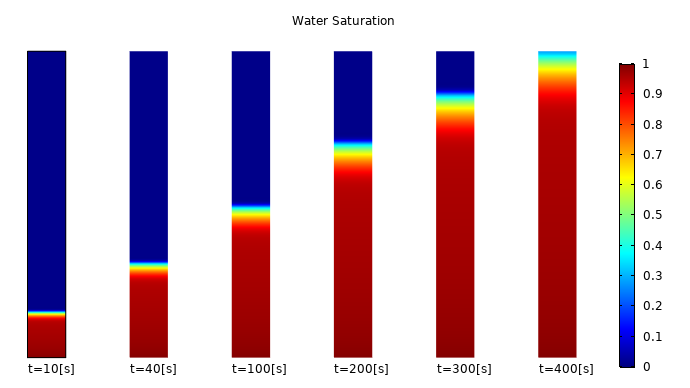
纸条芯吸模型（一种多孔介质）的模拟结果。

当干燥的纸条与液体接触时，由于纸条将在毛细管力的作用下吸收液体，吸收过程将一直持续到重力与毛细压力平衡。在此示例中，水和空气两种相通过 达西定律 和 多孔介质相传递 接口的耦合相互作用。

多孔介质中的非达西流

在之前的博客中，我们讨论了包括达西定律 和 Brinkman 方程 接口在内的，可用于模拟饱和及变饱和多孔介质中的流动的物理场接口。

达西定律适用于模拟孔隙间隙速度较低的场景，即雷诺数低于100。对于较高的速度和雷诺数，可以在动量方程中添加附加的非线性修正。多孔介质流模块可以模拟流体的速度场与压力梯度存在非线性关系的非达西流体。

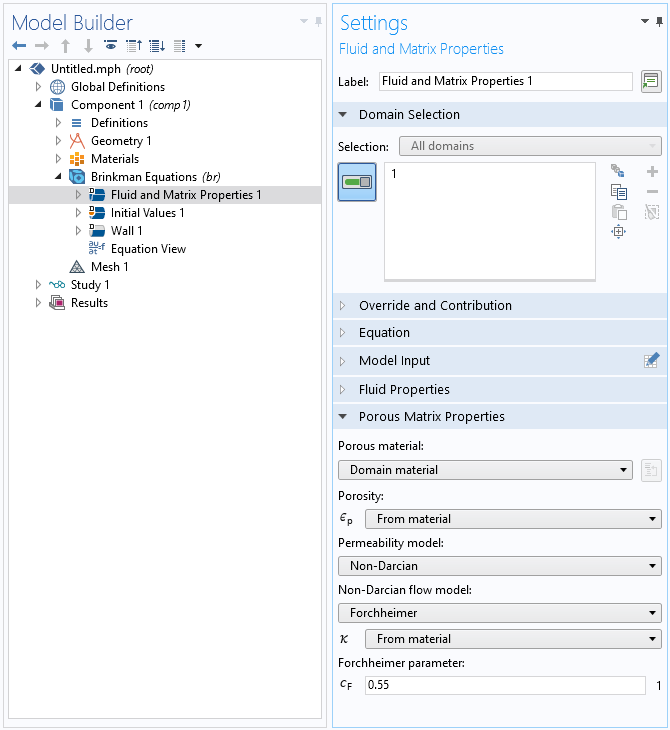
可用于模拟多孔介质中非达西流的选项包括达西定律和多孔介质多相流接口的 Forchheimer，Ergun，Burke-Plummer 和 Klinkenberg 模型，Brinkman 方程的 Forchheimer 和 Ergun 模型。

多孔介质传热的局部热平衡和非平衡

多孔介质中的热量传递可能包含由 传导、对流和弥散等引起，并且必须考虑固相和液相的不同的热属性。使用多孔介质流模块，可以采用两种方法来模拟多孔结构中的热量传递：

1. 局部热平衡（LTE），其中固体基体和液相的温度处于局部平衡状态。
2. 局部热非平衡（LTNE），其中固相和液相定义了不同的能量方程，因此需要考虑流-固界面的温差导致的传热效应。

填充床潜热存储模型包含相变效应和局部热非平衡。

多孔介质中的裂隙流动

对于化学、土木和核工程师而言，模拟裂隙多孔介质中的质量、动量和能量传递现象具有重要意义。多孔介质流模块包括用于模拟多孔介质几何内部边界上压力、温度和化学物质传递的物理场接口。这种近似方法避免了对具有厚度的实际裂隙进行网格划分，以及由此产生的计算资源消耗。

活性炭芯陶瓷滤水器模型的模拟结果。

陶瓷滤水器常用于去除饮用水中的化学物质和颗粒。陶瓷芯中的小孔可以去除大颗粒和细菌，而活性炭可以去除重金属和氯。如果陶瓷芯中存在裂隙，就可能会导致饮用水中残留污染物。

多孔介质的相变

多孔介质流模块还包括一个定制的用于模拟多孔介质中相变的接口。典型的相变现象包括冰融化成水或建筑材料中蒸汽的蒸发和冷凝。

下一步

点击下方按钮，了解模拟多孔介质中的质量、动量和能量传输专用功能的更多信息：

从大型地质区域到纳米级结构，所有长度尺度上都会发生多孔材料中的流动。虽然许多应用都可以用达西定律来模拟，但是在工业应用中，速度场和压力梯度之间的关系不再是线性的，达西定律不能提供准确的结果。在这篇博客中，我们将更深入的研究多孔介质中可能出现的不同流动状态，以及如何描述它们。

在微观尺度上模拟多孔介质中的流动

为了深入理解多孔材料中的流动特征，我们有必要仔细研究它的微观结构。这不仅使我们能更深入的理解多孔材料，也有信心使用宏观方法来模拟多孔材料中的流动。

下面的动画显示了一个尺寸为 2 cm × 2 cm × 6 cm 的复杂多孔结构，以及使用线性纳维-斯托克斯方程计算的流型。

一个小的多孔块中的流型。

这个多孔块中有流速低的区域和流速高的区域，也有根本不发生流动的区域。即使多孔结构是不规则的，但当其被放大多孔，同一样本中的不同区域的流动特性是相同的。这种结构被称为 表征体元（REV）。采用表征体元的平均值可以得到一个宏观方程，详见下一节内容。

为了表征流动并获得有关宏观方程的信息，下面几个数值很重要：

• 孔隙率 ，描述孔隙体积与总体积的比率，可以通过几何结构计算获得
• 沿流动方向（纵向）的压降 ，可以通过计算或预定义获得
• 表观速度 ，或通过结构的体积流率，由 (m³/s)除以总横截面积 (m² )获得。

宏观尺度上的流动

达西定律是描述多孔材料流动的基本方程，它最初只是一个经验定律，后来在理论上由纳维-斯托克斯方程推导出。它描述了速度场 (m/s)与压力梯度 （Pa）之间的线性关系。

(1)

其中，(m²) 是多孔介质的渗透率， (Pa·s) 是流体的动力黏度。

在如填充床或颗粒土等规则结构中，渗透性可以由 Kozeny-Carman 关系推导：

(2)

其中， (m) 表示有效粒径（对于球形颗粒，它等于球体直径）。

线性达西定律适用于低速流动。与自由流动一样，多孔介质中的雷诺数

(3)

也用于表征流动，式中 (m) 是特征长度尺度。

对于 ，线性达西定律是有效的。因此 孔隙尺度流动可以被描述为蠕动流，其中惯性力比黏性力小得多。地下水流和其他低速和（或）高黏度流动的应用就是这种情况。然而，在大多数工业应用中，例如在填充床反应器、过滤器甚至食品工业中，都涉及到更高的流速，包括黏度非常低的气流。在这些应用中，仅使用 方程1 是无法描述的，还必须引入非线性项。这被称为非达西流，表述如下：

很明显，可以看到等式右侧的左边项对应于达西定律。至于非线性项，由 Forchheimer 方程可知，

(4)

其中， 是惯性阻力系数， 是 Forchheimer（无量纲）参数。

对于填充床应用，可以使用 Ergun 方程描述，使用以下关系式：

(5)

在高雷诺数下，黏性效应比惯性效应小，并且 Ergun 方程中的非线性项占主导地位，被称为 Burke-Plummer 方程。

这些方程已经可以很好地描述多孔介质中的非线性流动，但下面的图表会更便于观察。为了更好地观察，我们以平均粒径为 (mm) 的填充床中速度与压降的关系为例来说明。在下图中，Kozeny-Carman 描述了线性极限，Burke-Plummer 描述了二次极限。Ergun 和 Forchheimer 方程都可以描述线性和二次极限，两者之间的区别在于是根据 方程2 还是 方程5 计算渗透率的。

Kozeny-Carman、Forchheimer、Ergun 和 Burke-Plummer 关系的比较。

除上述考虑的情况之外，还有一种用于处理特殊气体流动的完全不同的非达西定律，即气体分子的平均自由程与孔隙尺寸大致相同的情况。在这种情况下，气体分子与孔壁的碰撞比与其他情况下气体分子的碰撞更频繁。这就是所谓的滑移流状态，从纳米材料到气体储藏模拟。其典型应用涉及范围很广。在这种情况下，渗透率方程为

(6)

其中， 是绝对压力 (Pa) ， 是高压下的渗透率 (m²)，相较于分子之间的碰撞，分子与壁的碰撞与可以忽略不计。

Klinkenberg 参数 (Pa) 取决于多孔介质的渗透率，可以在文献中查到 （参考文献 1）。

COMSOL 中的多孔介质流模块包含了上述所有渗透率模型。Forchheimer 和 Kozeny-Carman 方程在多孔介质流动的其他模块中也可以使用。

COMSOL 软件中渗透率关系的所在位置。

非达西流，从微观到宏观尺度

那么，如何将这两种方法联系起来呢？第一个模型，即表征体元，给出了速度与压力梯度的关系，也可以确定孔隙率和渗透率。同样，还可以观察不同数量级的压降流动行为。由于结构复杂，多孔结构模拟的计算成本相对较高，因此必须合理地求解。此外，与平均方程（方程2–方程 6）相比，纳维-斯托克斯方程本身就更为复杂。

使用宏观方法可以得到非常好的近似值。达西定律适用于小压降和低速流动，而 Burke–Plummer 方程适用于大压降和高速流动。

Forchheimer 方程可以很好地计算过渡区域。在本文的示例中，将 Forchheimer 方程与来自微观模型的数据相拟合，获得了 Forchheimer 参数 ，该数据通常是通过实验确定的。

结束语

在这篇博客中，我们从微观和宏观层面研究了多孔介质中的流动，并演示了宏观方法可以得到非常好的近似值，并且有各自的适用领域。

多孔微通道散热器的优化案例模型就是使用 Forchheimer 方程模拟的一个工业应用示例。

在讨论了多孔介质中的流动之后，接下来我们将讨论多孔介质中的传热，敬请期待！

动手尝试

单击下面的按钮，进入 COMSOL 案例库，您可以下载 MPH 文件，尝试自己动手模拟文中介绍的案例模型。

参考文献

1. Y. Wu, K. Pruess, and P. Persoff, “Gas Flow in Porous Media With Klinkenberg Effects“, Transport in Porous Media, vol. 32, pp. 117–137, 1998.
2. J. Bear, Dynamics of Fluids in Porous Media, Courier Corporation, 1988.

通过模拟气候变化的影响，科学家可以设计解决方案以减轻其潜在影响。气候学家希望可以解决北方寒带地区多年冻土的融化问题，并且能对这些地区产生影响和很好的正反馈。InterFrost 项目设计，以测试，评估。此处的示例通过使用热-水力方法对高于零度以上的土壤中融化的冷冻夹杂物进行建模，并与 InterFrost 标准案例进行比较。

什么是冷冻夹杂物？

冷冻夹杂物是指固体物质内部的一些冷冻物体，就像披萨（内部）需要微波加热后才能食用。不连续或零星的永久冻土是另一个例子：在多孔（但仍然是固体）土壤内部中冻结的冰块。水中的冰块属于另一类是冷冻夹杂物（冰块没有被固定）。

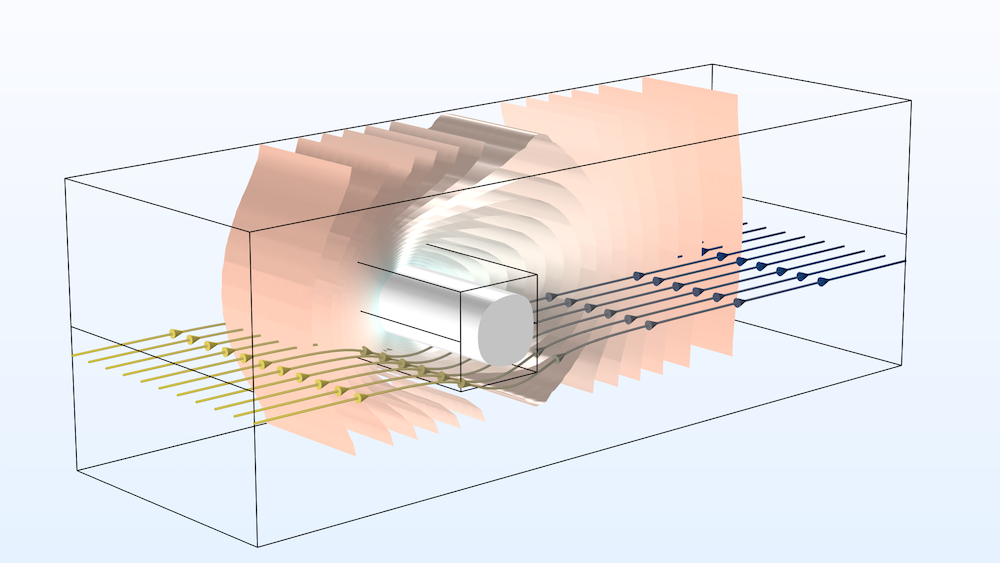
冷冻夹杂物的 3D 图：结果显示 9 小时后（白色表面）包裹体内的冰块、速度流线（颜色表示水头）和周围温度（等值面）。

对 COMSOL Multiphysics® 中的冻结夹杂物建模

在此示例中，您可以模拟冷冻夹杂物从冰到水这一相变过程。它是如何融化的？融化需要多长时间？还需要多长时间才能将所有冷水从冰冻的土壤中排出？

这种特定的模拟不仅对于气候学家和地球科学家特别有用，而且对于任何分析多孔介质中的相变感兴趣的人也很有用。在本教程中，我们考虑永久冻土。

给定的几何图形如下所示。这条通道长3米，宽1米。冷冻物长 33.3 厘米，位于（x，y）=（1，0.5）处，温度为 -5°C 。由于对称性，我们只模拟了通道的下半部分。

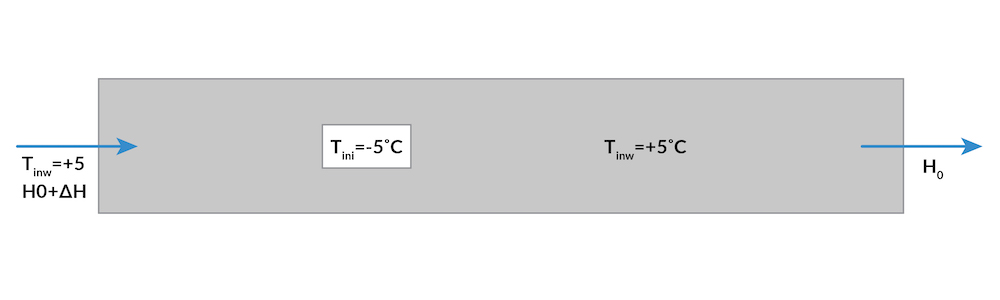
模型的几何形状，显示了初始温度分布和边界条件（零传导通量，零通量）。

有一些给定的数字，包括冷冻夹杂物的温度、水的温度、几何尺寸和水头的梯度。

此示例中有几个方程，最著名的是达西定律。您还可以假设以下内容：

• 传热方程不考虑热弥散
• 水的密度恒定不变
• 水动力粘度恒定不变

分析仿真结果

冷冻夹杂物仅在大约20个小时后（模拟时间）融化了。但是，需要整整 56 个小时的模拟时间才能将较低的温度从通道中全部对流出去（这是因为多孔介质比自由介质更能保持温度）。让我们来看一下模拟结果…

9小时后，土壤中仍可见明显的冷冻夹杂物。

面图显示了 9 小时后的温度分布。

56 个小时后，冰完全融化，较低的温度几乎脱离了通道。

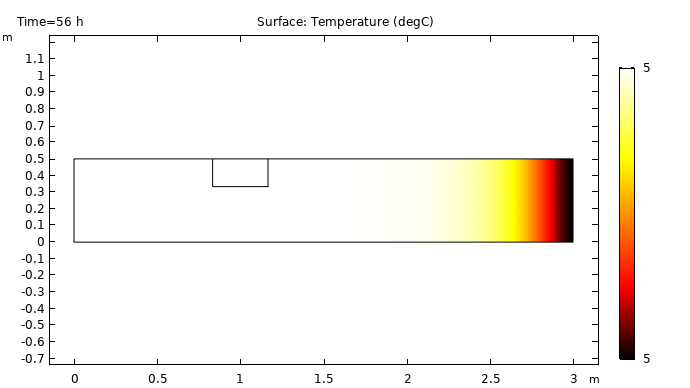
面图显示了 56 个小时后的温度分布。

尽管此标准模型只是一个简单的示例，但它表明研究人员可以通过仿真来分析相似或更复杂的问题。例如，如果冷冻夹杂物不是矩形而是正弦形状变化的，该怎么办？此外，模拟这样的问题可以帮助气候学家确定冰何时融化并导致水饱和，这将会引发许多地质问题。

第二种情况

为了使事情变得更有趣，让我们看看如果土壤中有两个冰块会发生什么。在实际情况下，多年冻土中会有许多冷冻夹杂物。首先，在几何图形中添加另一个冰块。

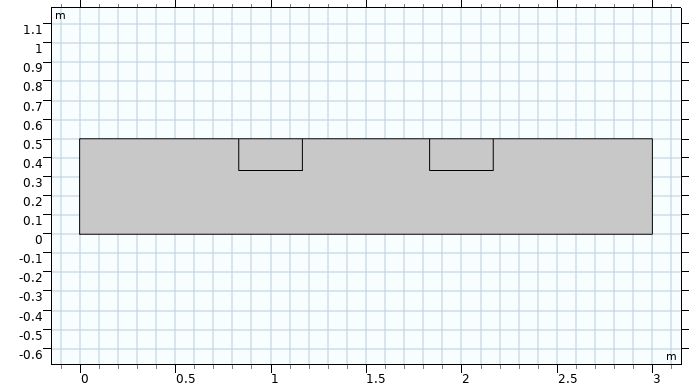
现在，让我们再次运行仿真程序。您认为会发生什么？

从上面的动画中我们可以看到，冰块最初以相同的速度融化，但是第二个冰块的融化速度在大约 9 小时后变慢了。您可以观察温度梯度的变化以了解原因。

起初，这些冰块彼此独立，各自融化。

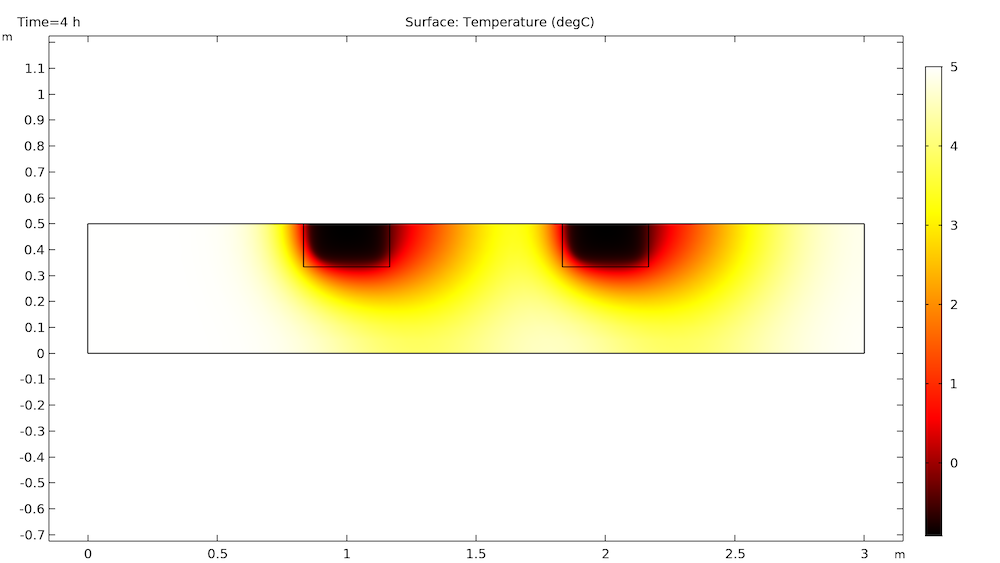
一段时间后，第一个冰块的低温会向下移动到第二个冰块处。这降低了第二个冰块周围的温差，进而降低了其融化的速率。如下图所示，这在 18 小时非常清楚。

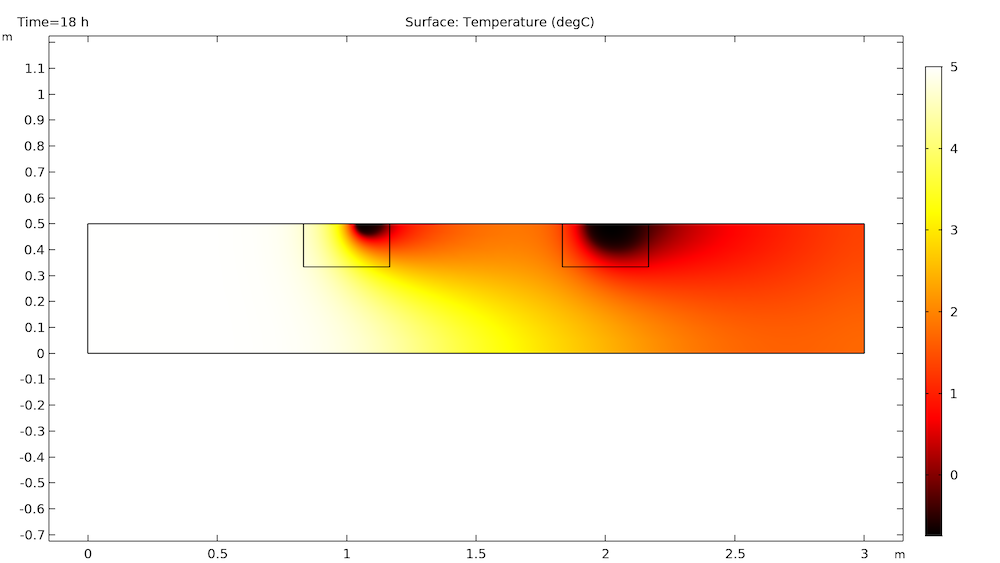
第一个冰块在 21 个小时后融化，但是第二个冰块还有一段路要走，并且它仍会受到第一个冰块对其造成的温度梯度的影响。

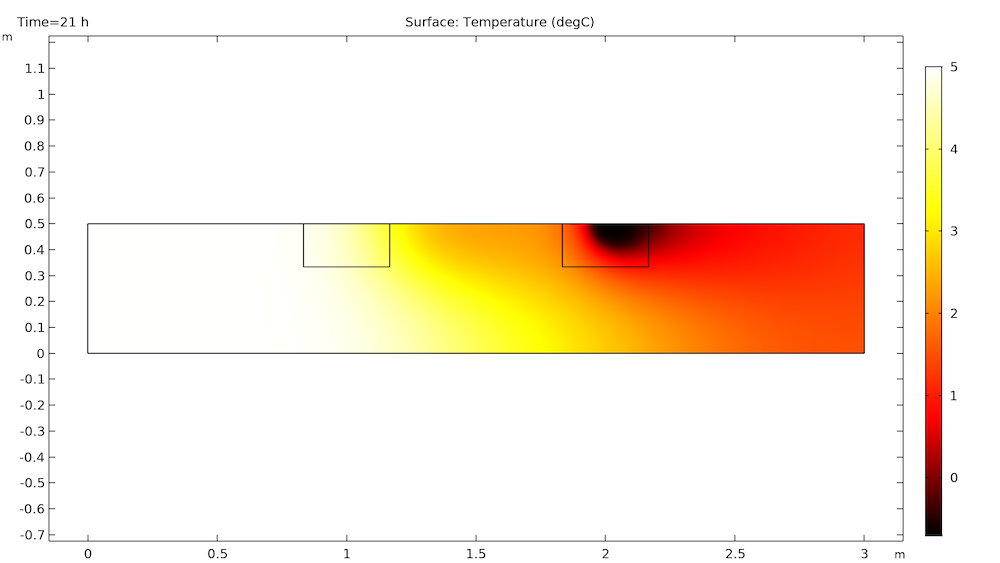
第二个冰块融化需要 29 个小时（第一个冰块融化后的第 9 个小时），低温从通道中对流出需要 56 个小时。

结论

冷冻夹杂物的融化可能很难通过解析的方法来解决，但是可以使用热-水力方法来模拟简单或复杂的问题。如该标准模型，后续示例和 InterFrost 项目所示，仿真是一种强大的工具，可用于对永久冻土融化进行建模并预测北方地区气候变化的影响。

下面是如何使用 COMSOL Multiphysics 来创建有关环境问题的模型和示例：

• 模拟人工地面冻结方法
• 预测堤防结构的变形

通过单击下面的按钮，尝试使用 “冷冻物” 教程模型自己对冷冻夹杂物的融化进行建模。这样做将带您到案例库中，在那里您可以下载其他 PDF 文档和 MPH 文件（带有 COMSOL Access 帐户和有效的软件许可证）。

复杂地质结构的三维知识以及将其整合到水文地质模型中，是研究不同尺度水力动力学过程的先决条件。这篇博文介绍了将这类结构从三维地质软件整合到 COMSOL Multiphysics^® 软件中的地下水流数值模型的过程中所面临的不同挑战。

使用 COMSOL Multiphysics^® 模拟地下水

市场上有大量模拟地下水的专用软件包，其中有很多采用结构化网格，并要求从整个地质模型的 z 方向上固定层数构建地质。但是，在千米尺度的复杂地质结构中，断层带可能会以任意角度出现。尽管 COMSOL^® 软件尚未广泛应用于地下水模拟问题，但它允许导入更复杂的几何、使用非结构化网格以及将断层带视为水力裂缝，因此可以在地下水模拟中使用。

地质三维模拟越来越多地被用来更好地理解空间结构关系。图1显示了瑞士汝拉山脉区域尺度（约 4km x 4km）的地质模型。该项目的主要研究目的是（拟建）隧道对该地区频繁出现的含硬石膏层位对地下水循环的影响，以及在硬石膏转换成石膏的过程中可能出现的膨胀问题。

图1 放大 4km x 4km 后的复杂地质三维模型（在 GOCAD^® 软件中模拟）。将此模型导入 COMSOL Multiphysics 后，将得到 37 个域和 386 个面。

将地质结构导入 COMSOL^®

将在 GOCAD^® 地质建模软件中准备的区域尺度的结构地质三维模型作为 COMSOL^® 地下水模型的起点，然后将不同的地质表面转移到 COMSOL Multiphysics 中。刚开始，我们尝试基于 DXF 或 STL 文件在两个软件之间进行几何传输，结果导致后续处理步骤非常复杂。因此，我们采用了一种特定的策略来导入复杂的地质模型：

1. 首先，从 GOCAD^® 将不同的地质表面导出为 xyz ASCII 文件，然后使用插值函数将其导入 COMSOL Multiphysics^®。我们必须找到一个合适的分辨率，因为太少的点会导致信息丢失，而太多的点会导致文件过大。
2. 然后，在几何特征的参数化面中使用插值函数。仅通过这两个步骤就可以导入简单的几何，但是对于更复杂的几何，则需要第三步。
3. 插值函数总是定义在一个矩形的基础上，但实际上并非所有层边界或断层都是这样。因此，必须使用布尔操作修剪相交曲面。由于插值和布尔操作可能会更改原始几何图形，因此我们总是在视觉上将经过处理的面与 GOCAD^® 中的原始几何图形进行比较。此外，我们系统地分析了点与面之间的距离并调整了设置，直到达到足够的精度（米量级）为止。

分辨率

图2 从插值点文件创建的参数化面。

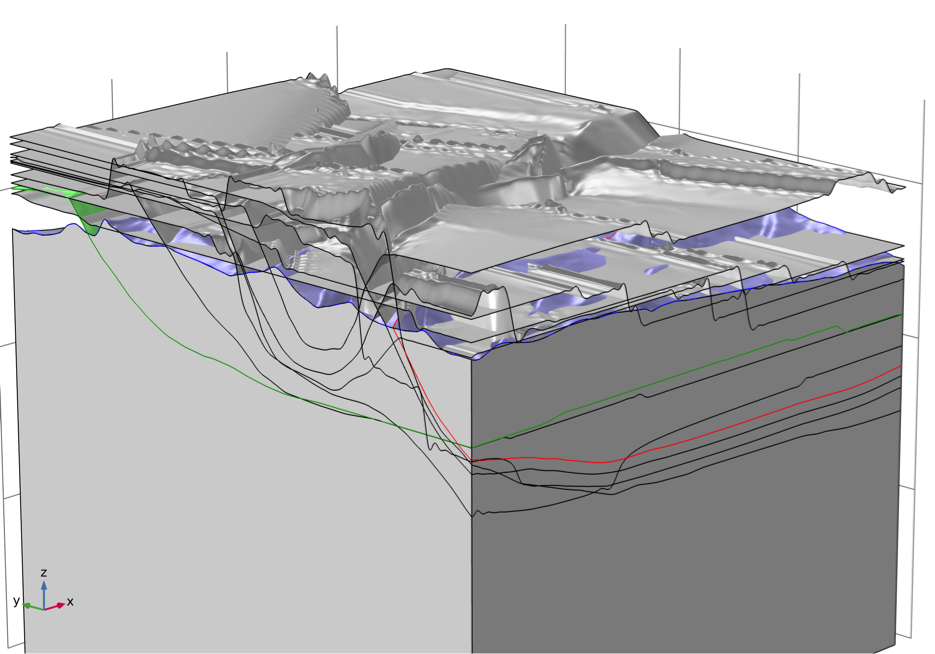
图3 必须逐步切割重新创建的面。左：添加边界框。右：红色面已经与地形相交（蓝色）。绿色面仍必须被地形和红色面修剪。

创建模型几何形状后，将由三个隧道管以及连接轴和通风井组成的隧道系统整合到COMSOL模型中。在图4中，隧道和局部模型的周长（用于研究特定隧道截面）用蓝色突出显示。

图4 具有集成隧道和局部模型周长（以蓝色突出显示）的模型几何结果（可以沿着地形脊切割模型，以更好地定义边界条件）。

设置数值模型

受重力驱动的地下水循环由大尺度区域中的弱透水层和含水层几何序列控制。水力势能的大尺度分布直接取决于地形。图5示出了如何将各个地层信息组合成水力相似的单元。
 

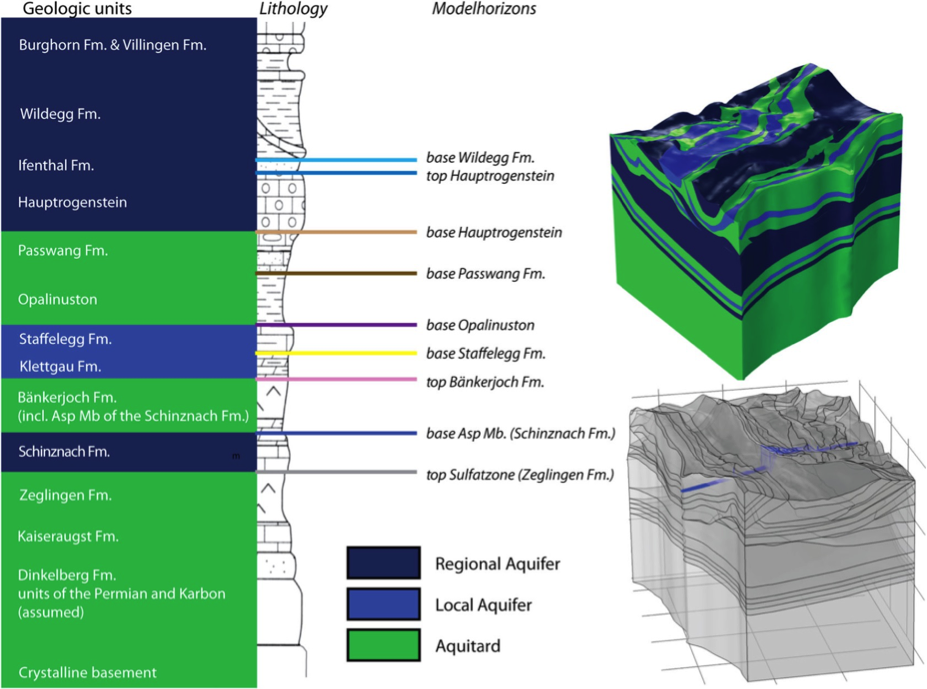
图5 将地质信息整合到水力单元中（点击此处，参考地质术语）。右下：隧道衬砌和位于区域尺度模型中的局部尺度模型（蓝色）。

仿真结果

由流动方向箭头的变化，我们可以直观地看出含水层、弱透水层和隧道几何形状的影响（图6）。通过将地质单元划分为区域和局部含水层以及含水层来简化地质模型，同时需要关注不同岩性单元的主要水力。但是，我们仍然可以从区域模型中获得有价值的基本信息，将来可以在监测数据的修正数据的基础上对这些信息进行调整。将复杂的地质信息整合到数值地下水流模型中，使我们能够在隧道局部尺度以三维视图的形式计算地下水循环。利用当地正在进行的水文地质模型计算，可以比较不同的隧道设计（例如排水系统），这有助于在不同的项目阶段为利益相关者做出决策。
 

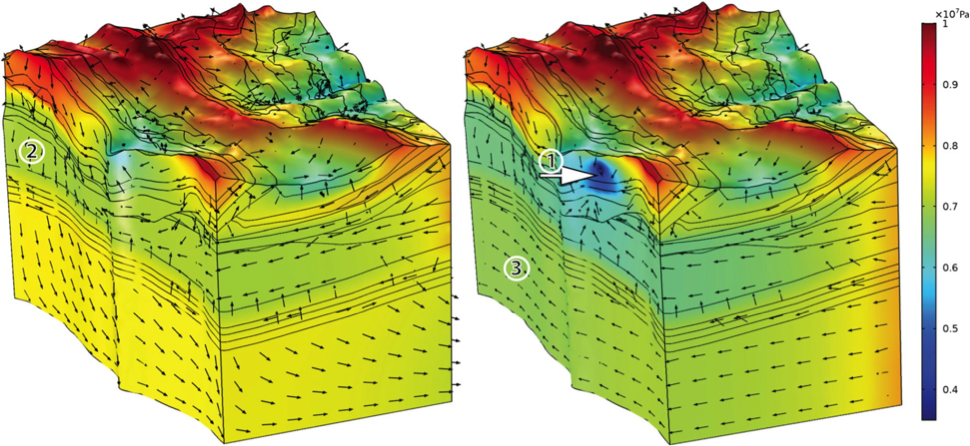
图6 区域尺度地下水模拟结果。颜色显示了以帕斯卡为单位的水力压力分布。箭头表示流动方向。左图显示了没有隧道的模型，右图显示的是大气压力下有隧道的模型。（1）隧道内大气边界条件引起的压力降低；地下水流向改变并指向隧道。（2）而且，较远的区域（在区域含水层中）会产生很大的压力损失。（3）在较深的区域，由于该区域为弱透水层，压力条件甚至地下水的流动方向也会发生变化；但是，流速（图中未示出）极低。
 

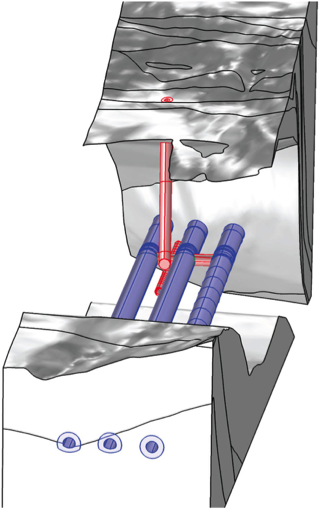
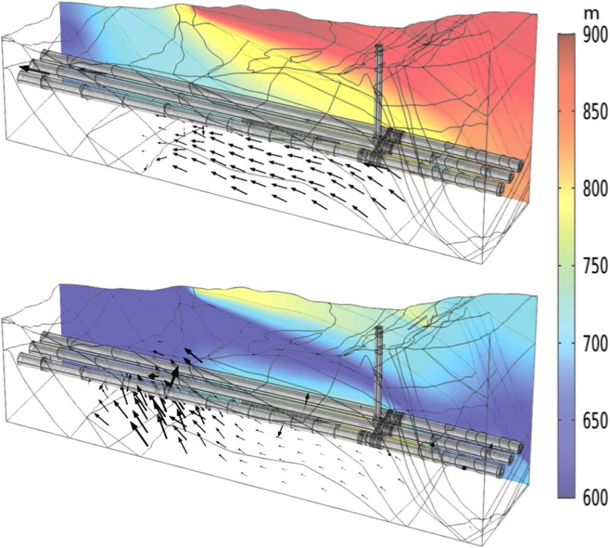
图7 左图：隧道周围开挖扰动区域的详细局部模型（蓝色表示隧道管，红色表示通风井和连接管）。右图：给定情境下局部模型的结果。颜色表示压力水头的分布，箭头表示主要的地下水流（达西速度以对数刻度表示）。

参考文献

1. S. Scheidler, B. Anders, C. Regli, S. Bolay, P. Huggenberger, “Geothermal use of an Alpine aquifer – Davos pilot study,” Grundwasser (2019) DOI: 10.1007/s00767-019-00433-y.
2. S. Scheidler, P. Huggenberger, C. Butscher, H. Dresmann, “Tools to simulate changes in hydraulic flow systems in complex geological settings affected by tunnel excavation,” B Eng Geol Environ 78, 969–980 (2019).
3. C. Butscher, S. Scheidler, H. Farhadian, H. Dresmann, P. Huggenberger, “Swelling potential of clay-sulfate rocks in tunneling in complex geological settings and impact of hydraulic measures assessed by 3D groundwater modeling,” Eng Geol 221, 143–153 (2017).

关于作者

Dipl. Hyd. Stefan Scheidler，在德国布雷斯高的弗赖堡大学研究水文学，自2006年以来，他一直是巴塞尔大学应用与环境地质学（Applied and Environmental Geology ，AUG）研究组的科学家。他的工作重点之一是地下系统的三维地质和水文地质建模。AUG 开发的工具是讨论可持续地下规划（包括地下水资源管理）的重要基础。
 

 
更多详细内容，请参见 Dipl. Hyd. Scheidler 在 2018 年洛桑 COMSOL 用户年会上的相关研究：“区域地下水建模- 将地质结构整合到数值模型中”。

GOCAD 是 Paradigm 的注册商标。Autodesk，Autodesk 徽标和 DXF 是 Autodesk ， Inc. 和/或其在美国和/或其他国家/地区的子公司和/或分支机构的注册商标或商标。

地下水是灌溉水和饮用水的重要来源，因此保持其纯净性至关重要。然而，一旦进入污染物，将它们排出就不是那么容易了。建立从地下水中去除污染物的系统，需要了解非混相流体在土壤中迁移的复杂行为。工程师可以使用 COMSOL^® 软件中的相传递功能来模拟这种行为。

预测地下流体的迁移

流体，特别是非混相流体在地下的迁移行为对许多行业都很重要。研究人员曾经对这种传递方式进行过研究，用于改进石油的开采和回收方法。如今，他们更关注非混相流体对环境产生的负面影响。例如，废弃物管理和环境保护等行业的工程师正在设计能够更好地预防、检测和清理土壤中污染物的系统。如果不加以控制，污染物就会进入地下水，并影响农作物的质量。

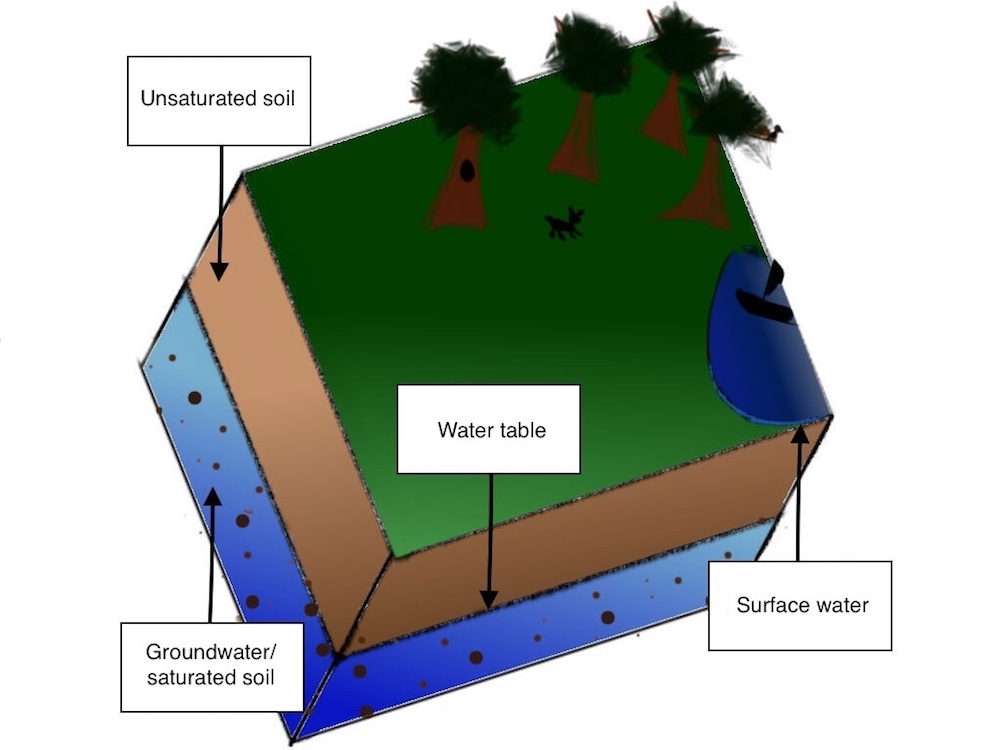
地下水插图。

然而，由于涉及过程的复杂性和非水相液体的性质，理解流体流动是一件困难的事情。油和其他非水相液体污染物的密度通常与水不同，即使它们混合在一起，也会分开流动（多相流）。非水相液体还可能会被困在淤泥和黏土等渗透性低的土壤区域，从而更难被检测和清除。此外，非混相流体如何流过土壤（以及任何低渗透区）取决于土壤的饱和度。

为了深入理解流体在土壤中的流动，工程师可以借助数值仿真技术进行模拟与分析。本文，我们来看一个这方面的示例模型：含有低渗透性晶体的多孔介质中的多相流模拟。

模拟多孔介质中的多相流

该示例模型由一个圆形域组成，用于表征中间有一个低渗透性晶体的多孔介质。由于轴对称性，我们只需要建立一个二维横截面模型，这可以帮助降低仿真的计算成本。首先，让比非水相液体轻的流体（比方说水）充满整个域。模拟开始后，较重的非水相液体通过顶部的小孔以恒定且均匀的质量通量进入该域，持续 100 分钟。

在这里，我们不会详细介绍所有的模拟细节，您可以在 COMSOL 案例库中的低渗透性晶体上方的两相流教程模型，下载相关的 MPH 文件，查看流体和土壤的属性。

我们可以使用 COMSOL Multiphysics^® 软件中的 CFD 模块和地下水流模块中的相传递功能，轻松模拟两相流。使用 多孔介质相传递 接口，可以分析非混相的流体如何在土壤中流动，从而确定饱和度，并考虑相界面发生的微观现象以及重力的影响。还可以通过 多孔介质多相流 多物理场耦合节点将这个接口的功能与 达西定律 接口耦合，更加方便地模拟多孔介质中多相流体的流动和传递。

虽然本文示例中没有使用，但我们也可以使用 相传递 接口，而无需追踪它们之间的界面，来模拟自由流动的多相流动，从而使计算要求低于其他方法。

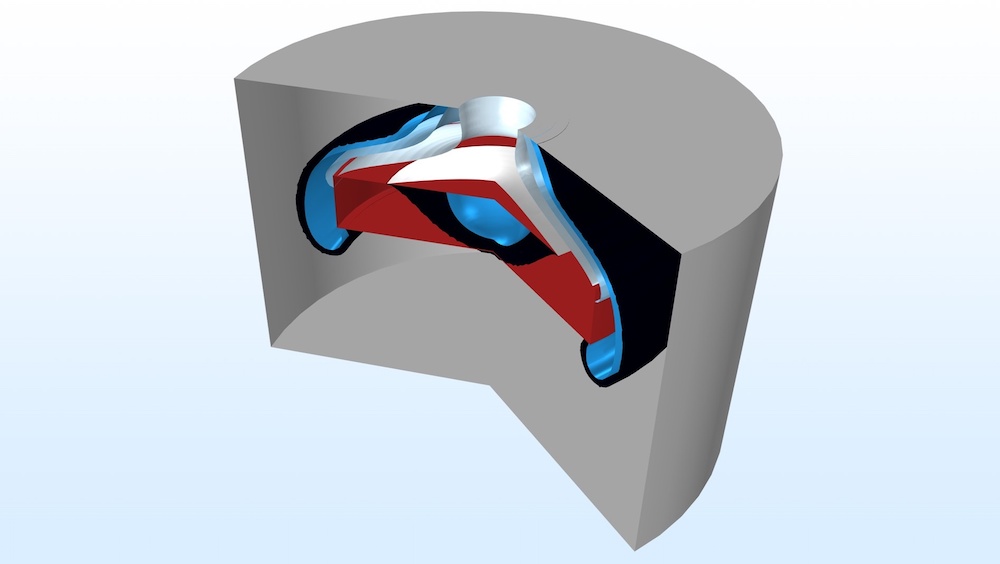
仿真结果显示了低渗透性晶体周围的两相流。

预期开始时重相在会在低渗透性区域周围流动，但不会渗透进去，因为晶体的入口毛细管压力高于周围土壤的压力，这意味着只有当其饱和度达到临界值时，密度更大的非润湿流体才能进入晶体。我们可以使用 多孔介质不连续性 边界条件来模拟此过程，该功能允许土壤-晶体界面不连续，有助于确定临界饱和度。

可视化结果

运行模拟后，我们可以看到重相的流动与预期的结果一致。流体不会立即渗入晶体，而是仅在其周围的土壤达到临界饱和度时才进入，这发生在大约第 12 分钟。约一个小时后，重相到达晶体的底部。

正如文中的示例所示，工程师可以使用 COMSOL Multiphysics 中的相传递功能分析单相和多相流体在多孔介质中的传输。通过更透彻地理解其中所涉及的物理过程，他们可以设计出更高效地去除地下水污染、石油开采等系统。

下一步

想尝试自己动手模拟低渗透性晶体上方的两相流教程模型吗？请单击下方按钮进入 COMSOL 案例库，查看文中示例的文档并下载 MPH 文件。

更多资源

• 在 COMSOL 博客上了解有关模拟地下流动的更多信息：
  • 使用仿真 App 提高穿孔井的生产效率和安全性
  • 使用子模型计算多孔介质中的孔隙率和渗透率
  • 借助数值仿真分析多孔结构
• 观看关于模拟采油方法的主题演讲视频

虽然我们的日常生活明显受到水循环中“明亮的”(雨、雪等)部分的影响，但其他循环，比如我们脚下流动的地下水，也同样重要。地下水常用于灌溉和饮用，并影响着自然过程和栖息地。在研究地下水时，了解各种溶质在水中的迁移通常很重要。要预测溶质的迁移，科研人员可以使用多物理场仿真。

通过追踪溶质监测地下水质量

如果能看到地球表面以下，你会看到什么？你将发现大量的淡水，因为地球上大约 30% 的淡水位于地表以下。地下水不像地下河水那样流动，而是像海绵中的水一样充满土壤和岩石颗粒之间的空隙。

地下水示意图。

确保地下水不受污染至关重要。这些水不仅可用于饮用和灌溉，而且还影响着不同栖息地的健康，对河流和溪流的流动也有帮助。工程师们致力于预防地下水遭受污染(可能会伤害人类和野生动物)，并定期监测地下水的流动和健康状态。他们的工作包括检测地下水中的污染物，使用人工示踪物等设备研究地下水的流动和迁移。

为了准确预测污染物和示踪剂等溶质在地下流体中的迁移，环境和地球科学工程师可以使用 COMSOL Multiphysics^® 软件及其附加的地下水流模块进行建模和仿真。借助仿真技术，工程师可以防止地下水被污染以及优化地下水示踪物的设计。

模拟已知地下水流中的溶质迁移

在下面的示例中，我们追踪了一个已知地下水流中的溶质，并考虑了纵向和横向分散性。这些溶质在 1000 天内通过了 16 平方公里的区域。这种特定设置通常用作基准来验证模拟物质迁移的不同方法。在这里，我们使用 Zimmermann 等人在 2001 年发表的一个基准设置。

使用 COMSOL 中的 稀物质传递 接口，求解模型的初始浓度，该浓度遵循高斯分布。

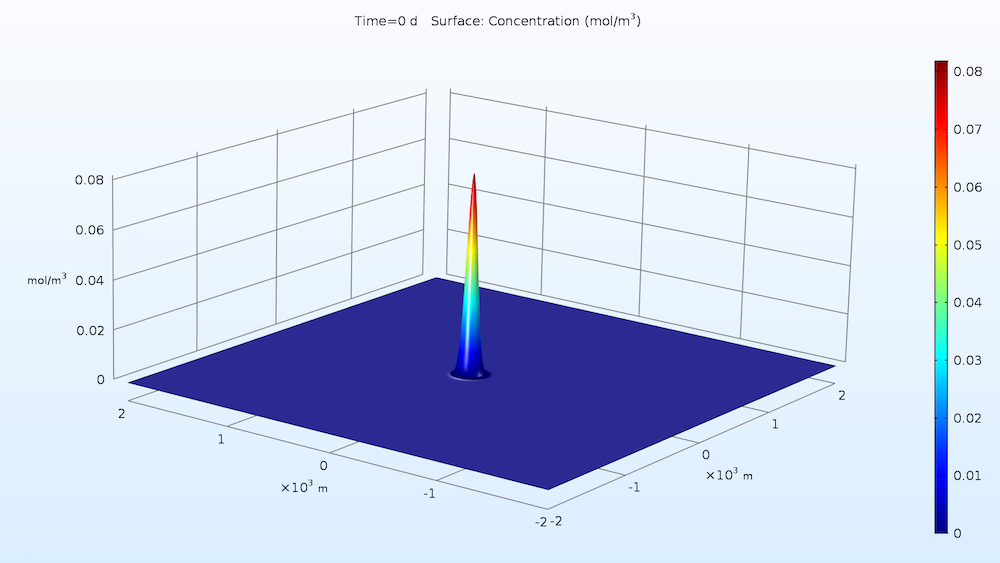
模型几何结构由一个边长为 4 公里的正方形组成。如图所示，初始浓度遵循高斯分布。

为了确认该模型的准确性，我们将其与 Wilson 和 Miller 的解析解（教程文档中的参考文献 1）进行了比较。为此，将他们的解析解在 COMSOL Multiphysics 中定义为一个函数。由于生成的表达式很长并且仅用于比较，我们只需加载一个已经包含解析解的预设文件就可以了。

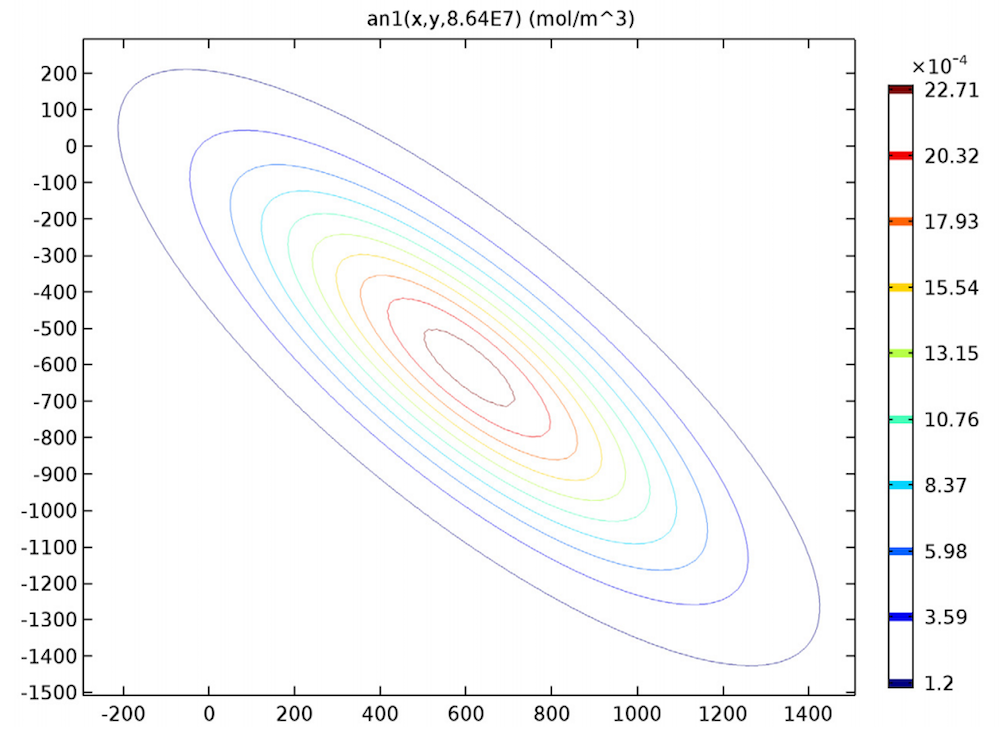
解析解，显示 1000 天后的浓度分布。

仿真结果与解析解的比较

为了将仿真结果与解析结果进行比较，我们生成了一个描绘 1000 天后浓度分布的图。如下图所示，仿真结果（黑色等高线）与解析解(黑色等高线内的白色等高线)一致。

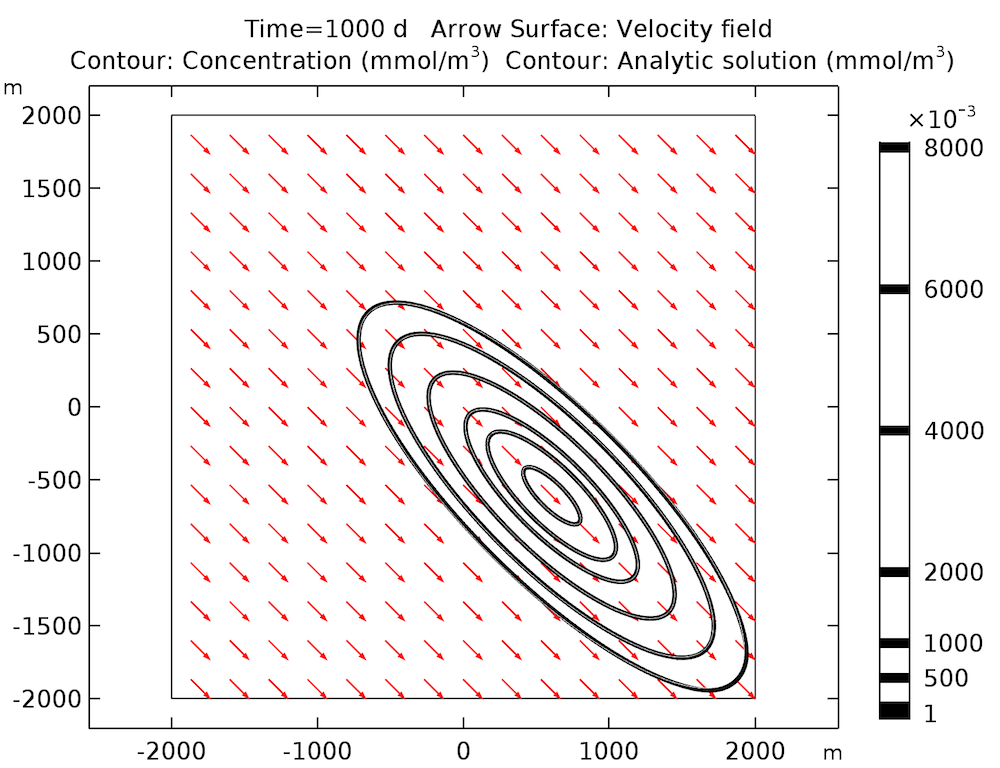
1000 天后的浓度分布。指定的流动方向由红色箭头表示。

溶质迁移穿透模拟和分析结果的表明，二者的结果也一致。这种一致性进一步验证了地下迁移仿真的准确性。

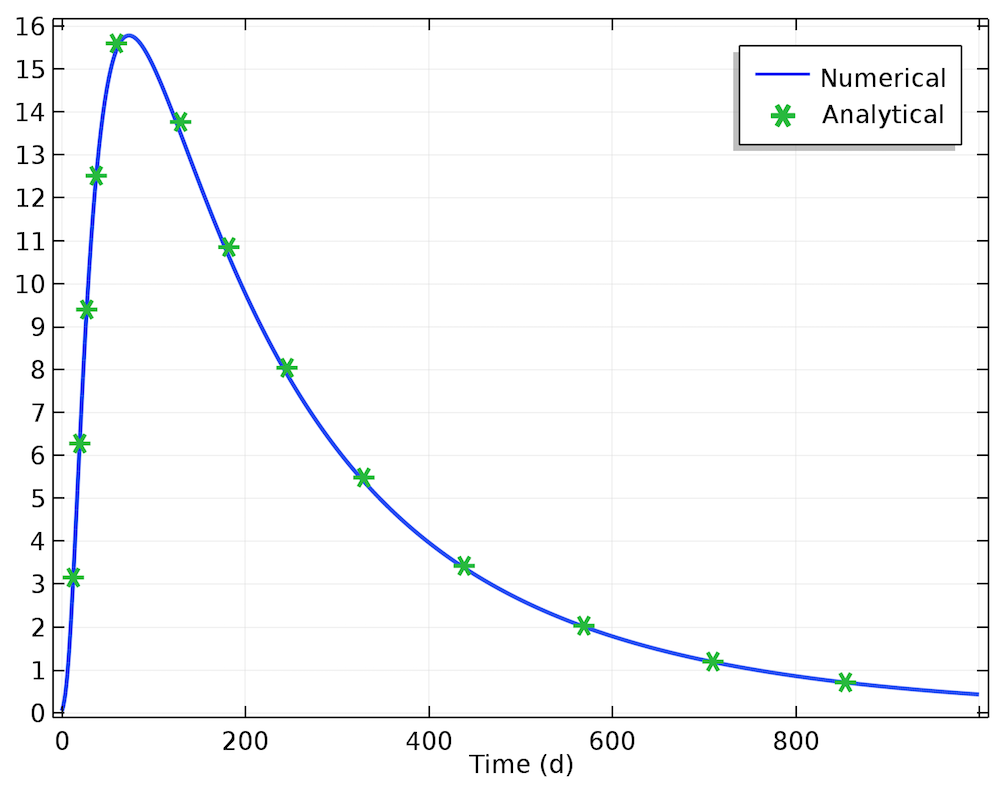
比较了数值解和解析结果的溶质迁移穿透图。

下一步

单击下面的按钮，尝试自己动手模拟文中讨论的溶质迁移模型：

阅读以下博客，了解在 COMSOL Multiphysics® 中模拟地下流动的更多信息

• 我应该使用哪种多孔介质和地下水流接口？
• 使用子模型计算多孔介质中的孔隙率和渗透率
• 通过仿真预测护岸保护结构的变形