声学模块 – COMSOL 博客

利用地震面波寻找埋藏物

Masoud Zarepoor — Wed, 28 May 2025 05:24:40 +0000

特邀博主 Masoud Zarepoor来自苏必利尔湖州立大学（LSSU），他介绍了一种利用弹性面波定位埋藏物的新方法。Zarepoor与他的同事、机械工程教授 Robert Hildebrand，以及一群本科生在振动与声学实验室 (VAL) 研究了这种方法。

地下目标探测器（如金属探测器）的应用前景非常广阔。然而，对于非金属物体，如考古挖掘现场的陶器碎片或塑料包裹的地雷，金属探测器就显得力不从心了。如果我们能从埋藏物的反射波谱中提取出丰富的信息，那么地震面波（也许是勘探现场投掷重物产生的）可能适用于这种情况。

地震面波简介

地震面波（也称“瑞利波”）可能是人们最熟悉的地震波。当然，在地震中，地震面波发生的规模要比这里讨论的应用大得多，但了解这些波的特性仍然很重要。

地震中会有几种不同的波传播，比如压力波或纵波、剪切波和面波。地震面波是地震中最后到达但能量最强的地震波，造成的破坏最大。面波在地震中到达较晚，因为它们沿着地表传播（而不是直接穿过地球），速度明显低于直接穿过地球内部的较弱但传播较快的波。

要充分认识面波在地下目标探测中的潜在应用，我们必须关注面波行为的另外两个基本特征：

在例如地球土壤层和岩石层等分层介质中，这类波的传播速度取决于波长。回到地震的例子，初始地震扰动中混合了许多不同的波长，因此面波不会一次性传播，而是随着时间的推移逐渐扩散，不同波长的波在不同的时刻以不同的速度到达。
虽然被称为“表面”波，但这些波确实会在表面以下引起一些运动。不过，这些运动会随着深度的增加而减弱，因此使用“表面”这个限定词仍然是有道理的。

尤其值得注意的是，波长越长（沿地表测量），运动随深度衰减的速度越慢。

地震现象的规模可能达到数十公里或数百公里。对于较小的规模，例如以米或数十米为尺度的建筑工地评估，其目标可能是确定地基地层和基岩深度，那么速度随波长的变化（上述第 1 点）就具有重要意义。对于波行为的研究催生了一些勘测方法，即通过考虑最能解释观测到的速度变化的模式来推测地表下未见地层的模式。这种形成性技术被称为“面波频谱分析法”（SASW）。

物体定位研究

受 SASW 用作地层学识别技术的启发，研究团队提出对测量到的面波频谱进行同样的分析，只不过现在是在近地表尺度（可能是几十厘米到一米）上对埋藏物体的反射进行分析，这将有助于确定埋藏物体的位置（参考文献 1）。图 1对这一概念进行了展示。

图 1. 基于面波的近地表埋藏物探测系统的概念示意图。

特别的，研究团队假设频谱中与物体深度有关的某些波长可能比其他波长更强（图 2）。比物体深度短得多的波长在物体深度处只会引起轻微的运动（参考上文第 2 点），因此几乎不会产生反射。那些比物体深度长很多的波长也可能反射很弱，原因很简单，与波的尺度相比，物体的特征太微不足道了。至于中等波长，即当波到达足以“看到”物体的深度，但又不会比物体深度长得多的波长，可能会在反射频谱中出现一个峰值。如果假设正确的话，这个峰值的波长（或频率）可以作为物体深度的指数。

图 2.深度推理方法示意图（摘自参考文献 1）。

我们比较熟悉的定位方法，如利用回波返回时间来确定距离（例如使用声纳），以及将面波发射到首选方向以给出方位角，可以补充上述深度推理，并在柱坐标系中获得物体的位置。这些方法仍未经过测试，但对于完善定位方法来说是可行的建议。然而，深度确定是所设想方法中最不传统和最不确定的部分，值得特别关注：作为测试此方法可行性的第一步，研究团队选择使用 COMSOL Multiphysics^® 软件进行模拟。

COMSOL 深度推理研究

我们创建了一个上表面自由、下边界和侧边界无反射的均质介质，作为均匀土壤近表面区域的粗略表示。图 3 显示了在 COMSOL Multiphysics^® 软件中所创建的均质二维介质，并使用三角形单元划分网格。在这个二维模型中，在接近地表的地方，大约位于从左到右的四分之三处有一个空隙。将此空隙作为埋藏物，埋藏物的反射用于测试深度推理方法。在最左侧接近上表面处，一个点力以载波频率循环数次以产生面波，这些波的振幅被调制成脉冲包络的形式。脉冲足够短，以使其在任何从空隙返回的反射到达之前就已完成，因此可以将反射与传出的波清晰地分开（见图 4）。

图 3. COMSOL^® 中的网格，表征了一个包含空隙（右侧，近表面）和激励源（左侧，近表面）的地表土壤区域（摘自参考文献 1）。

图 4 是使用 COMSOL^® 模型绘制的显示了空隙反射的一种面波图型，此时的面波长接近于产生反射峰值的面波波长。相较之下，图 5 显示了波长短得多的激励情况，虽然大部分从物体上方通过，但与物体的相互作用最小，反射也最小。

图 4.接近最优波长的反射面波（摘自参考文献 1）。

图 5. 较短波长激励产生的最小反射（摘自参考文献 1）。

在上述任一图中，都可以得到反射强度的测量值。这些测量值可以在各种波长-深度比之间进行比较，图 6 是利用 COMSOL^® 仿真导出的数据在 MATLAB^® 中绘制的。据推测，对于土地探测应用，观测峰值所在的波长，可以获得物体深度的最准确估计值。结果证实了这一推测，在深度与波长的比值大约为 0.7 处，反射最大。

图 6. 在 MATLAB^® 中绘制反射强度与波长相对物体深度的函数关系（摘自参考文献 1）。

如前所述，其余的柱坐标（距离、方位角）可使用常规方法找到，例如，通过查找脉冲的回波返回时间（测距）和发射方向聚焦脉冲使反射幅度最大（方位角）等。

如本文所述，借助 COMSOL^® 进行的仿真使研究团队能够将反射峰值的频率与埋藏物的深度联系起来。研究团队计划进一步推进这项工作，例如在大约 10 ~ 100 KHz 的频率下进行比例模型验证，以在大小适中的比例模型中获得极短的波长。在同样的背景下，研究团队基于上述比例模型，计划采用拟议方法来确定方位角和距离以完善深度。此外，团队还将进行实地测量，以测试该方法在偏离理想的实际条件下的稳健性。

扩展阅读

如果您想了解有关地震波的更多信息，可以查阅以下博客和模型：

关于作者

Masoud Zarepoor 是苏必利尔湖州立大学（Lake Superior State University，LSSU）的一名机械工程副教授。他的主要研究方向为振动、智能材料、非线性动力学和声学，获 Old Dominion 大学博士学位。他于 2016 年 8 月加入 LSSU ，一直从事振动和声学领域的教学和研究工作。他在攻读研究生期间熟悉 COMSOL Multiphysics^® 后，将其介绍给了 LSSU 工程专业的学生。LSSU 工程的专业学生将 COMSOL^® 广泛用于他们的研究和课程中，包括声学研究、结构和模态分析以及 CFD 仿真。

参考文献

D. Baumann et al., “Buried Object Localization by Spectral Analysis of Surface Wave Reflections”, 186^th Meeting of the Acoustical Society of America and the Canadian Acoustical Association, Ottawa, May 2024, paper 4pPA5; https://pubs.aip.org/asa/poma/article/54/1/045002/3308041/Buried-object-localization-by-spectral-analysis-of

MATLAB^® 是 MathWorks, Inc. 的注册商标

为什么声音在夜间传播得更远

Takumi Yoshida — Tue, 28 Jan 2025 09:22:55 +0000

当我还是一名高中生的时候，我花了很多时间练习吹奏小号。每当夜幕降临太阳落山时，我都能听到我吹出的音符在约 500 米以外的一栋教学楼里回荡。那时，我常常想，为什么只有在日落之后才能听到那些遥远的回声？这篇博客，我们将描述这一有趣的现象，并使用 COMSOL Multiphysics^® 软件及其特有的射线追踪方法对其进行模拟。

温度梯度引起的声音折射

后来我才知道，造成这种声音现象的原因是大气中温度分布的变化。温度通常随海拔高度的增加而降低。在这个示例中，由于声速与温度相关，空气中的声速随着高度的上升变得越来越慢。例如，空气中的声速可以用以下理想气体模型很好地描述。

c_0=\sqrt{\frac{\gamma R_{\rm{const}}T}{M_{\rm{n}}}}

式中，, , 和分别代表比热容比、普适气体常数、温度和摩尔质量。理想气体模型假定空气是干燥的，但一般来说，空气中的声速也取决于相对湿度。例如，校准耦合器模型就是潮湿空气中声速的典型示例。根据斯涅耳定律，当声波从声速较慢的区域入射到声速较快的区域时，会产生一个折射角小于入射角的折射波，如下图所示。

声速较慢区域和声速较快区域交界处的声音折射。

因此，在标准大气条件下的连续渐变温度场中，声音会向上折射，如下图所示。

声线在白天传播的示例。线条代表声线，背景颜色代表温度向地面逐渐升高的温度场。

在大气层中传播的声音通常会消失在天空中。然而，有时会出现逆温现象——当地表的热辐射超过太阳辐射的热量时，例如在夜间。这种反常现象会使声音向下折射，如下图所示。

声线在夜间传播的示例。

由于声音传播方向相反，在夜间可以听到更远的声音。准确模拟这种现象对于室外声学分析至关重要，因为声音传播特性的差异会极大地影响室外噪声水平和语言清晰度等因素的计算结果。

射线追踪法适用于模拟大型室外空间中的声音传播，因为它不像基于压力或波的方法那样需要精细的空间网格来解析波长。不过，在标准的射线追踪方法中，只有当光线遇到具有反射或折射条件的边界时，光线方向才会发生变化。为了计算大气中平滑的折射声线路径，必须手动设置多个边界，其中每个边界都描述了折射条件。这一过程可能会耗费大量时间，而且用户往往不清楚什么是合适的设置。在 COMSOL Multiphysics^® 中实现的基于哈密顿的射线追踪方法非常适用于室外声学分析，因为它可以准确、固有地模拟渐变折射率介质中的射线轨迹。

进一步了解 COMSOL Multiphysics^® 中使用的射线追踪算法功能，请参阅 COMSOL 博客：射线追踪算法的选择如何影响求解？这种方法也适用于模拟海洋声学问题，例如二维轴对称几何水下射线追踪教程模型中声速取决于深度的问题。

接下来，我们将使用 COMSOL 软件中的射线声学接口来计算白天和夜晚室外发生的不同的声线轨迹。

模拟长程回声

让我们使用 COMSOL Multiphysics^® 来模拟我的小号从 500 米外的教学楼发出的长程回声。为了确认回声是否只在夜间才能被探测到，我们在两种温度条件下进行了模拟。

一把小号，与本博客作者高中时练习的那把小号相似。图片由 Ballista 提供，获 CC BY-SA 4.0 许可，通过 Wikimedia Commons 共享。

我们的模拟包括下步骤：

使用 流体传热 接口计算温度场
使用 压力声学，频域 接口计算小号喇叭口的辐射指向性
使用 射线声学 接口计算声音在室外的传播

模型的几何形状和放大的源区域。

上图显示了模型的几何形状。白色开放矩形空间代表教学楼。地面的形状利用高程数据创建。

模拟假设声音从小号的喇叭口发出，演奏者位于喇叭口附近（演奏者位置用于计算脉冲响应）。图中还显示了步骤 2 中描述的放大的声源区域。

步骤 1：传热分析

第一步，设定了地面的两个温度条件：白天 25^°C，夜间 9^°C，而天空温度保持在 19^° C。将包括教学楼表面在内的其他边界设定为隔热边界条件。下图显示了白天和夜间的温度场。

白天和夜间的温度场。

在白天，可以看到垂直方向上的标准温度分布——上部较冷。在夜间，气温会出现逆转现象——上部较热。

步骤 2：压力声学分析

第二步是模拟小号喇叭口的声辐射指向性。在示例中，只考虑了喇叭口形状所产生的指向性，没有模拟任何损失。喇叭口形状被模拟为一个指数曲线形喇叭，使用 内部硬声场边界（壁） 条件，截止频率为 1200 Hz。指数曲线形喇叭的横截面半径按下式增长：

r=e^{mx}

式中

m=\frac{4\pi f_{\rm{c}}}{c}

是截止频率，是声速。空间变量用表示。请注意，上式为二维形式（假设面外方向厚度均匀）。在实际的三维指数曲线形喇叭中，横截面积随的增长而增长。

在这一步骤中，只对圆的内部区域使用有限元法（FEM）进行模拟，并使用完美匹配层（PML）进行截断。在喇叭口的入口处设置了 1 m/s² 的 法向加速度 边界条件作为激励。为了转换在步骤 1 中获得的温度场，使用了含转换参数 “Ns” 的 参数扫描 研究步骤。下列截图显示了频域研究步骤和 参数扫描 研究步骤的设置。

频域 研究步骤（左）和 参数扫描 研究步骤（右）的设置。

分别在白天（左）和夜间（右）条件下计算出的指数曲线形喇叭的辐射模式。

步骤 3：射线声学分析

第三步，分别在步骤 1 和步骤 2 中获得的温度场和喇叭口辐射指向性的基础上进行声线追踪。 COMSOL Multiphysics^® 中的射线追踪方法可以轻松计算渐变折射率介质中的脉冲响应。从 射线声学 接口的 强度计算 列表中选择 计算渐变折射率介质中的强度和功率，如下图所示。

射线声学 接口中 强度计算 的设置。

将壁节点的 混合漫反射和镜面反射 条件施加在地面和建筑物上的边界，壁节点的消失条件则指派给其他边界来模拟非反射边界。所有反射边界的镜面反射概率均设定为 0.95。假设地面很厚，使用以下近似 Wilson 阻抗模型模拟地面的声吸收。

z_{\rm{n}}=\left(\left(1+\frac{\gamma-1}{\sqrt{1+3.1\frac{j\omega\rho}{\sigma}}}\right)\left(1-\frac{1}{\sqrt{1+3.1\frac{j\omega\rho}{\sigma}}}\right)\right)^{-0.5}

式中，是地面的归一化表面阻抗。和分别表示空气密度和流动电阻率。和分别表示虚数单位和角频率。在此模拟中，流动电阻率被设定为 440 kPa s/m²。地面的法向入射吸收系数如下图所示。

地面的法向入射吸收系数。

教学楼表面的吸收系数设定为 0.05。模拟中使用了 从边界释放 功能以将喇叭口辐射指向性考虑在内。

设置从边界释放功能。

要了解 从边界释放 功能，请参考博客：小型智能扬声器的全声学室内脉冲响应。值得注意的是，这篇博客讨论了 从压力场释放 功能，它代表了在三维模型中设置声源的一种更加自动化的方法。本文使用了 从边界释放 功能进行手动设置。为了使用源计算研究的结果，将射线追踪 研究步骤和 参数扫描 研究步骤进行如下设置。

射线追踪 研究步骤（左）和 参数扫描 研究步骤（右）的设置。

射线追踪结果

下图显示了白天条件下的声线轨迹和脉冲响应。脉冲响应由设置在演奏者位置（靠近喇叭口）的接收器捕获。

白天条件下 500 Hz 的射线轨迹；射线颜色代表射线传播时间。

白天条件下演奏者位置的脉冲响应。

为了提高可视性，我们从射线轨迹图中剔除了反射次数为 0 的射线。可以看到，有些射线撞击到建筑物表面并消失在天空中，没有返回到演奏者的位置。这一现象在其他频率下也得到了证实。相应地，演奏者位置的脉冲响应没有捕获到来自建筑物的回声。下图显示了夜间条件下的声线轨迹和演奏者位置处的脉冲响应。

夜间条件下 500 Hz 的射线轨迹。

夜间条件下演奏者位置的脉冲响应。

与白天的情况不同，很多射线在夜间撞击教学楼后又返回到演奏者所在的位置。演奏者所在位置的脉冲响应还包括来自教学楼的回声。这些结果表明，教学楼在夜间接收到的声音更大。为了确认声音到底有多大，下图显示了演奏者侧教学楼表面的平均声压级 (SPL)。

演奏者侧教学楼表面的平均 SPL。

在这里，使用有限元（基于波的方法）耦合模拟的喇叭口辐射特性（在 1200 Hz 处截止）在很大程度上影响了上述声压级图的频率特性。渐变温度场中声音路径的精确模拟清楚地表明，与白天相比，声音在夜间更容易传播到远处的建筑物。在夜间条件下，建筑物表面接收到的 125 Hz-2000 Hz 的声音比白天大 5.5 分贝以上。如果声源不是小号，而是位于噪声管制地界的工厂冷凝器等设备，这种差异可能会很大。

最后，我想通过可听化来分享我的经验。在第一个示例音频中，您可以听到演奏者所在位置在白天和夜晚的声音差异。在第二个示例音频中，您将听到夜间教学楼的回声。有关可听化的更多信息，请参阅博客：使用卷积运算和可听化技术进行室内声学分析。

白天的小号声。

夜间的小号声。

调节和控制声音的重要性

这篇博客，我们解释并模拟了众所周知的现象，即声音在夜间传播得更远。文中还展示了 COMSOL Multiphysics^® 中的射线追踪算法如何用于模拟大型室外声场，以及如何适用于模拟渐变折射率介质的声音折射。噪声法规通常要求夜间的声级低于白天，因此必须考虑夜间大气中声音的折射特性。COMSOL Multiphysics^® 中的 射线声学 接口可用于准确地预测和控制室外声音，以及评估室外公共广播系统的语音清晰度。

动手尝试

想亲自动手尝试模拟文中展示的示例，请至 COMSOL 案例库中下载，其中包含有关该模型及其 MPH 文件的介绍：

获取模型

编者注：这篇博客更新于 2025 年 4 月 28 日，以包含至 COMSOL 案例库下载示例模型的链接。

地面高程数据来自 Geospatial Information Authority of Japan提供的彩色高程图。

消声效果由 The Open AIR Library 提供，获 CC BY 4.0许可。

吸声边界：局部反射与扩展反射

Takumi Yoshida — Fri, 10 Jan 2025 07:41:24 +0000

如今，无论是创建身临其境的虚拟场景、设计舒适的室内声学环境，还是优化音频体验，室内声学仿真都是设计良好声效不可或缺的一部分。声学模块是 COMSOL Multiphysics^® 软件的附加产品，包含多个适用于室内声学仿真的接口。这篇博客，我们将重点介绍吸声边界条件对室内声学仿真的重要性。

吸声性能

为了理解吸声边界条件，我们首先来讨论吸声系数。使用以下三个量来描述吸声体的吸声特性（参考文献 1）:

吸声系数，: 非反射声能与入射声能之比
比声阻抗，: 声压与吸声体表面法向粒子速度之比
复压力反射系数，: 反射声压与入射声压之比

以平面波进入多孔吸声体的理想情况来分析这些参数，具体如下图所示。

入射到多孔材料上的平面波。

这里，假定空气和多孔材料的波数分别为和。入射、反射和透射声压分别为，和。入射角、反射角和透射角分别为，和。入射声和反射声的振幅用和表示，多孔介质中的正向声波和反向声波用和表示。假定厚度为 m 的多孔吸声体为等效流体（更多信息请参见 Multiphysics Cyclopedia）。具有刚性边界的终端设置为。

根据线性声波方程，入射声、反射声和透射声在 x 方向上的粒子速度分别为，和，可表示为以下形式：

v_{\rm i}(x)=\frac{\cos{\theta}}{Z_0}p_{\rm i}(x)

v_{\rm r}(x)=-\frac{\cos{\psi}}{Z_0}p_{\rm r}(x)

v_{\rm t}(x)=\frac{B_{\rm t}\cos{\phi}}{Z_{\rm C}}\exp{(-jk_{\rm e}x\cos{\phi})}-\frac{B_{\rm b}\cos{\phi}}{Z_{\rm C}}\exp{(jk_{\rm e}x\cos{\phi})}

式中，和分别代表空气和多孔材料的特性阻抗。根据定义，反射系数可表示为:

R=\frac{p_{\rm r}(0)}{p_{\rm i}(0)}

在空气层和多孔层（x=0）的界面边界上，存在以下两个连续条件:

p_{\rm i}(0)+p_{\rm r}(0)=p_{\rm t}(0)

v_{\rm i}(0)-v_{\rm r}(0)=v_{\rm t}(0)

根据这些连续条件和费马原理，比声阻抗可由下式表示:

Z_{\rm n}=\frac{p_{\rm t}(0)}{v_{\rm t}(0)}=\frac{p_{\rm i}(0)+p_{\rm r}(0)}{v_{\rm i}(0)-v_{\rm r}(0)}=\frac{Z_0}{\cos{\theta}}\frac{1+R}{1-R}

故，

R=\frac{Z_{\rm n}\cos\theta-Z_0}{Z_{\rm n}\cos\theta+Z_0}

吸收系数可通过下式确定。

\alpha = 1-|R|^2 = 1 – |\frac{Z_{\rm n}\cos\theta-Z_0}{Z_{\rm n}\cos\theta+Z_0}|^2

因此，可以通过为边界施加三个量中的一个来模拟边界的吸声情况。同样，上述公式表明本质上与入射角相关，和是包含相位信息的复值参数，是能量参数。相位信息对于准确模拟室内模型非常重要。因此，复值参数通常是基于波的室内声学仿真的较好的输入参数。另一方面，吸声系数有利于直观地读取吸声体的性能，它是吸声测试的主要输出。随机入射吸声系数，即立体角的平均值，被视为吸声体的实际性能。

在下列公式中，我们将进一步研究多孔材料的声阻抗。

处的传输压力和速度如下:

p_{\rm t}(0)=B_{\rm t} + B_{\rm b}

v_{\rm t}(0)=\frac{(B_{\rm t} – B_{\rm b})\cos\phi}{Z_{\rm C}}

处的传输压力和速度如下:

p_{\rm t}(d)=(B_{\rm t} + B_{\rm b})\cos{(k_{\rm e}d\cos\phi)} – (B_{\rm t} – B_{\rm b})\sin{(k_{\rm e}d\cos\phi)}

v_{\rm t}(d)=\frac{(B_{\rm t} – B_{\rm b})\cos\phi}{Z_{\rm C}}\cos{(k_{\rm e}d\cos\phi)} – j\frac{(B_{\rm t} + B_{\rm b})\cos\phi}{Z_{\rm C}}\sin{(k_{\rm e}d\cos\phi)}

有了这些公式，我们就可以使用下列矩阵形式来表示入口处的参数和终端值:

\begin{bmatrix}
p_{\rm t}(0) \\
v_{\rm t}(0) \\
\end{bmatrix}=\begin{bmatrix}
\cos{(k_{\rm e}d\cos\phi)} & j\frac{Z_{\rm C}}{\cos\phi}sin{(k_{\rm e}d\cos\phi)} \\
j\frac{\cos\phi}{Z_{\rm C}}sin{(k_{\rm e}d\cos\phi)} & \cos{(k_{\rm e}d\cos\phi) \\
\end{bmatrix}
\begin{bmatrix}
p_{\rm t}(d) \\
v_{\rm t}(d) \\
\end{bmatrix}={\bm T}_{\rm F}\begin{bmatrix}
p_{\rm t}(d) \\
v_{\rm t}(d) \\
\end{bmatrix}

式中，是流体层的转移矩阵，已被广泛用于利用转移矩阵法（TMM）建立吸声和隔声模型（参考文献 2）。利用斯涅耳规则，可以将改写为下列形式:

{\bm T}_{\rm F}=\begin{bmatrix}
\cos{(k_{\rm n}d)} & jZ_{\rm C}\frac{k_{\rm e}}{k_{\rm n}}sin{(k_{\rm n}d)} \\
j\frac{1}{Z_{\rm C}}\frac{k_{\rm n}}{k_{\rm e}}sin{(k_{\rm n}d)} & \cos{(k_{\rm n}d) \\
\end{bmatrix}

式中，。在终端 ( ) 的刚性边界条件下，可以计算出多孔吸声体的比声阻抗:

Z_{\rm n}=\frac{p_{\rm t}(0)}{v_{\rm t}(0)} = \frac{\cos{k_{\rm n}d}}{j\frac{1}{Z_{\rm C}}\frac{k_{\rm n}}{k_{\rm e}}sin{(k_{\rm n}d)}}=-jZ_{\rm C}\frac{k_{\rm e}}{k_{\rm n}}\cot{(k_{\rm n}d)}

上式表明，特定声阻抗本身与角度有关。因此，要对边界上吸声进行完整仿真，应考虑吸声阻抗的角度依赖性。

局部反射和扩展反射模型

在建立边界吸声模型时，通常会采用两种吸声边界模型：局部反射模型和扩展反射模型。局部反射模型是室内声学仿真的标准模型，它使用与角度无关的阻抗（通常使用正常入射条件下的阻抗值）来描述边界的吸声特性。该模型假定吸声体表面某点的粒子速度与表面其他点的行为无关。扩展反射模型采用与角度相关的阻抗。当然，局部反射模型是近似模拟，但能准确高效地模拟声阻抗与角度关系不大的吸声体，如具有高流阻的刚性背衬多孔材料和带蜂窝芯的吸声体。扩展反射模型虽然精确，但通常需要对吸声体内部进行额外模拟。要实现准确高效的室内声学模拟，应为室内安装的吸收体选择合适的吸收边界模型。下文，我们将分别从理论和数值上来证明吸收边界类型对随机入射吸收系数的影响。

不同的表面模式如何影响吸声性能

我们计算了钢性背衬多孔吸声器和背部有空气层的隔音帘的吸声性能。将多孔材料视作厚度为 100 mm 的等效流体。采用经验 Miki 模型模拟流体特性，流阻为 13,900 Pa s/m²。由于所使用的隔音帘相对于研究频率的波长非常薄，我们使用了渗透膜模型，并将其与空气层耦合。使用渗透膜模型，可按下式计算吸声帘幕的传递阻抗:

Z_{\rm t}=(\frac{1}{R_{\rm C}}+\frac{1}{j\omega M_{\rm C}})^{-1}

式中，和分别代表流阻和表面密度分别设置为 416 Pa s/m 和 0.5 kg/m²。在理论研究中，我们使用了转移矩阵法，并将统计吸收系数作为随机入射值计算。统计吸收系数的定义如下:

\alpha_{\rm s}=\frac{\int_0^{\pi/2}\alpha(\theta)\sin\theta\cos\theta d\theta}{\int_0^{\pi/2}\sin\theta\cos\theta d\theta}

薄材料的传递矩阵表示如下:

{\bm T}_{\rm T}=\begin{bmatrix}
1 & Z_{\rm t} \\
0 & 1 \\
\end{bmatrix}

根据上述传递矩阵，可以得出含空气层的隔音帘的特定声阻抗:

Z_{\rm n} = Z_{\rm t}-jZ_{\rm 0}\cot{(kd\cos\theta)}

对于转移矩阵法，可通过代入来计算局部反射模型。

在数值研究中，我们计算了混响室吸声系数，即在混响室中测得的吸声系数。该系数值取决于测量的房间和样本大小。吸声系数早在 ISO:354 中就被作为一种标准测量程序，广泛应用于实际的室内声学设计中。

为了利用 COMSOL Multiphysics^® 有效模拟混响室吸声系数的测量，我们对带嵌入式吸声体的唯一硬质地板进行了二维模拟，如下图所示。

用于计算混响室吸声系数的嵌入式吸声器模型。

参考文献 3 中的验证研究表明，这一简化模型非常接近混响系数的测量结果。

我们使用 压力声学，边界元 接口模拟入射压力场和刚性地板，使用 压力声学，频域 接口模拟吸声体内部的压力。 多孔介质声学 功能用于模拟多孔材料。借助 声学 FEM-BEM 边界 功能，可以同时设置隔音帘的传递阻抗。对于局部反应模拟，禁用了吸声体域，将相应的法向入射声阻抗施加到吸声体表面。按照以下步骤计算混响室吸声系数:

对于入射角为的平面波，计算吸声体表面入射的和吸收的能量。
使用下式计算总吸收能量与总入射能量之比。

混响室吸声系数如下所示。

\alpha_{\rm r}=\frac{\sum_{n=1}^{N}W_{{\rm a},\theta_n}}{\sum_{n=1}^{N}W_{{\rm i},\theta_n}}

式中，是入射角数。在数值试验中，使用 背景压力场 模拟平面波入射场，和由下式定义:

W_{{\rm i},\theta_n}=\int \frac{p_0^2}{2Z_{\rm 0}}\cos\theta_n dS

W_{{\rm a},\theta_n}=\int {\bm n}\cdot {\bm I}_{\theta_n}dS

式中，是入射压强的振幅，和是吸收体表面法线矢量和入射角的声强矢量。

下图比较了多孔吸声体的随机入射吸收系数。局部反射和扩展反射之间的差异很小，但可以观察到，尤其是在高频下。因此，如上所述，对于具有高流阻和刚性终端的多孔材料来说，局部反射模型似乎是一个很好的近似。

多孔吸声体的随机入射吸收系数。

另一方面，如下图所示，隔音帘的随机入射吸收系数的比较显示出局部反射模型和扩展反射模型之间存在巨大差异。这是由于空气层具有很强的入射角度依赖性。这也符合传统规则，即对于含空气层的吸声体，扩展反射模型非常重要。

隔音帘的随机入射吸收系数。

混响室吸收系数与统计值的比较

由上文的吸收系数图中可以看出，无论采用哪种吸声体和吸收边界模型，混响室的吸收系数都大于统计值，并超过 1（理想吸收以上）。这种现象被称为“边缘效应”，是实际测量中的典型现象，它是由刚性地板到吸声体表面的能量流动引起。下图入射角为 60^° 、频率为 500 Hz 的隔音帘扩展模型即显示了这种情况。此案例中的能量流动是由样本边缘周围的声压梯度引起的：地板附近的声压由于反射声的作用而变大，而吸声体前面的声压由于吸声效应而变小。能量流动发生在样品边缘，通过增大样本面积可以减小其对吸声系数的影响。因此，ISO:354 规定了测量混响室吸声系数的样本尺寸。

入射角为 60^°，频率为 500 Hz 时的振幅和用箭头表示的声强视图。

结论

这篇博客介绍了边界吸声的理论知识，并探讨了吸声边界模型的类型如何影响吸声性能。对于室内声学仿真，COMSOL^® 中的 射线声学、压力声学、频域 和 压力声学、时域显式 物理场接口非常适用。射线声学 接口基于几何声学，无法准确模拟声波的行为。然而，我们的模拟可以表征表面吸声器的入射-角度依赖性行为，有助于提高室内声学仿真的准确性。

基于波的方法可以准确模拟边界的吸声特性。多孔介质声学 和 内部阻抗 功能可用于模拟吸声边界的扩展反射。压力声学，频域 接口可以轻松处理这些条件，因为该方法本身与频率相关。另一方面，扩展反射边界条件的时域建模非常具有挑战性，因为很难在时域中模拟吸声特性的频率依赖性。不过，我们可以在时域中使用 多孔介质声学 功能，模拟具有扩展反射的多孔吸声体。该功能的时域版本使用高效的辅助微分方程方法来考虑多孔材料的频率依赖性。因此，我们可以根据吸声体的配置灵活选择吸声边界模型。

在接下来的博客中，我们将使用时域 多孔介质声学 功能来探讨吸声边界类型的选择如何影响会议室的声学效果。

参考文献

Z. Maekawa, J. H. Rindel and P. Lord. Environmental and Architectural Acoustics. CRC Press, 2010.
J.F. Allard and N. Atalla. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials. Wiley, 2009.
T. Sakuma, S, Sakamoto and T. Otsuru. Computational Simulation in Architectural and Environmental Acoustics: Methods and Applications of Wave-Based Computation. Springer, 2014.

探讨 COMSOL Multiphysics® 中的部分分式拟合功能

René Christensen — Thu, 15 Aug 2024 08:52:07 +0000

今天,来自 Acculution ApS 的特邀博主 René Christensen 将与我们一起探讨 COMSOL Multiphysics^® 软件 6.2 版本中新增的 部分分式拟合 功能。

COMSOL Multiphysics^® 6.2 版本软件新增的 部分分式拟合 功能通过分析频率复数函数的实部和虚部,得出几个分式的总和来拟合该函数，并在相关频率范围内以一种非常严谨的方式描述系统。这些分式被称为部分分式，它们共同构成一个数值传递函数，不仅可以帮助深入理解的底层的运行机理，还能轻松变换到时域。输入值的实部和虚部通常来自 之前的 模拟，也可以来自其他软件甚至测量值。

内容简介

时频变换
传递函数
部分分式分解
部分分式拟合
实极点
复极点
重复极点
不稳定极点
非有理传递函数:时间延迟
非有理传递函数:微声学
共轭对称，负频率
结束语

时频变换

由于该功能涉及频域分析，因此简要介绍一下在频域工作的相关功能以及如何实现信号和系统的频域分析是很有意义的。

虽然信号通常会随时间变化，但是在频域对其进行分析往往更为简单。同样，对系统进行分析时，最常用的方法是将其时域特征的某些方面变换到频域。时域和频域之间的变换通常通过傅里叶变换或拉普拉斯变换以及各自的逆变换来完成，这两种变换有很多重复，这里我们将重点讨论拉普拉斯变换，因为它适用于系统分析的经典变换。已知拉普拉斯变换的单边积分形式：

\mathcal{L} \{f(t)\}(s) = F(s) = \int^{\infty}_{0} e^{-st}f(t)dt,

式中，是通过角频率和阻尼定义的复频率，即

s = i\omega + \sigma.

这种单边性使该积分适用于系统分析，因为系统可以有一个特定的“开启”时间，并且可以研究瞬态行为。此外，拉普拉斯变换将作为建立即将讨论的传递函数的主要变换。下表列出了一些重要的时域与频域的对应关系。

传递函数

许多系统可以通过包含常数和实数系数的线性微分方程来描述，形成实数和线性时不变（LTI）系统。例如，外力（输入）为，速度（输出）为的质量-弹簧-阻尼系统：

f_\textrm{ext} (t) = m \frac{dv(t)}{dt} + rv(t) + k \int^t_0 v(\tau)d\tau,

式中，是质量，是阻力，是刚度。这里，我们用速度而不是位移或加速度来表示方程，因为力和速度是功率共轭变量，就像电力系统中的电压和电流一样。

然后，在稳态假设下进行拉普拉斯变换，即假设使用复指数形式表示输入和输出的振荡和可能存在的阻尼，其中，和为实数。根据此假设，就可以对系统进行频域描述：

F(s) = msV(s) + rV(s) + \frac{kV(s)}{s}.

此处忽略了初始条件，但也可将其纳入上述方程。由于我们关注的是输入后的输出结果，因此可以使用一般的传递函数：

H(s) = \frac{Y(s)}{X(s)}.

对于当前的系统，得到以下传递函数：

H(s) = \frac {V(s)}{F(s)} = \frac {1}{r} \frac{\frac{r}{m}s}{s^2 + (\frac{r}{m})s+\frac{k}{m}}.

在工程动力学中，与线性时不变系统相关的传递函数通常是有理函数，一种只包含变量的两个单变量多项式的分数：

H(s) = \frac{b_ms^m + b_{m-1}s^{m-1}+…+b_1s+b_0}{a_ns^n+a_{n-1}s^{n-1}+…+a_1s+a_0}.

也可以用分式形式的零点和极点表示：

H(s) = K \frac{(s-z_m)(s-z_{m-1})…(s-z_2)(s-z_1)}{(s-p_n)(s-p_{n-1})…(s-p_2)(s-p_1)},

其中

K = \frac{b_m}{a_n}.

有理传递函数的一个显著特点是它们的阶数，也就是此处分母中的最高阶数，它可由指数直接获得。另一个特点是它的正当性。有三种类型需要考虑。一类称为真分式，即分母的阶数大于或等于分子的阶数，。另一类是子集，称为严格真分式，其极点数（严格地）高于零点数，即。第三类是假分式，即。对于最后一种情况，应考虑潜在的稳定性和因果性问题，但真分式还会受到是对特定传递函数还是其逆函数进行分析的影响。

对于质量–弹簧–阻尼系统而言，传递函数属于带通滤波器的范畴，这是合理的，因为在特定频率下，施加的力会在速度上产生共振。带通滤波器函数的标准形式为

H_\textrm{BP}(s) = K_\textrm{BP}\frac{\frac{\omega_0}{Q}s}{s^2+\frac{\omega_0}{Q}s+ \omega^2_0},

由此得到特征角频率为：

\omega_0 = \sqrt\frac{k}{m}

和

Q = \sqrt\frac{km}{r}.

质量-弹簧-阻尼系统的阶数为 2。这也意味着分母多项式有两个相关联的根：极点。对于本文考虑的实值系统，这两个极点有三种可能：1）两个不同的实极点；2）两个重叠（重复）的实极点；或 3）两个共轭复极点。分子的根称为零点，在收敛区域（ROC）已知的情况下，零点和极点将完全可以描述相关的线性时不变实系数系统。在此，我们假设系统是因果性，因此可以通过该信息获知收敛区域。这将导致稳定系统在复平面的右半平面没有极点，同时确保存在傅里叶变换，这正是从传递函数中找到频率响应的必要条件。由于系统为实值且存在共轭对称性，因此如前所述，复极点总是成对出现。

部分分式分解

在学习传递函数和（逆）傅里叶/拉普拉斯变换时，可能会遇到部分分式分解的主题（这样做通常是为了通过表格更容易地找到逆拉普拉斯变换）。高阶传递函数可以分解成更简单的分式，由于相关系统的线性关系成立，它们的逆变换加起来就是总逆变换。当求解包含有理函数的积分时，也可能与此相关。最后，在控制理论中将高阶传递函数分解为多个低阶分式也很有意义。

现在，我们来说明将传递函数分解为部分分式的过程，其中的极点可以写成因式分解的形式。传递函数的阶数为 5，双重复极点为-5，三重复极点为 0，因此我们需要 5 个部分分式：

H(s) = \frac{s^2 +100}{s^3(s+5)^2}= \frac{A}{s} + \frac{B}{s^2} + \frac {C}{s^3} + \frac {D}{s+5} + \frac {E}{(s+5)^2}.

等式两边同乘分母，得到

s^2 +100 = As^2(s+5)^2 +Bs(s+5)^2 + C(s+5)^2 + Ds^3(s+5) + Es^3.

对比左右两边的不同阶数，得到未知数分别为 , , , , 。

利用逆拉普拉斯变换表格，我们可以求出相关系统的脉冲响应为:

h(t) = 0.52-1.6t + 2t^2 – 0.52^{-5t} – te^{-5t}.

直接对原始传递函数进行逆变换需要使用数学软件，但通过部分分式分解，至少在零点和极点数值已知的情况下，可以手动分析完成。请注意，对于假分式传递函数，可能需要进行多项式长除法，才能将原始传递函数拆分为渐近值和后续分式。

通过 部分分式拟合（PFF）功能，我们可以充分利用时间与频率的关系，在瞬态声学中使用随频率变化的阻抗。

部分分式拟合

虽然我们通常无法为模拟的多物理场问题找到解析的传递函数，但可以找到输出与输入之间的比值，并将其作为表格中的复值。这些比值可以是模拟的输出，也可以是导入的测量值。现在，如果有办法由表格中的数值建立传递函数，就能深入理解系统，而直接从数值本身是很难理解的。还可以解析逆傅里叶变换来形成脉冲响应，不必进行如逆快速傅里叶变换等研究。最后，用零点和极点而不是大量的表格数据来描述系统，可以在保留系统的所有特性的同时使系统更加准确，至少在所选的表格值频率范围内是这样。这基本上就是 COMSOL Multiphysics^® 中 部分分式拟合 功能可以实现的，即通过频率与复值的函数关系建立数值传递函数。

在部分分式拟合函数节点中，输入的数值来自表格，其中包含实数、虚数和频率。部分分式拟合将对这些值进行拟合，得到描述底层系统的传递函数的部分分式形式。部分分式拟合基于”改进的自适应 Antoulas–Anderson (AAA) 算法，AAA² ”（见 COMSOL Multiphysics Reference Manual），其数学形式为：

\mathrm{pff}(x) = Y_\infty + \sum_{j \in N_R} \frac {R_j}{ix-\xi_j} + \frac{1}{2} \sum_{k \in N_C} \left( \frac {Q_k}{ix-\zeta_k} + \frac{Q^\ast_k}{ix – \zeta^\ast_k} \right).

方程的第一项是与拟合系统的适应性相关的渐近值，我们可以通过示例来了解它是如何起作用的。第一个求和项是对拟合函数找到的所有实值极点求和，残差也是实值。第二个求和项是对拟合过程找到的复值极点求和，残差也是复值。可以看到，复值极点和残差预计会以复值共轭对的形式出现，其中一个复值极点是另一个的镜像。稍后我们将讨论部分分式拟合结果的共轭对称性假设如何不影响到输入数值的底层系统，因此这些系统是真实或在物理上是否可实现并没有限制。

还应注意的是，在上述表达式中，是频率，而不是详细说明传递函数基本原理时使用的角频率。此外，所有分式都是一阶的，且分子中包含常数，因此对于重复的极点，可能需要做一些工作将其重新表述为部分分式分解方法所示的形式，一般来说，分子中可能有更高的阶数。除此之外，部分分式拟合本质上是以部分分式的形式得到数值传递函数，因此掌握基本的信号处理知识非常有用，包括接下来我们使用不同的示例来探究其功能的时候。

实极点

为了解如何利用这一功能找到实极点，我们将部分分式拟合应用于已知的简单解析传递函数，来了解其运行方式和得到的结果。首先，测试部分分式拟合功能输出的一阶低通滤波器函数：

H_\textrm{LP1} = K_\textrm{DC}\frac{\omega_0}{s+\omega_0} = 5 \frac{1}{s+1}.

这里，有一个实极点，当因子（或系数）被合并到分子中时，实数残差为 5。现在，我们来看看部分分式拟合函数能否求解。已知传递函数，我们就能计算出其频率响应的实值和虚值。接下来，将这些值输入部分分式拟合。我们可以将表格值（方形标记）与拟合值（实线）绘制在一起，看看拟合效果如何。在这种情况下，拟合效果看似完美，我们不仅要看曲线，还要研究实际输出，这才有意义。

显示的部分分式拟合结果为拟合的残差和极值：

参数	值	按的比例缩放后的值
		N/A

渐近值基本为零，这正是此类有理函数的预期值。由于部分分式拟合中的是以赫兹为单位的频率，而不是以弧度/秒为单位的角频率，因此计算的极点也是正确的，这样传递函数中的极点就比通过部分分式拟合计算的极点高。由于这一缩放贯穿整个方程，因此的残差比预期的低约，因此所有值都与真分式的缩放值一致。

对另一个实极点进行研究后，其传递函数如下：

H_\textrm{LP2} = \frac{1}{(s+1)(s+2)}.

由上述传递函数可以直接看到极点，因此可以手动计算部分分式，得到

H_\textrm{LP2} (s)= \frac{1}{(s+1)(s+2)} = \frac{1}{s+1}+ \frac{-1}{s+2}.

预计在频率缩放范围内，极点得到的残差为，极点会得的到残差为。这就是我们得到的基本结果：

参数	值	按比例缩放后的值
		N/A

渐近项基本为零，如果将极点和残差乘以，并翻转它们的阶数，就能得到预期值。因此，多重实极点得到了正确处理。

复极点

另一个更接近物理系统的例子是挡板中集总扬声器驱动器的压力输出，其简单的集总电路如下图所示：

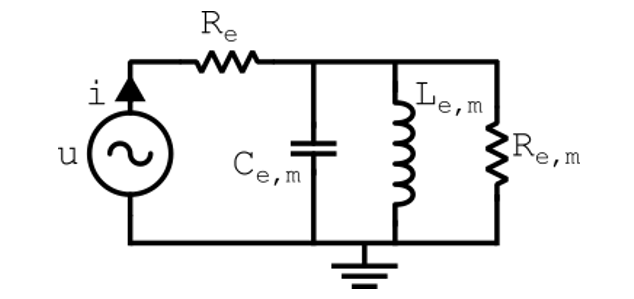
压力输出将与二阶传递函数成比例关系，可表示为

H_\textrm{Lumped}(s) = K \frac{s^2}{s^2+\frac{\omega_0}{Q_t}s+\omega^2_0},

与

\omega_0 = \frac{1}{\sqrt{L_{e,m}C_{e,m}}}

和

Q_t = \omega_0 C_{e,m} \frac{R_{e,m} R_e}{R_{e,m} + R_e}.

声压级如下图所示，既包含作为集总模型灵感的底层模拟驱动器，也包含下表中的集总参数。

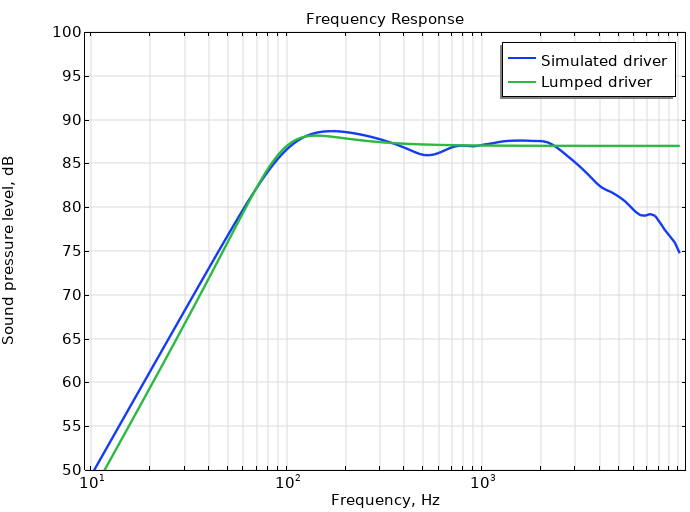
集总参数	值	单位
	5
	6
	13
	5
	4
	5
	520
	6.25
	620
	0.98722

对于给定的 Q 值，我们可以确保角频率的复极点约为，或常规频率的复极点约为。将传递函数中的值设置为 1，对函数进行简单缩放，然后运行集总模型分析。输入传递函数值的部分分式拟合，得到以下值：

参数	值

渐近项基本上等于 1，这是这个适当但并非严格适当的传递函数的预期值。有一个实极点和两个复极点。从图中可以看出，实极点不稳定，但残差很小，可以直接删除。其余复极点的值与传递函数一致，因此，您可以利用部分分式拟合的结果得到瞬态响应，也可以在底层驱动模拟数据上运行部分分式拟合，而不是在近似集总模型上运行。在这种情况下，会找到更多的极点，但方法与集总模型相同。

重复极点

传递函数可能有重复极点，比如多个极点位于平面的同一位置。正如本文部分分式分解部分所述，在对这种情况解析部分分式分解时，通常会将总和拆分为一些分母阶次大于 1 的分式，而部分分式拟合只得到一阶分式。部分分式分解法得到的值仍然是正确的，但已确定对所发现的值具有高度敏感性，因此，如果要将计算出的极值或残差导出并在其他软件中使用，则不应截断这些极值或残差。

不稳定极点

在进行部分分式拟合时，可能会发现不稳定的极点。在这种情况下，应该首先查看这些极点的残差，并与稳定极点的残差进行比较。残差可忽略不计的不稳定极点可以去除，不会影响整体拟合。如果不稳定极点对拟合精度有重大影响，则应考虑正在研究的底层系统的类型。如果系统是无源的，那么它本身就是稳定的，因此了解信号处理基础知识有助于确定在相关频率范围内表现出不稳定行为的模拟或测量问题。部分分式拟合函数提供了一个名为 翻转极点 的选项，可以将不稳定极点镜像到平面上的稳定位置。这可能会影响拟合精度，但可以通过重新绘制新的拟合图来立即评估其效果。不稳定极点通常位于低频附近，因此翻转不稳定极点可能只会对低频产生轻微影响，但高频特性不变。

一般来说，翻转不稳定极点会影响相位响应，同时保留幅值响应，但请记住，要正确解释稳定性，必须考虑因果关系假设。此外，如果大部分或所有极点都不稳定，则可能表明拟合的数据对应于一个稳定函数的逆函数，因此最好评估逆函数。

需要注意的是，应针对更多的传递函数进行有关不稳定极点和（或）重复极点的观测，以更好地掌握其功能，因此上述分析不应被视为概括了所有情况，而仅仅是作为介绍其功能的一些情况。此外，研究系统无源性的正式定义（参考文献 1 和参考文献 2）也是有意义的，本文无需进一步探讨相关条件，只需说明通常可以通过评估拟合数据中的所有实值是否为正值来进行无源性检查。

非有理传递函数：时间延迟

并非所有物理现象都能通过有理传递函数轻松描述，因此我们来看看部分分式拟合对非有理传递函数的拟合效果如何。第一个例子是秒的时间延迟，代表一个重要的传递函数，但并不是传统的有理传递函数：

H_\textrm{Delay}(s) = e^{-sT}.

传递函数是在时间延迟为 1 秒的特定频率范围内计算得出的，对于该频率范围和特定的设定容差，部分分式拟合得到的渐近项约为负 1 且只有一个实极点。

参数	值

曲线看起来拟合地非常好：

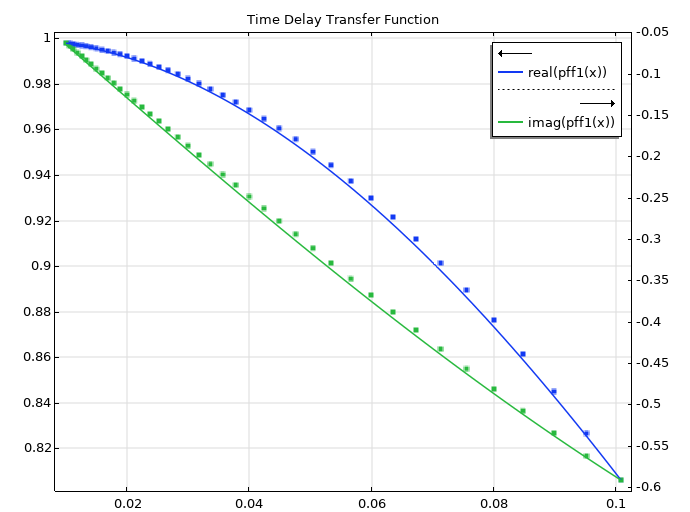
不过，我们还可以更进一步建立传递函数。根据渐近值，可以知道传递函数的类型是真分式。我们可以合并项并计算出精确的传递函数：

H_\textrm{PFF} (ix) = -1 + \frac{R_1}{ix – \xi_1} = \frac{-ix + \xi_1 + R_1}{ix – \xi_1} = -\frac{ix – (\xi_1 – R_1)}{ix – \xi_1}.

通过观察数值，我们发现残差值为极值的两倍。因此，上述表达式可以改写为

H_\textrm{PFF}(ix) = – \frac{ix – (\xi_1 + R_1)}{ix – \xi_1} = – \frac{ix – (\xi_1 – 2 \xi_1)}{ix – \xi_1} = – \frac {ix + \xi_1}{ix – \xi_1} = – \frac {ix – 0.3078}{ix + 0.3078}.

我们现在看到的是一个一阶的全通滤波器，这是合理的，因为延时器的幅值响应必须是平坦的。但还可以更进一步计算。如果分子和分母的阶数都是 1，只需找到的帕德近似（相当于双线性变换），即可得到结果：

e^{-sT} \approx – \frac{s – 2/T}{s + 2/T}.

这非常接近部分分式拟合的结果。事实上，当把上述表达式转换成格式时，，就可以得到：

e^{-ix \cdot 1} \approx \frac{ix – 1/ \pi}{ix + 1/ \pi}.

令，可以看到结果与部分分式拟合得出的结果只有很小的百分比差异。如果频率范围更大，则需要更多的极点，而且很可能会发现找到的极点代表贝塞尔多项式的根（参考文献 4）。

非有理传递函数：微声学

另一个非有理测试传递函数是关于微声学的示例。考虑一个横截面如下图所示的矩形狭缝（参考文献 5）:

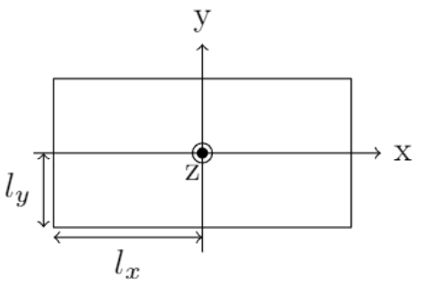
该横截面管道将在每单位长度内具有相关的声串联阻抗，以及每单位长度的声学并联导纳。这些都不能直接写成有理函数形式，但可以通过较低频率下的有源和无源元件近似，并且使用部分分式拟合能达到什么效果将非常有趣。

我们假设狭缝非常细：。这种狭缝在每单位长度内的串联阻抗如下（参考文献 5）:

Z^\prime (i\omega) = i \frac{\omega \rho_0}{S} \left( 1- \frac{\tanh\sqrt{x_v}}{\sqrt{x_v}} \right)^{-1}.

这里，是狭缝的面积；是空气的密度；，其中和是空气的黏度。将该表达式简化的一种方法是应用泰勒展开，得出如下的集总模型（参考文献 5）：

Z^\prime (i \omega) \approx R^\prime + i \omega L^\prime = \frac {3i\omega \rho_0}{x_vS} + i\omega \frac{6 \rho_0}{5S}.

低频下的串联阻抗可分为有源恒阻部分和无源恒质部分。这可以看作是一个假传递函数，但它只适用于较低的频率。因此，让我们来看看部分分式拟合能得到什么结果。我们建立了一个二维模拟，可以计算并得到特定频率范围内的阻抗，同时考虑声学和微声学效应，来揭示底层系统的特征。还必须为几何参数选择一些数值。这里，将设置为 1 cm，设置为 0.5 mm。我们可以清楚地看到，在所选几何尺寸下，黏性边界层随频率变化，在整个音频范围内厚度有大有小。

现在，我们将计算出的串联阻抗输入部分分式拟合功能。由于解析表达式中没有明确的零点或极点，无法立即猜测部分分式拟合的结果。拟合过程能很好地为残差和极点找到合适的参数，从而实现串联阻抗的拟合曲线，而且可以看到实部是如何随着频率的降低而保持不变的（泊肃叶流），这在集总模型中已经可以观察到。

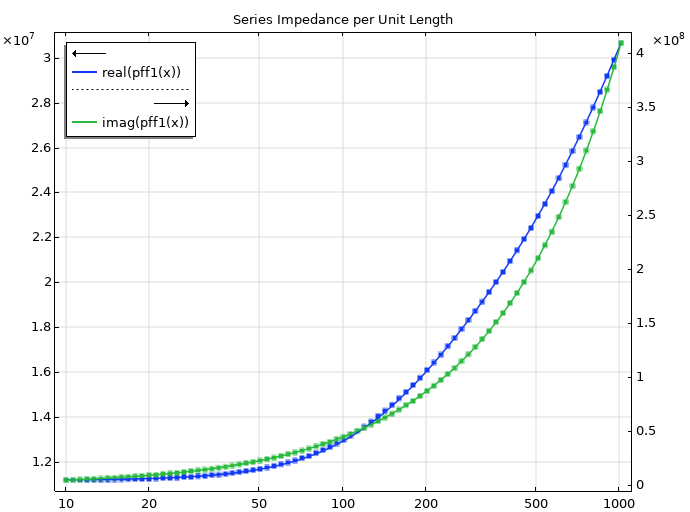
部分分式拟合得到的有限渐近值和三个实极点如下表所示:

参数	值

得知部分分式拟合在选定的频率范围内拟合时找到的极点数，就可以尝试理解这个结果了。虽然串联阻抗不是通过有理函数而是通过三角函数来描述的，仍然可以通过帕德近似值对其进行近似。由于部分分式拟合中有一个非零渐近项和三个极点，因此近似值是我们需要寻找的：

Z^\prime (s) \approx P_{3,3}(s) = \frac{\frac{23ab^2}{30030}s^3 + \frac{67ab}{910}s^2 + \frac{39a}{28}s + \frac {3a}{b}}{\frac {b^3}{18918900}s^3 + \frac{b^2}{1365}s^2 + \frac{9b}{140}s +1}.

式中，，。计算一下，基本上就能得到部分分式拟合获得的结果。

虽然由于几何结构较简单，我们可以事先通过解析方法得到单位长度的串联阻抗，但能够使用解析方法来拟合传递函数，还是非常有参考价值的。当然，我们这里的实际示例是拟合给定模拟的数值结果，而没有使用任何基本数学表达式解析。

这里选择的频率相对较低，因此研究更高频率下的拟合效果是有意义的。通过观察精确阻抗在较高频率下的表现，我们可以发现底层传递函数不是真分式。由于部分分式拟合功能在设计上会得到一个真分式的拟合传递函数，因此我们应该看到在输入频率以外的更高频率下，精确阻抗与拟合值之间会出现偏差，这就是下图所示的情况。任何拟合都只会考虑到部分分式拟合提供的频率范围，而不会保证在此范围之外的拟合效果。这也与帕德近似的渐近行为有关，但我们在此不再赘述。最后，需要指出的是，您可以研究任何相关系统的逆系统，这将改变有理传递函数的真假性，但即便如此，在拟合过程中使用的频率范围之外的值仍会出现偏差。

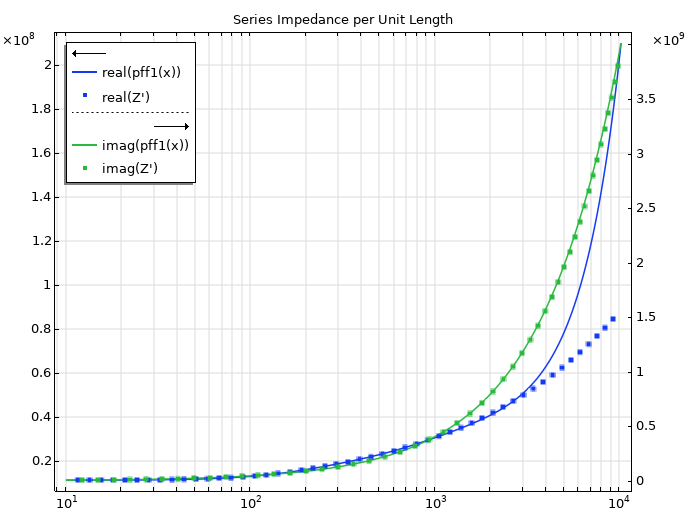
最后，可以根据部分分式拟合结果合成一个电路，如下图所示。电路计算将接近小狭缝长度的串联阻抗，其精度与相同频率范围内的部分分式拟合极值和残差相同。本篇博客不涉及合成的细节，但应该指出的是，还应以类似方式建立并联导纳来完整描述狭缝。

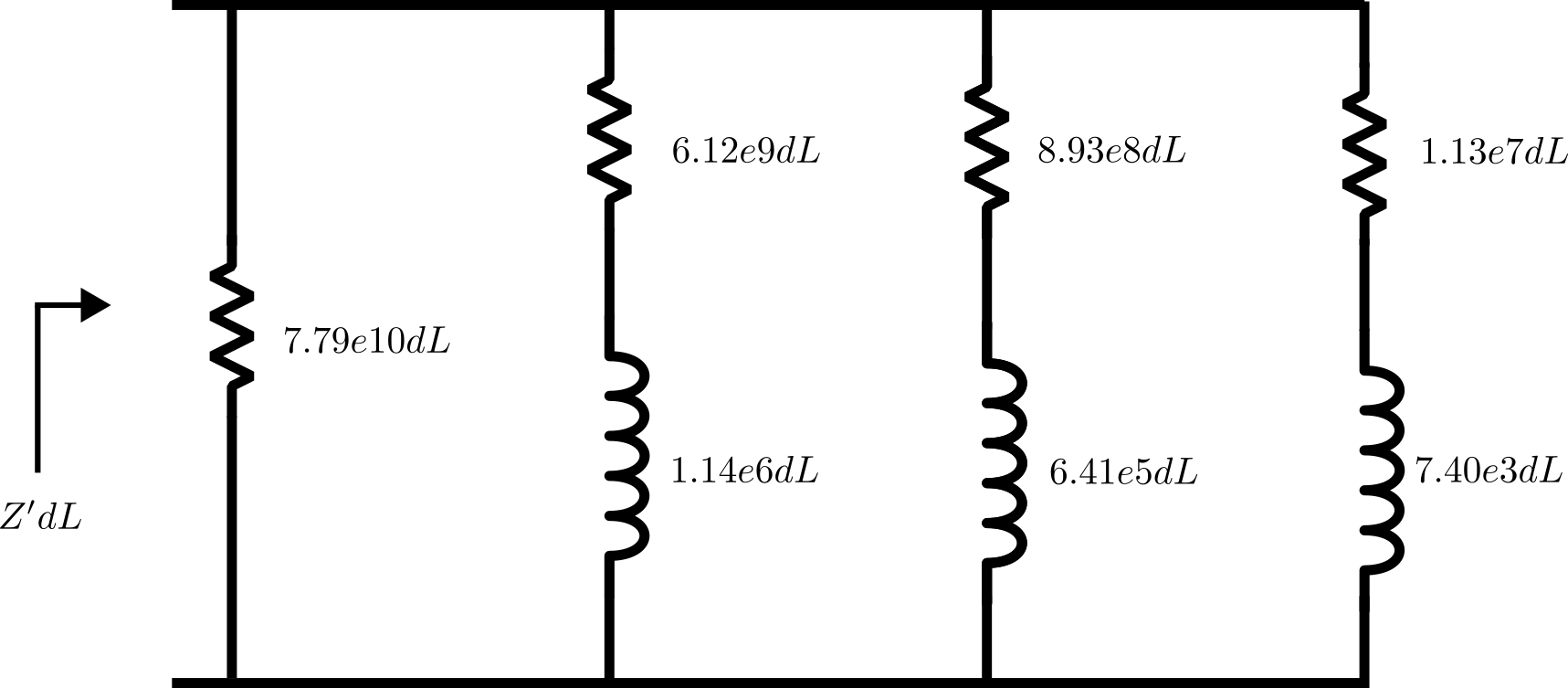
共轭对称，负频率

如前所述，部分分式拟合中的复极点将以复共轭对的形式出现。然而，原始系统必须为实数并不是一个明确的约束条件，因此它可能具有固有的共轭对称性，也可能没有。由于部分分式拟合本身具有共轭对称性假设，我们必须将输入值的频率范围限制为正频率（可能包括 0 Hz）或负频率（可能包括 0 Hz）。前者可能比后者更常见，但两种选择都有。由于初始数据可能不存在共轭对称性，因此这两个选项可能无法得到相同的拟合近似值。

结束语

本文介绍了 COMSOL Multiphysics^® 中新增的 部分分式拟合 功能在不同情况下的表现，如严格真分式、真分式和假分式的有理传递函数，以及非有理系统特性，如时间延迟、微声学效应或耦合多物理场仿真结果。该功能性能优异，可通过更改频率范围和容差选项以及直接更改残差和极点值进行手动拟合。

值得注意的是，对于某些具有实极点（在无限频率范围内）的测试传递函数，部分分式拟合有时会在其有限频率范围内得到复极点。不过，与实部相比，虚部非常小，因此很容易就能得知这在数值上仍然是合理的。请注意一种情况，即只包含实部就可以进一步简化。有时您还会看到极小的残差，因此相关极点可能并不重要，可以从部分分式拟合中删除。您还可以添加或删除极点和残差，并查看对拟合曲线的影响，这是一项非常有用的功能。

我对最新版本中的这个功能非常满意，并且这个功能可用于很多相关的应用案例。

动手尝试

想自己动手尝试 部分分式拟合 功能吗？请查看 COMSOL 案例库中的管道与耦合器测量装置的输入阻抗：使用部分分式拟合的时域模型降阶 (MOR)模型。

参考文献

B. D. O. Anderson and S. Vongpanitlerd, Network Analysis and Synthesis, New Jersey: Prentice-Hall, Inc., 1973.
Y. Miki, “Acoustical properties of porous material – Modifications of Delany-Bazley models -”, The Journal of the Acoustical Society Japan, vol. 11, no. 1, pp. 19–24, 1990.
A. V. Oppenheim and R. W. Schafer, Discrete-Time Signal Processing, New Jersey: Prentice Hall, Inc., 1989.
J. R. Martinez, “Transfer Functions of Generalized Bessel Polynomials”, IEEE Transactions On Circuits And Systems, vol. CAS-24, no. 6, 1977.
M. R. Stinson, “The propagation of plane sound waves in narrow and wide circular tubes, and generalization to uniform tubes of arbitrary cross-sectional shape”, J. Acoust. Soc. Am. 89 (2), 1991.

声阱仿真：热声流和粒子追踪

Eva Poland — Wed, 07 Aug 2024 15:26:26 +0000

声阱为各种生物医学应用提供了一种操控细胞和粒子的无接触式方法。在典型的声阱设备中，压电换能器在流体中产生压力场，从而产生能有效捕获流体中微小悬浮物的声辐射力。这篇博客，我们将深入探讨一个包括热声流和粒子追踪的声阱模型。

声阱简介

1874 年，August Kundt 首次证明了声波可以对暴露粒子施加声辐射力。自 20 世纪 90 年代以来，这一原理就已经被应用在微流体装置和片上实验室系统中，如今，商业化的声阱设备已被全球生命科学实验室和医疗机构广泛采用，用于低浓度样品的富集和纯化，细胞之间的相互作用研究、粒子分选，以及现场即时诊断的细菌、病毒或生物标记物的分离等。

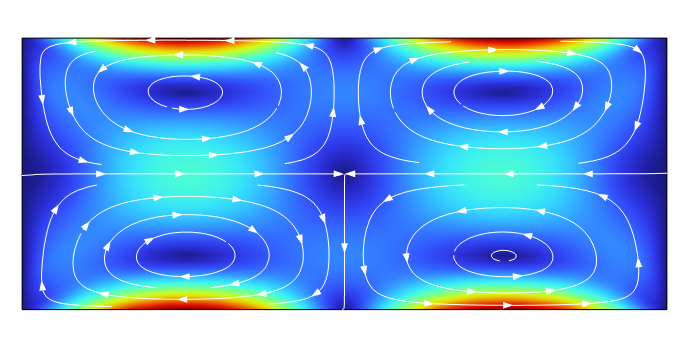
图 1 微流体通道横截面上的声流，可用于生物流体样品中对粒子进行浓缩或分离。

声阱中诱发的声波会产生声流，即在捕获位点周围形成快速移动的涡流。这种声流会对流体中的颗粒产生黏性阻力。同时，颗粒也会受到声辐射力的作用。对于大颗粒，声辐射力占主导地位，对于小颗粒，黏性阻力占主导地位。改变主导力性质的颗粒临界尺寸取决于具体的设备和颗粒的声学特性。在大多数设备中，声辐射力用于捕获或控制颗粒，因此，来自声流场的黏性阻力通常会阻止小于临界尺寸的小颗粒被声阱捕获。

了解这些信息后，让我们深入探讨如何在 COMSOL Multiphysics^® 中模拟声阱。您可以从案例库中下载文中讨论的玻璃毛细管中的声阱和热声流三维模型。

声阱仿真

示例的三维声阱几何结构如下图所示。声阱系统的几何沿两个平面对称，因此只需要计算系统的 1/4 几何：装满水（蓝色）的 1/4 玻璃毛细管（黄色）及其下方的 1/4 微型压电换能器（灰色）。实际上，相较于 0.48 mm 的高度和 2.28 mm的宽度，约 5 cm 的玻璃毛细管非常长，因此使用完美匹配层（PML）对其两端进行模拟。完美匹配层是一个可添加到几何体中的域，用于模拟所有出射波的衰减和吸收。下图中绿色显示为包含 1/2 毛细管一端的完美匹配层。在此模型中，完美匹配层在玻璃毛细管和流体中都处于激活状态。

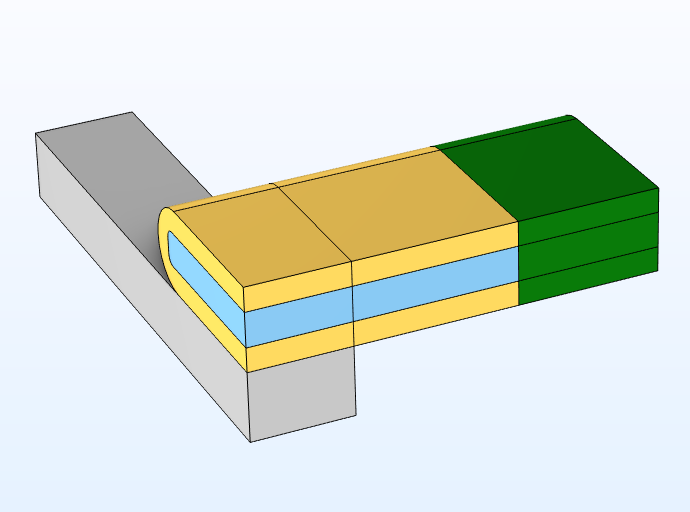
图 2 声阱的 1/4 几何结构。

声阱仿真是一个复杂的多物理场问题，涉及电磁学、固体力学、声学和流体流动等多种现象，某些情况下，还包括传热。压电换能器上的振荡电压差会引起压电材料振动，进而引起玻璃毛细管振动。这种压电效应通过耦合压电传感器域中的静电与压电传感器和玻璃毛细管的固体力学来模拟。为了模拟流体中产生的压力场，在玻璃毛细管和流体之间的边界上使用了声-结构多物理场接口，用于耦合固体力学与压力声学。

此外，压电换能器中的能量耗散会使系统升温，在玻璃毛细管和流体中产生温度梯度，进而在流体的声学特性中产生梯度，影响声流。非等温流动的多物理场耦合考虑了这种温度梯度的影响，将整个几何结构（固体和流体）的传热仿真与流体域中的蠕动流模型相结合。蠕动流和压力声学之间的耦合用于模拟声流。最后，为了验证声阱模型是否按照预期工作，使用了粒子追踪技术来确定流体中两类颗粒的轨迹，即大颗粒硅玻璃和小颗粒聚苯乙烯。

接下来，我们来看看仿真结果！

仿真结果

声场

声场使用频域计算。在频率为 3.84 MHz 的超声状态下激励系统。该频率波长的 1/2 约等于流体腔的高度。压电换能器中的电场、压电效应在压电换能器和玻璃毛细管中产生的位移场，以及由此在流体中产生的声压场如下图所示。在压电换能器上方，声场包含一个最小压力区域，称为压力节点。

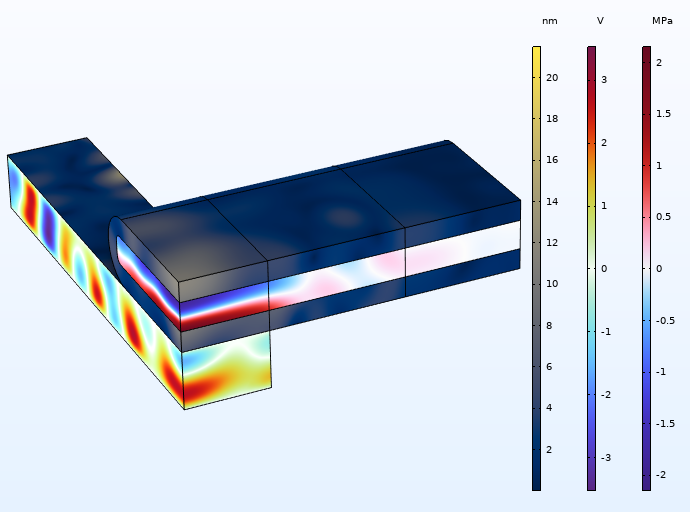
图 3 声阱中的位移场（nm）、电场和压力场。

声场中作用在颗粒上的声辐射力可以用 Gor’kov 势能来描述。图 4 显示了模型中计算的小颗粒聚苯乙烯 Gor’kov 势能。悬浮在流体中的颗粒会被推到最小 Gor’kov 势能处，从而被困在玻璃毛细管的中心。有关声辐射力的详细讨论以及如何使用 COMSOL Multiphysics^® 计算声辐射力，请查看我们之前的博客。

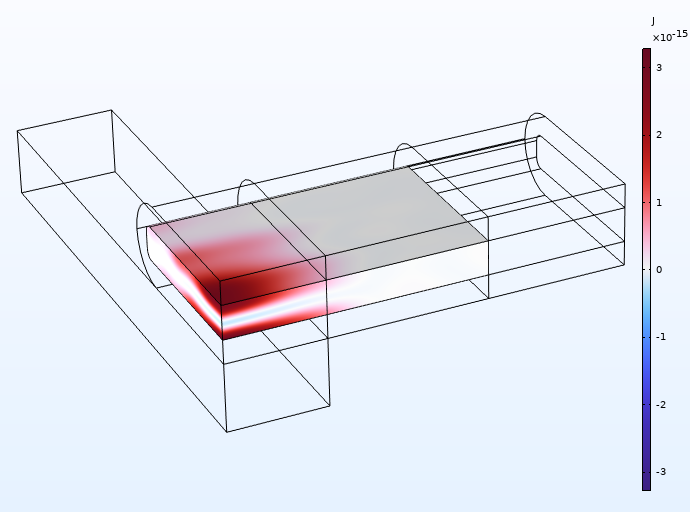
图 4 直径为 1 µm 的聚苯乙烯颗粒的 Gor’kov 势能。

热声流

声流的仿真结果如何？下图的模拟结果显示，压电换能器上方有四个涡流，这只能用温度场来解释。压电换能器的升温引起玻璃毛细管和流体产生温度梯度，从而产生流体密度梯度和可压缩性梯度。流体材料参数中的这些梯度与声学相互作用产生热声体积力，热声体积力产生声流，最终形成这种特定的声流模式。

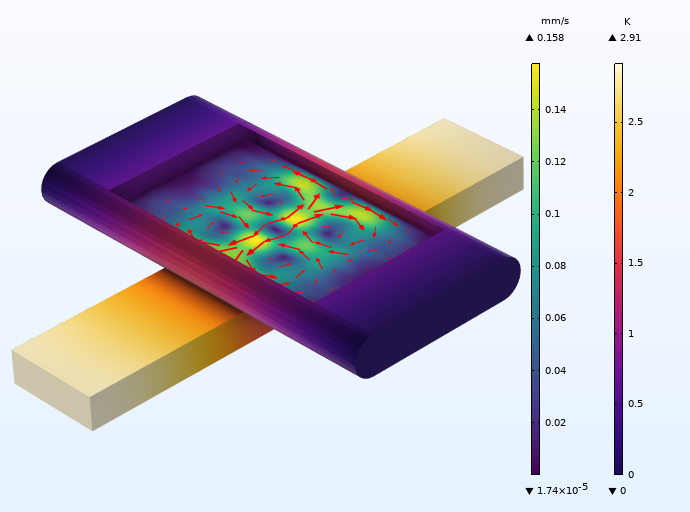
图 5 玻璃毛细管内的热声流和温度梯度。根据对称平面绘制的声阱实际几何。

粒子轨迹

通过粒子追踪，我们还可以了解具有特定性质的颗粒是否会被吸入声阱。下面的动画显示了直径为 10 µm 的大颗粒硅玻璃和直径为 1 µm 的小颗粒聚苯乙烯的计算轨迹。压电换能器上方的硅玻璃颗粒向玻璃毛细管中心移动并被困在那里，而较小的聚苯乙烯颗粒的移动则受流体流动的控制。

图6 大颗粒硅玻璃的运动轨迹。

图 7 小颗粒聚苯乙烯的运动轨迹。

动手尝试

有兴趣自己动手建立文中示例的多物理场模型吗？点击下面的按钮即可下载该模型的 MPH 文件：

获取教程模型

扩展阅读

您也可以在 COMSOL 案例库中找到一些包含声流和声阱的教程模型：

使用 COMSOL Multiphysics® 深入探究 MEMS 技术

Elsa Richardson-Bach — Wed, 17 Apr 2024 03:34:39 +0000

当你在线上会议上发表演讲，对智能设备说出语音指令，或者使用电话交谈时，你的声音很有可能是通过 MEMS 技术接收的。这种固态半导体技术经常被用于制造能产生高品质音效的现代微型扬声器。这篇博客，我们将探讨 MEMS 技术为麦克风带来的益处，制造 MEMS 麦克风所面临的挑战，以及仿真如何帮助提升这类麦克风设计过程的效率。此外，我们还将讨论由 MEMS 技术驱动的现代微型扬声器的最新进展。

MEMS 技术的现状

在麦克风中使用MEMS 技术可以提高信噪比（SNR），即所需音频信号与背景噪声之间的比值。由于 MEMS 体积小，因此能在笔记本电脑或手机等设备上添加多个麦克风。由于高信噪比以及体积小等优势， MEMS 设备具有滤波和主动降噪（ANC）功能，因此 MEMS 麦克风能够拾取清晰的语音信号，并过滤外界的环境噪声。此外，MEMS 麦克风的硅结构使其能更容易被集到成数字产品中，降低机械振动影响以及批量生产成本。

图1 一个 MEMS 麦克风模型。

由于具备上述优点 MEMS 技术越来越多地被应用到智能家居设备、手机、平板电脑、台式机和笔记本电脑，以及助听器等消费类产品的麦克风中。近年来，随着居家办公场景的增多，MEMS 麦克风的需求也在增加。

MEMS 麦克风仿真

借助仿真软件，工程师可以准确地模拟这些器件，并能放大不同的研究区域，深入探究这种微小尺度技术。对于小尺度（通常是亚毫米级）的 MEMS 麦克风，热边界层和黏性边界层的影响非常重要。边界层对系统中的摩擦损耗和热损耗都有影响，会抑制声学响应。要获得 MEMS 麦克风的正确声学响应，必须将黏性和热效应考虑在内。

随着制造技术的不断进步，开发出越来越小的设备成为可能。然而，较小的尺寸会导致较高的克努森数，使非连续效应变得非常重要。通过仿真，工程师可以测试多个不同的变量。例如，在 COMSOL 案例库中的 MEMS 麦克风模型中，可以使用边界条件来考虑 MEMS 麦克风中高克努森数的影响。

该案例中的麦克风由一个微型穿孔板 (MPP)、一个振膜和一个封闭背腔组成。对振膜表面使用了滑移条件，这样壁面的切向速度将取决于边界处的流体应力，从而在固体和流体的速度之间产生不连续性。

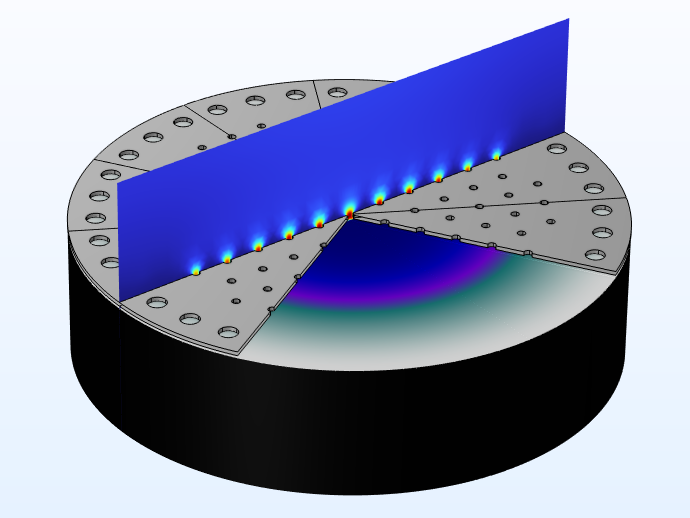
图 2 由微型穿孔板和振膜组成的 MEMS 麦克风。

接下来，我们简要介绍该模型的一些模拟结果。您可以在文末下载这个模型模拟的详细分步说明。

结果探讨

在研究的一开始，电场对振膜施加预应力，使其产生静态变形，就像拉紧吉他弦一样。然后向微型穿孔板表面施加压力，使振膜振动，并在二者之间的空间产生电信号，如图 3 所示。

图3 20 kHz 下所有域内的声压。

如图 4 所示，声速研究表明，微型穿孔板上的孔，微型穿孔板和振膜之间的挤压流动产生黏滞阻尼区域。

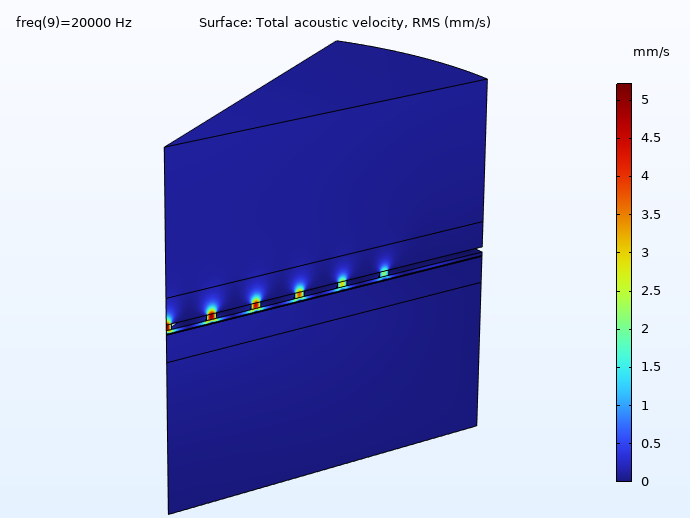
图 4 声速模拟结果。

最后，该模型分析了 MEMS 麦克风在 200 Hz 到 20 kHz 的频率响应。由于耦合电路的原因，在较低的频率下，响应曲线不再平坦，同时在较高的频率下，响应也出现下降。由于模型的长度尺度较小，机械共振位于较高频率处，因此频谱在音频范围内接近平坦。

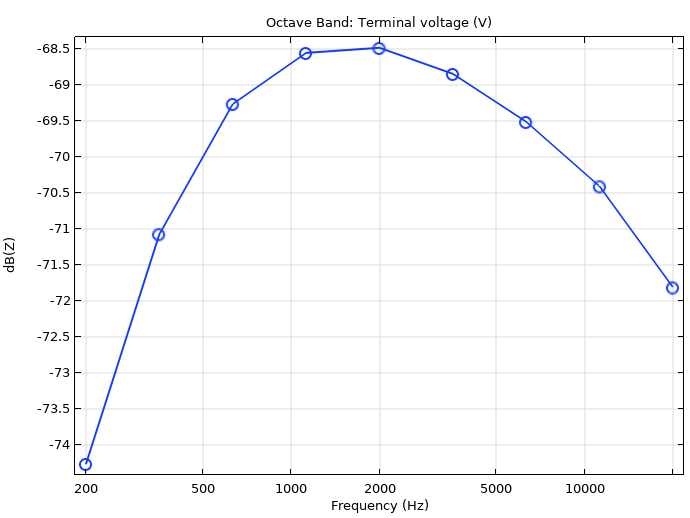
图 5 频率响应。

MEMS 麦克风常被用于日常电子设备中，在仿真技术的帮助下，其性能正不断提升。接下来，我们将探讨 MEMS 技术的一种新应用，其设计过程也能受益于仿真技术。

新的轨迹

MEMS麦克风的优点同样适用于MEMS扬声器，但直到现在这种扬声器技术还没有商业化。扬声器技术常采用由磁体、线圈和振膜组成的机械系统。几十年来，这一系统不断得到改进，但大多数扬声器都会遇到相似的设计难题，尤其是耳机设计，即磁体和线圈系统很容易出现相位不一致的情况，导致每只耳朵听到的声音不同。由于振膜本身通常不够坚硬，无法在高频时保持活塞式运动，因此可能会导致振膜在响应磁体推动时发生翘曲，使一些声音变得浑浊不清。

图 6 使用了 MEMS 驱动器的耳机。

幸运的是， MEMS 技术为这些问题提供了解决方案。由于采用了固态半导体结构，MEMS 扬声器移除了磁体，因此质量更轻、体积更小并且音量更均匀，从而消除了相位偏差。硅振膜更加坚硬，在抽气时系统可保持线性，因此声音能保持清晰、无杂音。此外，与磁体和线圈扬声器相比，MEMS 扬声器的驱动速度更快，这意味着它们能更快地启动和关闭声音，从而能更清晰地分离不同的声音。最近，一系列配备 MEMS 驱动器的无线耳机的发布标志着人类首次将 MEMS 技术应用到扬声器系统中。

MEMS 的未来

随着MEMS技术的应用，麦克风和扬声器的性能正在迅速提升。大多数麦克风已经使用了 MEMS 技术，因此能够解析出音频信号中越来越小的细微差别，之后耳机中也很可能会采用 MEMS 技术，以播放更最高质量的录音。仿真技术提供了一种深入研究微型设计的方法，以及在制作物理原型之前对设计进行精确模拟和优化，来帮助这些领域不断创新。

MEMS 为推动音频制造行业的进步开辟了许多新的通道。你下一次听音乐或进行视频通话时，可以花点时间想一想你的微型扬声器或麦克风里装的是什么，因为它可能与 MEMS 技术息息相关！

下一步

想尝试模拟 MEMS 麦克风模型吗？COMSOL 案例库中提供了相关 MPH 文件和分步说明，欢迎下载:

下载模型

扩展阅读

阅读以下资源，了解有关 MEMS 麦克风和扬声器技术的更多信息：
了解有关扬声器和声学仿真的更多信息，请访问 COMSOL 博客：
- 使用哪种耦合特征模拟扬声器驱动器？
- 如何选择 COMSOL 产品进行压电仿真？

使用卷积运算和可听化技术进行室内声学分析

Takumi Yoshida — Tue, 05 Mar 2024 08:24:51 +0000

卷积是一种有用的数学运算，被应用于信号和图像处理、统计学等多个领域。声学工程师经常使用卷积来处理声学信号，以提取所需的信息或更好地解释声音。这篇博客，我们将介绍在 COMSOL Multiphysics^® 软件中实现卷积运算的3种方法。我们将讨论使用这些方法对房间脉冲响应（IR）的低通滤波实现卷积，并通过一个室内声学可听化示例来说明。

卷积的定义和方法

从物理上讲，卷积可以给出在时域、频域或空间域中表示的两个信号之间的重叠量信息。对于时域信号，它的数学定义为

f(t)\ast g(t) = \int_{-\infty}^{\infty}f(\tau)g(t-\tau){\mathrm{d}{\tau}。

式中, 和分别表示时间变量和用于时间积分的虚拟变量，代表卷积算子。

在每个处，此方程将计算函数的原始形式与另一个函数反射和移位后的乘积的时间积分。这个运算是交换运算，即无论哪个函数被反射和移位，运算结果都保持不变。所有的移位值 () 都要进行积分，得出的卷积结果作为的函数。

这里，我们将这种积分形式称为卷积积分，它适用于处理平滑和连续函数。对于离散数据（如数字化声音信号），使用这种方法需要高要求的数值积分方案，这通常会带来巨大的计算量。为了避免这种情况，可以使用下面的离散卷积法来处理离散信号：

f(t)\ast g(t) = \sum_{\tau=-\infty}^{\infty}f(\tau)g(t-\tau)\Delta t.

式中, 是采样间隔。

通过将积分近似为离散样本的求和，离散卷积的计算速度比卷积积分更快。

如果存在两个信号的傅里叶变换，则可以使用基于卷积定理的快速傅立叶变换 (FFT) 更高效地计算离散卷积：

f(t)\ast g(t) = \mathcal{F}^{-1}\left[\mathcal{F}[f(t)]\times \mathcal{F}[g(t)]\right].

式中, 和分别是傅里叶变换算子和傅里叶逆变换算子。卷积定理利用了时域中两个函数卷积的傅里叶变换等价于信号（频域中的信号）傅里叶变换的乘积这一事实。现代实时卷积技术通常使用 FFT，因为它的计算效率更高。

房间脉冲响应的低通滤波

下面，我们将演示如何在COMSOL Multiphysics^® 中使用卷积积分、离散卷积和卷积定理来实现卷积。我们将通过一个示例来介绍这些方法的基本步骤。在这个示例中，对从小型音乐厅声学分析教学模型中获得的脉冲响应施加一个低通滤波。（声波的空气衰减就是一个常见的例子。）这些脉冲响应数据被加载并存储在一个插值函数中（本例中为插值 1）。数据图如下所示。

房间的脉冲响应图。

数据的持续时间和采样频率分别为 2s 和 44100Hz。

至于低通滤波器，我们使用的是 4 阶 Butterworth 滤波器。滤波器的传递函数定义如下：

TF(f) = \frac{2\pi \omega_c^4}{\Pi_{k=1}^{4}({j\omega-s_k})},

与

s_k=\omega_c \exp{\frac{j(2k+3)\pi}{8}},

其中，和分别代表频率和角频率。是截止频率处的角频率。是表示序列乘积的乘积算子。

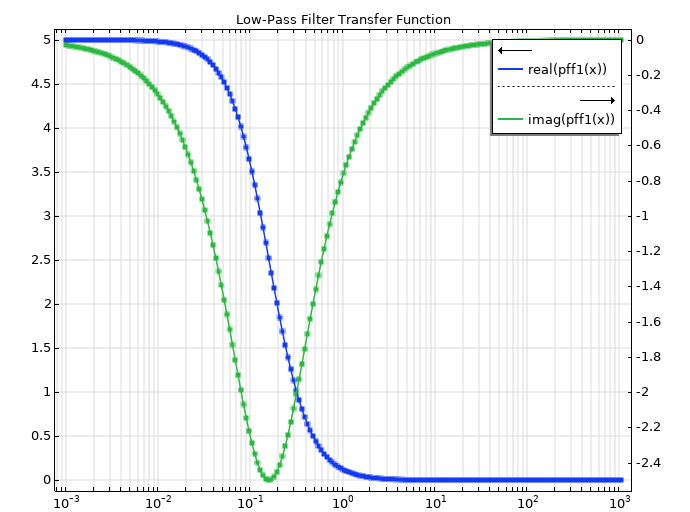
在本例中，4 阶滤波器的截止频率为 2kHz，使用 Analytic 1 函数（本例中为解析1）定义。下面的图片显示了函数的定义方式、函数的实部和虚部频率响应，以及由该函数定义的滤波器的增益特性。

4 阶 Butterworth 滤波器的传递函数是用 解析 1定义的。

传递函数实部和虚部的频率响应。

低通滤波器的增益特性。

增益特性表明，低通滤波器在截止频率 2kHz 之前具有平坦的带通（此时滤波器会将输入功率衰减一半或 3dB）。在截止频率以上，滤波器增益以每倍频程 -24dB 的速度递减。

现在，让我们来了解一下在 COMSOL Multiphysics^® 中实现卷积的 3 种方法。

方法1：直接处理卷积积分

先来看直接处理卷积积分方法。这里需要输入两个时域信号。第一个信号是房间脉冲响应信号，已经定义为插值1。第二个信号，即低通滤波器，是在频域中定义的。需要通过对信号进行反离散傅里叶变换 (IDFT) 将其转换到时域。具体步骤如下。

步骤 1

创建 Grid 1D 数据集，并将其命名为 Grid 1D_f。这将生成一个指定频率范围（-22050 Hz，22050 Hz）的频率栅格，与房间脉冲响应数据的频谱相对应。它将被用于绘制频域信号。

Grid 1D_f 数据集的设置。

步骤 2

使用一维绘图组 功能中的函数图，对低通滤波器的 Grid 1D_f 数据集进行 IDFT。在设置窗口的输出部分，从显示列表中选择离散傅里叶变换，从显示列表中选择实部，并勾选逆变换。

低通滤波器 IDFT 的设置和曲线图。

步骤 3

在表1 中添加绘图数据。

步骤 4

利用表1 中的数据定义一个插值函数（插值2）。

插值2 的设置。

现在，我们已经有 2 个可以进行卷积的时域信号。虽然定义中假定了一个无限的时间间隔，，但由于两个输入信号在此时间范围之外都设置为零，因此只需在 0–2 s 的有限时间间隔内计算积分。卷积积分的计算过程如下。

步骤 1

在几何节点定义一个间隔，使其起始值和终止值与积分区间（0–2 s）相对应。

创建间隔。

步骤 2

在间隔上定义积分算子 intop1 。

积分算子的定义。

步骤 3

使用大小等于原始房间脉冲响应数据采样间隔的均匀线网格将间隔离散化。

间隔的离散化。

步骤 4

运行瞬态研究，这样就可以在结果部分使用插值函数和 intop1 算子。

步骤 5

创建 Grid 1D 数据集，并将其命名为 Grid 1D_t。这将生成一个时间网格，用于定义 0–2 s 范围内的时间信号，采样频率为 44 100 Hz。

Grid 1D_t 数据集的设置。

步骤 6

使用 Grid 1D_t 作为源数据集，在一维绘图中进行卷积积分。

使用 dest 算子 的卷积积分表达式。

这里，IR 和 Filter_IDFT 是在 插值1 和 插值2 中定义的房间脉冲响应和低通滤波器脉冲响应的插值函数。
请注意，dest 算子 强制要求在目标点而不是源点对函数进行求值。

方法2：标准离散卷积

离散卷积广泛应于实践中。要在 COMSOL Multiphysics^® 中进行离散卷积，必须使用APP开发器。借助APP开发器中的方法编辑器，可以使用 Java 代码来创建方法，运行这些方法可以自动实现或扩展模型树中的操作。本文将举例说明使用表存储数据实现卷积的方法。

下图中显示了实现的代码和设置，下表中列出了代码中定义的变量。

用表格中存储的数据实现离散卷积的 Java方法。

名称	类型	说明
a	双（二维矩阵）	来自第一个输入表的数据
b	双（二维矩阵）	来自第二个输入表的数据
c	双（二维矩阵）	卷积结果
ndata1	整数（标量）	a 的长度
ndata2	整数（标量）	b 的长度
ndata	整数（标量）	c 的长度
dt	双（二维矩阵）	取样间隔
js	整数（标量）	求和指数的起始值
je	整数（标量）	求和指数的终止值

Java 程序中定义的变量。

代码对存储在两个输入表中的数据进行离散卷积，并将结果输出到输出表中。以下几点说明可以更好地理解代码：

第2–4行: 从第一个输入表中提取数据和数据长度
第6–8行: 从第二个输入表中提取数据和数据长度
第11–13行: 定义结果的长度，创建存储卷积结果的双精度数组，并定义采样间隔
第18–28行: 执行 for 循环，开始离散卷积，从第一个时步到最后一个时步
第30–33行: 将结果输出到标有 离散卷积结果 的输出表中

请注意，结果数据的长度是两个输入表的长度之和减 1，求和指数的起始值（js）和结束值（je）的定义是使 js 小于第二个表的长度，je 小于第一个表的长度（分别见代码中的第 22 和第 23 行）。

要运行程序，必须将两个时间信号的曲线图存储在表格中。低通滤波器 IDFT 的绘图数据存储在表1 中。对于房间脉冲响应，需要在一维绘图组 功能中使用 Grid 1D_t 数据集创建房间脉冲响应的函数图，并将图中数据复制到表2 中。

可以在添加到模型树中的方法调用 功能的设置窗口中输入表格的标记名称。所有设置完成后，点击方法调用 设置窗口中的运行按钮就可以实现离散卷积。

在方法调用 功能的 设置 窗口中输入表格标记。

方法3：基于卷积定理的离散卷积

最后一种方法是根据卷积定理进行卷积，即使用 DFT。在这种情况下，要使用房间脉冲响应的 DFT 和低通滤波器的传递函数。具体方法如下：

步骤1

在同一个一维绘图组中的两个函数图中绘制房间脉冲响应 DFT 的实部和虚部（各一个）。在设置中，从显示列表中选择 离散傅里叶变换。然后从显示列表中选择实部或虚部，分别用于绘制房间脉冲响应 DFT 的实部和虚部。复选框为默认设置。

用一维绘图表示的房间脉冲响应 DFT。

步骤 2

将房间脉冲响应DFT 的实部和虚部数据分别复制到 表 3 和表4 中。

步骤 3

分别用 表 3 和 表 4 中存储的数据定义 插值 3 和 插值 4。

步骤 4

通过计算房间脉冲响应和低通滤波器的 DFT 点乘积的 IDFT 来进行卷积。利用 Grid 1D_f 数据集，在单个函数图中完成点相乘和 IDFT。

房间脉冲响应 DFT 与低通滤波器乘积的 IDFT。选择 设置 窗口中的 逆变换 复选框可实现逆变换。

这里, real_IR 和 imag_IR 是房间脉冲响应 DFT 的实部和虚部，分别在 插值 3 和 插值 4中定义。 Butterworth 是 解析 1中定义的低通滤波器的传递函数。

请注意，卷积定理方法实现的是环形卷积，也就是说，如果网格的间隔长度不够，就会出现环形重叠。

低通滤波器的结果

下图显示了3种方法计算出的低通滤波房间脉冲响应，可以看出，3种方法的计算结果非常一致。

通过卷积积分、离散卷积和卷积定理计算出的卷积结果对比。

卷积结果范围为 0.02–0.07。

下图显示了滤波前后房间脉冲响应频谱的对比。可以确认的是，滤波后的频谱在 2 kHz 以上有所降低，而这正是低通滤波器的截止频率。这一结果证明卷积实现是成功的。

滤波前后的房间脉冲响应频谱。

可听化应用

下面我们来看一个可听化应用的例子。该示例包括房间脉冲响应和在消声室中采集的录音的卷积。假设该系统线性时间不变，可以通过脉冲响应和输入信号的卷积来计算任意输入的响应。根据这一理论，声学专家通过使用计算方法模拟的脉冲响应与消声室声音的卷积，对声场进行可听化评估。这一模拟过程被称为 可听化，包括从创建声音数据到听到声音的整个过程。示例模型（通过下一节中的按钮访问）使用前面介绍的标准离散卷积方法，对小型音乐厅模型中的小号声音进行了可听化处理。您还可以将卷积结果导出为 WAV 音频文件，以在音频或媒体播放器中播放。在下面的两个音频中，您可以比较消声室和混响室小号的声音。

小号在消声室中吹奏时的声音。

小号在小型音乐厅演奏时的声音，使用了可听化技术。

上面的示例中是单声道声音，与我们通常听到的双声道声音不同。不过，可以通过结合与头部相关的传递函数或声场再现技术，如环绕声（参考文献 1），来生成更逼真的声音。在接下来博客主题中，我们将展示这些示例。

下一步

点击下面的按钮，进入 COMSOL 案例库，进一步探索本文讨论的模型。

获取模型

延伸阅读

阅读以下博客，了解有关声学仿真中数据处理的更多信息：

参考文献

M. Vorländer, Auralization: Fundamentals of Acoustics, Modelling, Simulation, Algorithms and Acoustic Virtual Reality, Springer Science & Business Media: Berlin/Heidelberg, 2007.

消声效果由 The Open AIR Library 提供，获 CC BY 4.0 许可。

Oracle 和 Java 是 Oracle 和/或其附属机构的注册商标。

模拟热声发动机中的声能产生

Tsukasa Ishii — Thu, 15 Feb 2024 07:21:29 +0000

热声发动机通过输入的热能产生声能。与往复式发动机和燃气涡轮机等常用发动机相比，热声发动机不含活动部件，因此结构非常简单。这篇博客，我们将介绍如何使用 热黏性声学 接口模拟热声发动机的工作原理。热黏性声学接口是 COMSOL Multiphysics^® 软件中的一个功能强大的接口，用于模拟流体线性化行为。

热声发动机的工作原理

150 多年前，Pieter Rijke 教授发现并报道了一个有趣的现象，可以被看作是热声学的开创性工作。他将金属丝纱布放入一个垂直放置的玻璃圆筒管中，然后用火从底部加热纱布。熄火后，他观察到圆筒在一段时间内持续发出声音（参考文献 1）。这个装置现在被称为 Rijke管，因此有些人可能看到过它被作为解释共振现象的一个例子。然而，抛开共振不谈，声音是如何产生的呢？

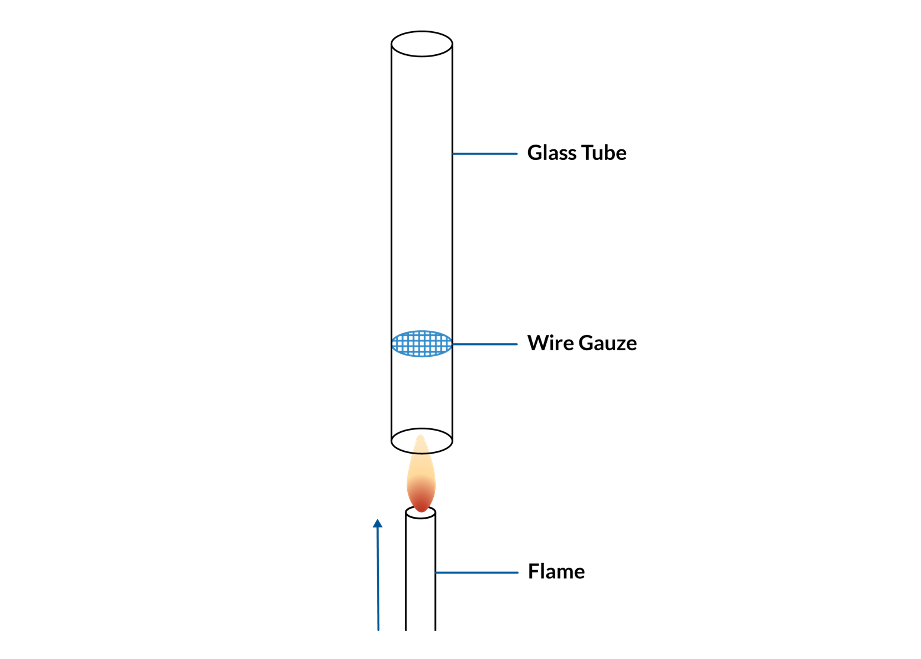
Rijke 管装置。

奥秘在于温度变化与管内流体运动之间的相互作用：加热的金属丝网引起空气自然对流，使空气在管道中稳定流动；金属丝网上方的空气温度要高于金属丝网下方的空气温度。在管内的半驻波声共振中，空气将在声周期的不同时间向两个方向流经金属丝网。当空气流过金属丝网时会被加热。由于金属丝网下方的空气比上方的空气更冷，因此当气流向上而不是向下流动时，会传递更多的热量。为了获得持续的声场，热量释放需要与压力场相位一致，这样当声压为正时，流体就会被加热。在驻波中，导致加热的速度场与压力场不同步。然而，由于金属丝网周围黏性边界层的影响，热量释放比速度场滞后。这种相位延迟导致热量释放与压力场部分同相，从而产生持续共振。如果将管横过来，对流停止，共振将不再持续。如果将管翻转过来，当声压为负时，热量传递将最大，因此声场将减弱而不是持续。

这是热能和声能之间能量转换的一个例子。事实上，整个装置展示了热声发动机的工作原理。

热声发动机有一个封闭的管状通道，声音可以在其中传播。通道内有一个热交换器，用于加热或冷却工作流体。热声发动机使用驻波或行波，而 Rijke 管仅使用驻波。由于压力和流体位移之间存在相位延迟，行波发动机有望实现比驻波发动机更好的性能。在这篇博客中，我们将主要介绍行波发动机的模型。

我们来思考一下使用行波的热声发动机的原理。要了解波是如何起作用的，请看下图中小块流体的运动。声波是纵波，因此如果高压行波从左侧传来，小块流体就会被推向右侧。同样，当来自左侧的低压波到达流体块时，它会被拉向左侧。

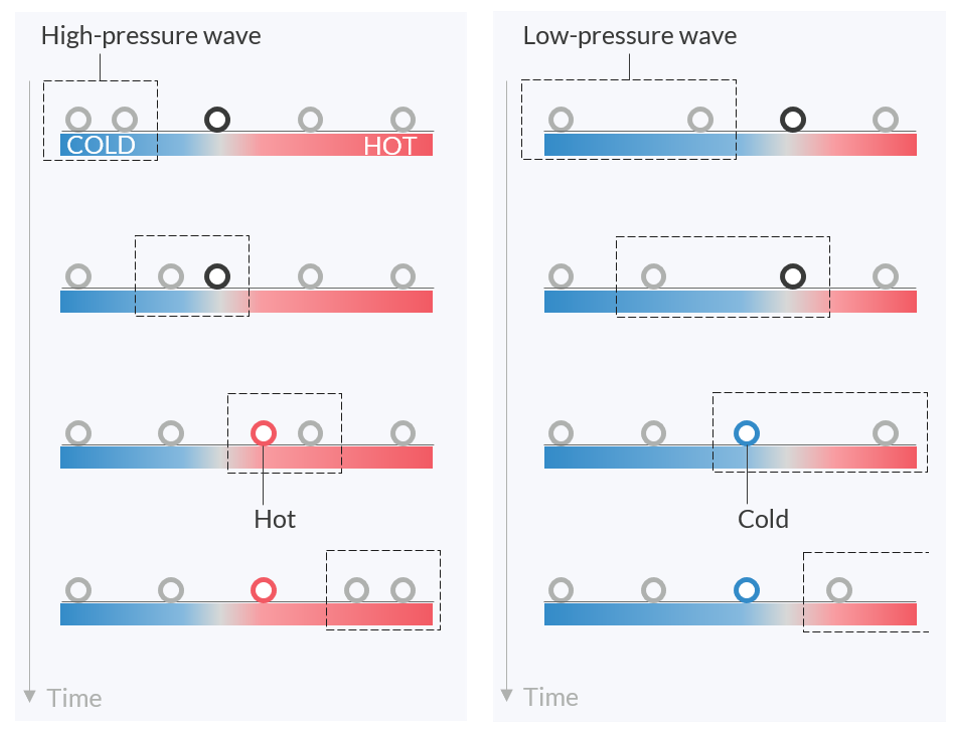
小块流体如何在来自左侧的行波下移动。用虚线框表示波的假想区域。在邻近板块有适当温度梯度的情况下，如果受到高压波的推动，流体块总是会移动到较热的区域，而如果受到低压波的牵引，流体块则会移动到较冷的区域。

假设沿波的行进路线在管中放置一块加热板。如果加热板的右端，而左端保持中等温度，那么加热板中就会出现温度梯度。当流体块向右移动时，温度梯度会加热块；当流体块向左移动时，温度梯度会吸收流体块的热量。由于流体块向右移动时压力最大，流体块的加热会将压力推至最大值。同样，流体块向左移动时吸收的热量也会降低最小气压。这些周期性的温度起伏使流体块的移动同步，最终增加了波的振幅。所有流体块像链条一样共同传递压力波，并通过热量交换为压力波增加能量。请注意，板中的温度梯度应与波的传播方向一致，否则波将会直接衰减。

如果你想知道是否存在一种与发动机循环相反的装置，答案是肯定的。这种系统被称为 热声热泵 或 热声制冷机，它可以利用声波移动热量。工作原理很简单：当高压波到达块时，块被压缩，温度随之升高，块开始向右移动的同时向邻近物体散热。相反，在低压波的作用下，块会吸收热量并向左移动。

这里给出的解释仅供参考，并不包含热声发动机的所有细节。如果想了解有关热声发动机的更多详细信息，请参阅参考文献 2。

热声仿真中的线性方程

在创建新的仿真时，考虑使用哪些方程和哪个接口是合适的始终非常重要。就我们现在介绍的仿真示例而言，使用声学模块来模拟热声振荡似乎是合理的，因为这个现象与声波有关。由于这种现象在学术领域被称为 热声学，因此 热黏性声学 接口似乎是一个不错的选择。让我们看一下这个接口的方程和功能，以验证我们的选择。

在时域分析中，热黏性声学 接口使用以下方程：

\frac{\partial \rho_{\rm t}}{\partial t}+\nabla\cdot (\rho_0 \bm{u}_{\rm t}) = 0 \\

\rho_0\frac{\partial \bm{u}_{\rm t}}{\partial t} = \nabla\cdot\bm{\sigma} \\

\rho_0C_p\left(\frac{\partial T_{\rm t}}{\partial t} + \bm{u}_{\rm t}\cdot\nabla T_0\right)-\alpha_pT_0\left(\frac{\partial p_{\rm t}}{\partial t} + \bm{u}_{\rm t}\cdot\nabla p_0\right) = \nabla\cdot(k\nabla T_{\rm t})+Q,

式中，, , , 和分别表示密度、速度、温度和压力。下标表示该值属于背景平均流，而带有下标的变量表示声学扰动。热黏性声学 接口的控制方程是根据纳维-斯托克斯方程（流体运动的精确方程）推导出来的，并基于以下假设：模拟中可以忽略每一个二阶扰动项，并且平均背景流的速度为零 ()。

必须注意被忽略的非线性因素，以及线性化方程是否涵盖我们感兴趣的现象。在热声发动机中，流体与热交换器之间的热交换由扩散项表示，声振荡引起的热传递由线性化平流项表示。由高压平流项输送的冷流体在热交换器中被加热，能量通过第三个方程递增。这些项描述了系统中重要的热传递原理，因此线性方程非常适合模拟发动机。

另外还需要注意，没有表示时变温度场与振荡速度耦合的平流项。这种耦合表示法将显示振荡引起的瞬态温度场的传输。平流项对于热泵模拟非常重要，因为平衡时的温度梯度是由振荡决定的，而不是优先的。在这种情况下，我们可以使用 非线性热黏性声学贡献 功能，它允许模型在 热黏性声学，瞬态 接口中将非线性项考虑在内。模拟非线性可能代价高，因此非线性功能仅被添加在相关域中。

在 COMSOL Multiphysics^® 中进行热声仿真

到目前为止，我们已经介绍了热声发动机的基本工作原理和相关的模拟控制方程，下面我们就开始建立模型。您可以在COMSOL 案例库中访问文中示例的模型文件。如上一节所述，我们将使用 热黏性声学 接口来建立行波热声发动机模型。由于稳态背景温度场并不均匀，因此还要使用传热接口。整个研究可分为两个步骤：背景温度场的 稳态步骤 和声场的 瞬态步骤,而不是同时使用两个接口。只需在 热黏性声学模型 节点中将传热接口的解设置为平衡温度，就可以实现耦合。

至于 热黏性声学 接口的边界条件，我们应将热交换器壁设置为等温 ()。这种条件会在压力较高时加热流体温度（由于来自较冷区域的平流，小于零），并在压力较低时冷却流体（大于零）。

示例 1：简单环

首先，我们将模拟一个由简单环组成的发动机。它的右侧通道中有一个热交换器，整个通道形成一个闭合回路。稳态温度如下图所示。热交换器下部区域的温度梯度非常醒目，但我们关注的是热交换器小间隙中的温度梯度。

简单环形发动机的平衡温度（左：整个系统；右：热交换器特写）。热交换器中狭窄通道的底部端在 493 K 的温度下被加热。

在瞬态研究步骤中，驻波被作为压力的初始条件，以便触发环路内部的振荡。随着模拟的继续，振幅不断增大，这可通过 点探针 功能获取（如下图所示）。很明显，振荡不断增强，意味着热能已转化为声能。

设置点探针 功能是为了追踪发动机内的压力。压力数据取自热交换器中的一个点，该点靠近作为初始压力分布的驻波的压力节点。

那么，发动机内的压力是怎样的呢？下面三幅图分别显示了 t = 0.281 s、0.285 s 和 0.289 s 时的压力分布。t = 0 s 时为驻波，但经过一小段时间后，压力分布开始沿顺时针方向旋转。波的传播方向与热交换器中的温度梯度相同，初始驻波的逆时针分量由于缺乏能量供应而减弱。有趣的是，逆时针方向的波的激发可以通过在模拟过程中翻转温度梯度的方向来模拟。在模型文件中，稳态研究步骤在 t = 0.3 s 时再次计算反转后的温度曲线，瞬态研究 反映了自那时起平衡温度的变化。顺时针方向的波一直保持到大约 t = 0.6 s。随后，发动机中出现了类似驻波的分布，波最终沿逆时针方向传播。

压力分布记录（左：t = 0.281 s；中：t = 0.285 s；右：t = 0.289 s）。由于前面讨论的热声效应，高压区和低压区均沿顺时针方向移动。

示例 2：带接头的环

除简单环外，我们再来看看另一种配置。下图显示了下一个具有复杂几何结构的模型示例。该几何结构模仿了参考文献 3 中的实验装置。该模型是二维的并经过简化，与参考文献中讨论的热交换器的水力直径相同。右下角的分支管道（称为接头）是为将来提取声能而添加的。与示例 1 一样，该环路用在发动机中将热能转换为声能，但是在这个示例中，部分能量可以在接头处提取。

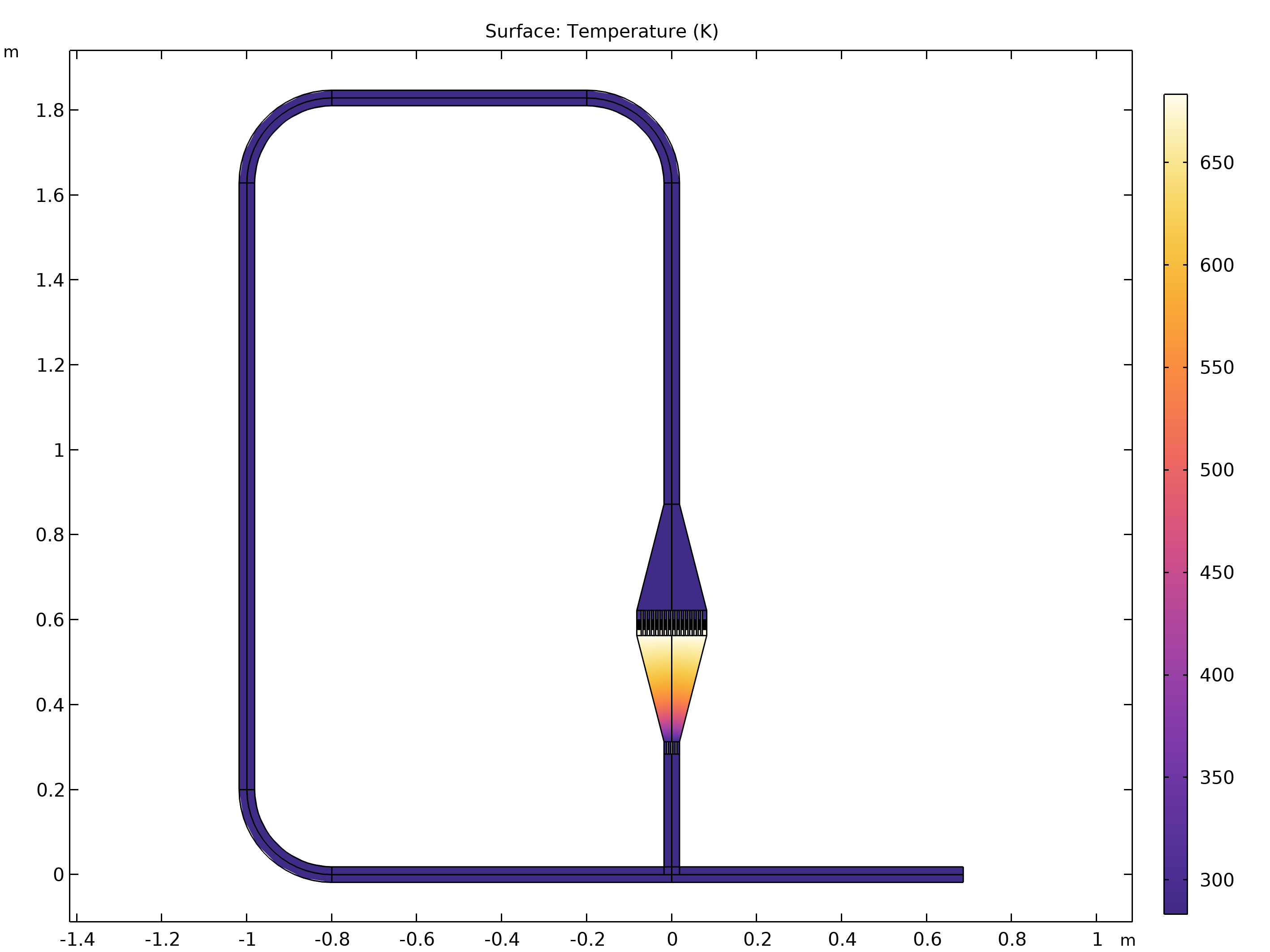
带接头的模型中的平衡温度。该几何结构模仿了参考文献 3 中的实验装置。

发动机内的瞬时压力分布如下图所示。在弧长等于 3.6 m时，压力急剧下降，这是由热交换器小间隙中的黏性阻力引起的。值得注意的是，压力的振幅与位置密切相关。这是由于模型的复杂性造成的，例如发动机中持续存在的黏性阻力和驻波分量。图中还绘制了每个位置上绝对压力的时间最大值，标记为 max(|p|)。请注意，尽管振幅看起来有点大，但该模拟假设没有湍流，任何扰动都是线性的。在对空间最大值进行无量纲化处理后，近似振幅 max(|p|) 的分布与参考文献 3 中的实验和分析数据非常吻合。

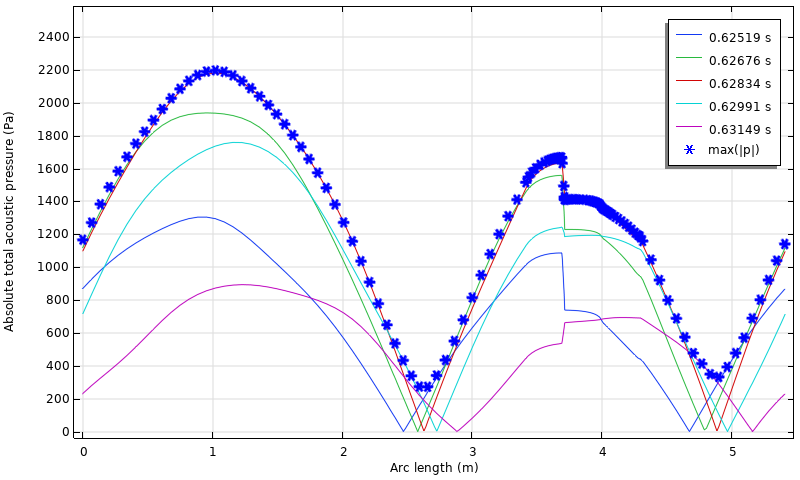
沿环的瞬时压力分布以及由状态变量计算的近似振幅 max(|p|)。

查看其他示例

自 Rijke 教授演示了热声现象以来，人们对热声学的认识有了显著提高，目前正在积极研究其在能源设备中的应用。在这篇博客中，我们介绍了如何使用 热黏性声学 接口对热声发动机进行模拟，并对发动机的有趣特性进行了可视化展示。

COMSOL 案例库包含许多跨物理学科的模型。下面是与热声学有关的两个模型：

热声发动机简化模型, 这是一个驻波热声发动机模型。有多个模型文件，可对使用 热黏性声学，瞬态 接口的线性扰动方法和 非等温流动 多物理场接口的完全非线性方法建立同一模型进行比较。后一种方法在求解纳维-斯托克斯方程时考虑了非线性因素，但代价是计算时间有所增加。
热声发动机和热泵, 这是一个驻波热泵模型。与热声发动机不同，热声热泵的仿真需要计算非线性平流项，因为温度会因热传导效应而不断降低。在模型中，非线性热黏性声学贡献 节点被添加到 热黏性声学 接口中，以考虑非线性因素。模型还使用了 热黏性声学-热扰动边界 耦合，这是 6.2 版本中的一项新功能。该耦合用于模拟振荡流体与通道中的固体板之间的热交换，因为固体温度会随着热量的泵送而不断降低。

参考文献

P.L. Rijke, “LXXI. Notice of a new method of causing a vibration of the air contained in a tube open at both ends,” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, vol. 17, no. 116, 419–422, 1859; https://doi.org/10.1080/14786445908642701
G.W. Swift, Thermoacoustics: A Unifying Perspective for Some Engines and Refrigerators, Springer, 2017; https://doi.org/10.1007/978-3-319-66933-5
M. McGaughy et al., “A Traveling Wave Thermoacoustic Engine—Design and Test,” Letters Dyn. Sys. Control, vol. 1, no. 3, July 2021; https://doi.org/10.1115/1.4049528

小型智能扬声器的完整室内声学脉冲响应仿真

Mads Herring Jensen — Fri, 07 Jul 2023 02:16:40 +0000

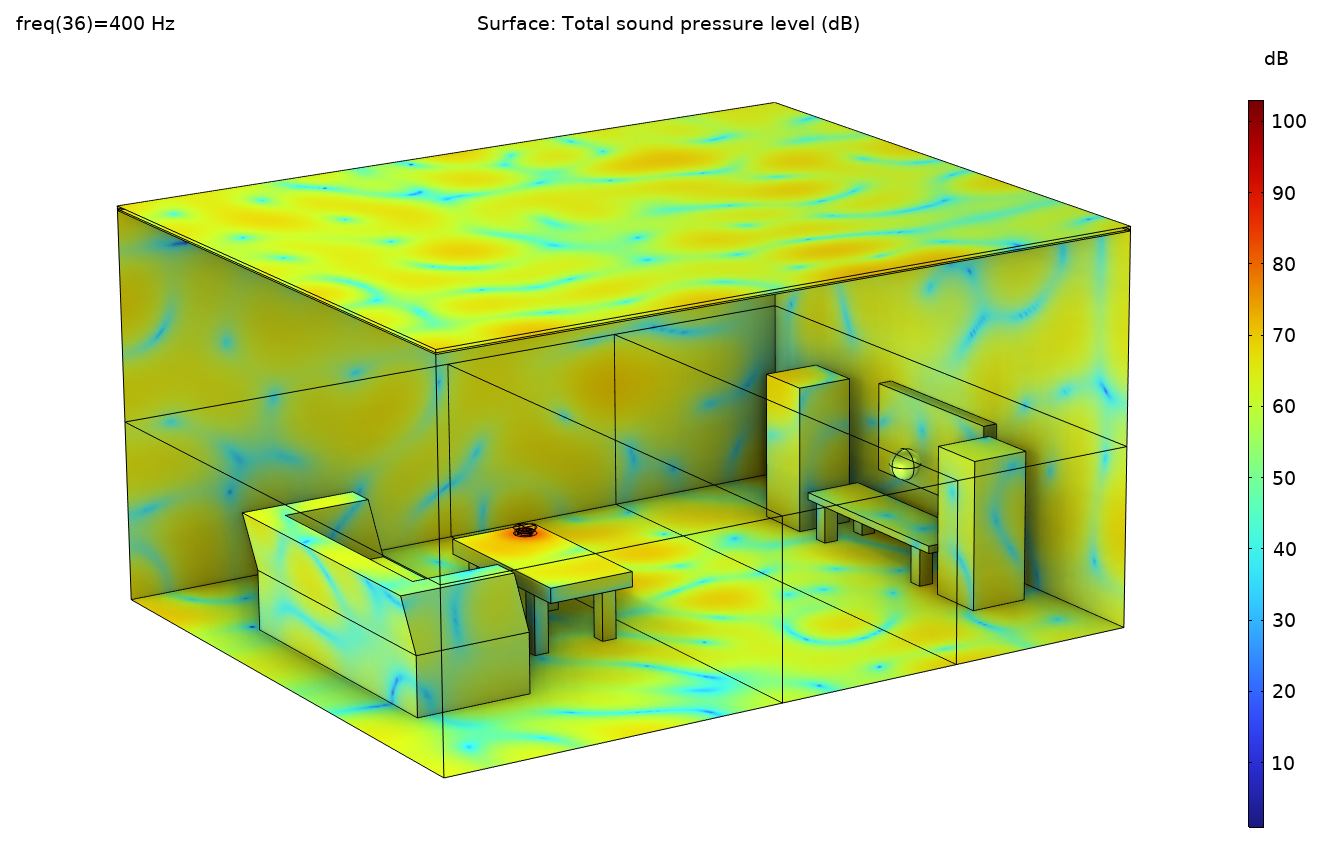
最近，我们在 COMSOL 博客中讨论了如何使用有限元-射线混合方法建立室内声学模型。本篇博客，我们将使用 COMSOL Multiphysics^® 软件中内置的有限元-射线耦合功能，对放置在一个小房间桌子上的小型智能扬声器的响应进行建模。除了使用此功能外，我们还将通过手动耦合来更详细的描述近场源。这个方法结合了详细的换能器有限元模型、全频率范围辐射特性、低频全波有限元模型和高频射线声学模型。此外，我们还模拟了随角度和频率变化的房间吊顶的吸收特性。

如果您想了解关于使用有限元-射线混合方法的博客，请点击查看：“使用混合方法建立室内声学模型”。请注意，这篇博客描述了将脉冲响应的高频和低频部分串联起来的操作，但本文并未明确讨论串联问题。

提出问题

我们以求解放置在一个小房间里的桌子上的小型智能扬声器的声学响应为例。房间的吊顶（也就是“天花板”）由一个背面为空腔的多孔材料构成。墙壁、沙发和地板也具有吸声特性。本模型只选择了一个接收器（传声器）位置，设置如下图所示。

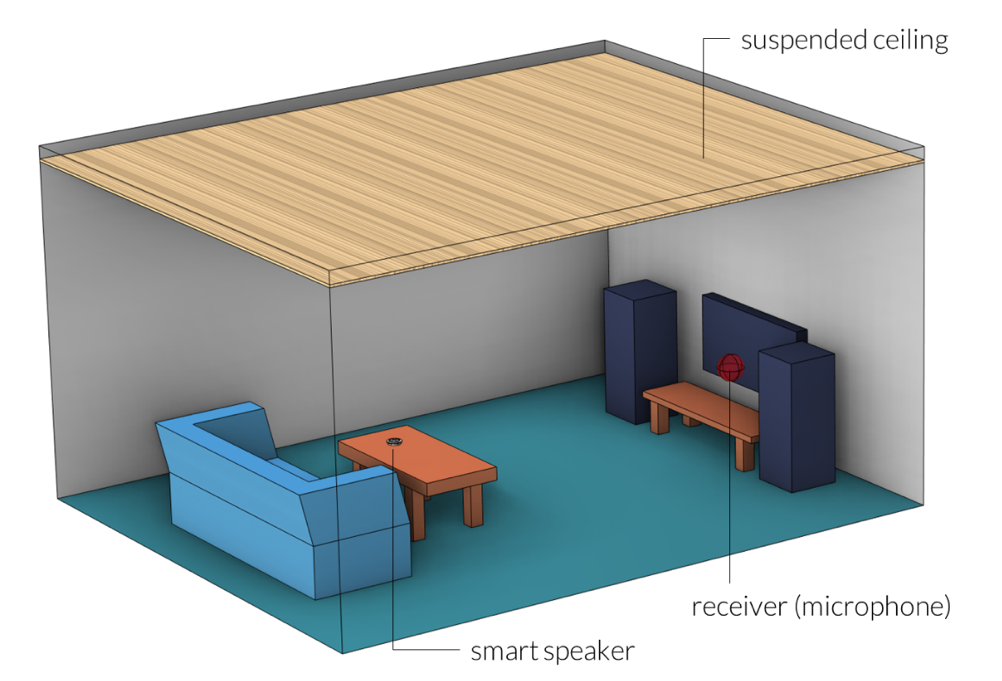
图1.问题的设置。

在当前的设置中，我们采用将压力声学与机电元件的集总表示（Thiele-Small 参数）相结合的方法来模拟小型智能扬声器。使用集总扬声器边界 功能将压力声学、频域接口 与集总电路模型耦合。有关这种建模方法的详细信息，请参阅教程模型：扬声器驱动器集总模型。

小型智能扬声器的示意图如图 2 所示。该模型包括:

前腔和背腔
扬声器振膜与集总元件模型耦合
穿孔的网格
从后部通向外部的通风口
狭窄区域和小型波导中的热黏性边界层损耗

该模型的几何结构还包括三个使用 RCL 模型模拟的麦克风，但此教程并未明确使用这些麦克风。请注意，这只是一个简化的几何体，当然也可以扩展为包含更详细的几何体和物理场的完整的多物理场模型。

图2.小型智能扬声器

图3. 1kHz 时扬声器表面声压实部。

方法组合

这里我们展示的是将最适合全波仿真的结果与高效率求解几何声学的射线追踪相结合的模型设置。在此，我们介绍了计算低频和高频所需解的必要设置。高频和低频响应的串联并不是在此模型中完成的，而是根据之前博客中介绍的模型进行的。

低频问题

对于低频系统，直接使用压力声学、频域接口 和电路接口 来解决房间和换能器的声学问题，可以通过在模型的组件 2 中设置，并在研究 2 中求解。后者用于模拟换能器机电部分。使用多孔介质声学 功能模拟吊顶。使用狭窄区域声学 功能计算扬声器内部波导结构的热黏性损耗。对于音圈和磁铁系统周围的一些损耗也很重要的区域，则使用热黏性边界层阻抗 功能求解。

在本例中，低频系统的求解频率最高可达到 1200Hz。求解的最高频率可能还会进一步提高。为了有效求解高频率，我们改用了基于移位拉普拉斯方法的迭代求解器建议。该模型可求解约 3.8e6 个自由度 (DOF)，需要约 22GB 内存。模型的求解频率从 50Hz 到 1200Hz，步长设置为 10Hz，大约需要 4 小时（具体取决于硬件配置）。需要注意的是，迭代求解器的相对容差需要设置为 1e-6，以确保有限元模型和集总参数模型的收敛性。

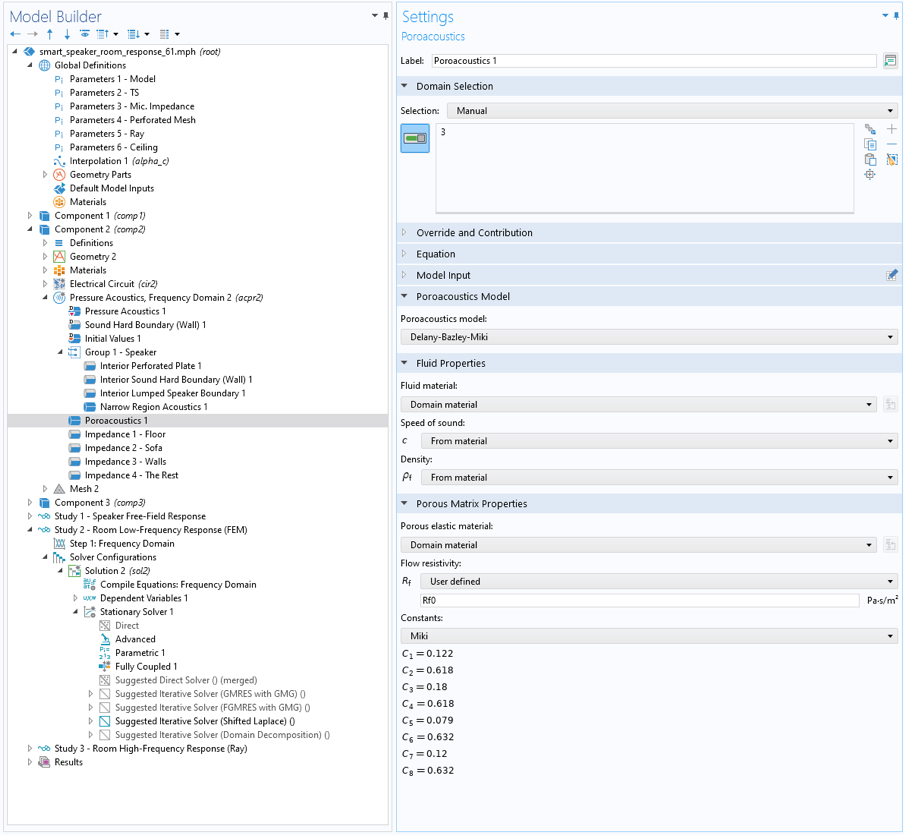
图4. COMSOL Multiphysics 的用户界面，其中的多孔介质声学功能用于对吊顶进行明确建模。

图5. 频率为 400Hz 时，房间内的声压级分布。

有关使用迭代求解器的另一个例子，请参阅汽车车厢声学-频域分析教程模型。

高频问题：两种方法

在高频范围内，使用的是射线声学接口，并与全波模拟结果相结合，用于表示扬声器的声源以及与角度和频率相关的吊顶表面阻抗。我们使用了两种声源表示方法，并进行了比较。

第一种辐射源表示法将被称为“点源释放”，从某种意义上说，它是一种经典的射线追踪辐射源。智能扬声器放置在一个立在桌子上的无限隔音板上时的辐射特性在组件 1 中建模。这个例子很好地示范了在 COMSOL Multiphysics^® 中轻松设置子模型的方法。通过根据外场释放 功能，可以直接将这些结果用于定义射线声学模拟中的点声源表示，该功能在组件3 中设置和使用，并在研究3 中求解。就电声参数和物理模型而言，智能扬声器的设置对于声源子模型和完整（低频）室内声学模型是相同的。

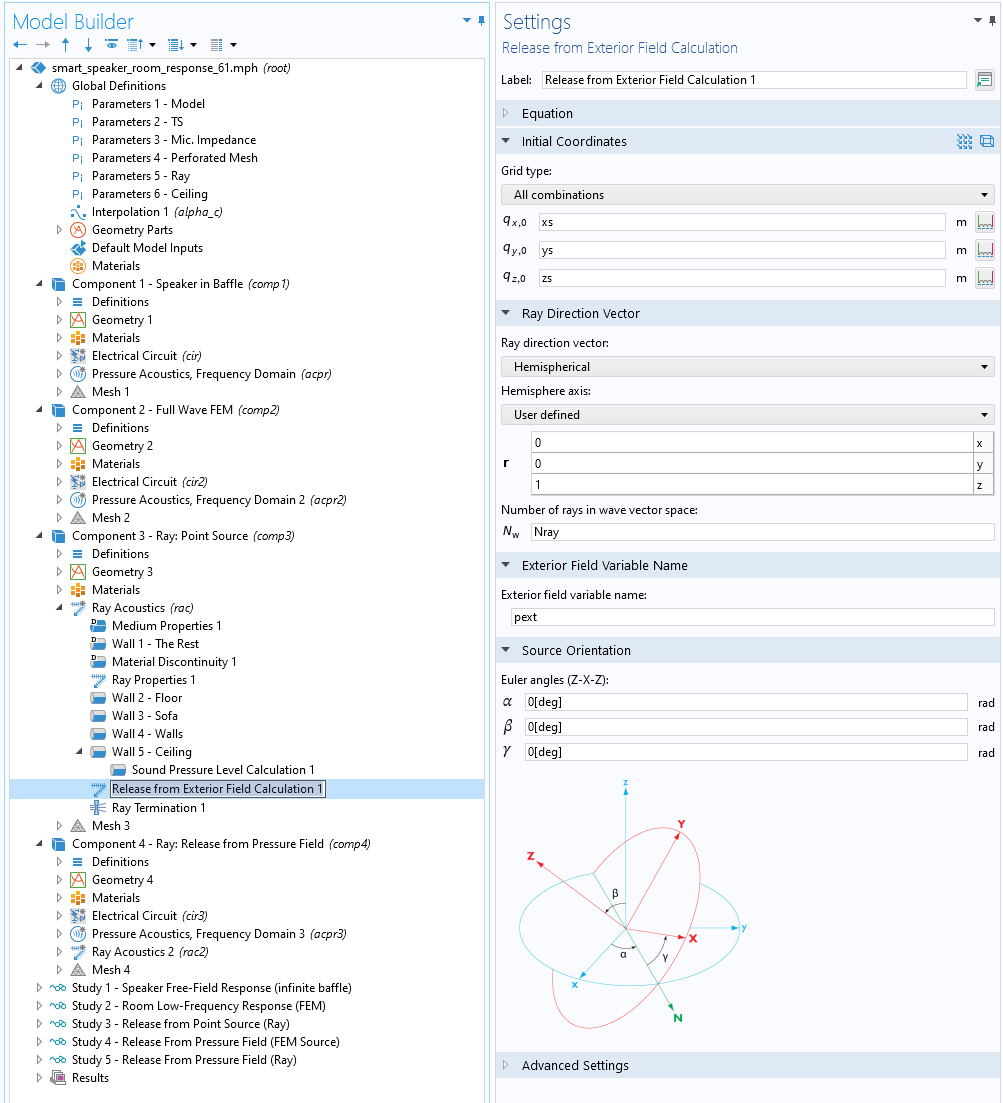
图6. COMSOL Multiphysics^® 用户界面显示了 根据外场释放功能，该功能可以自动将全波有限元模型的辐射模式与射线追踪模型结合起来。

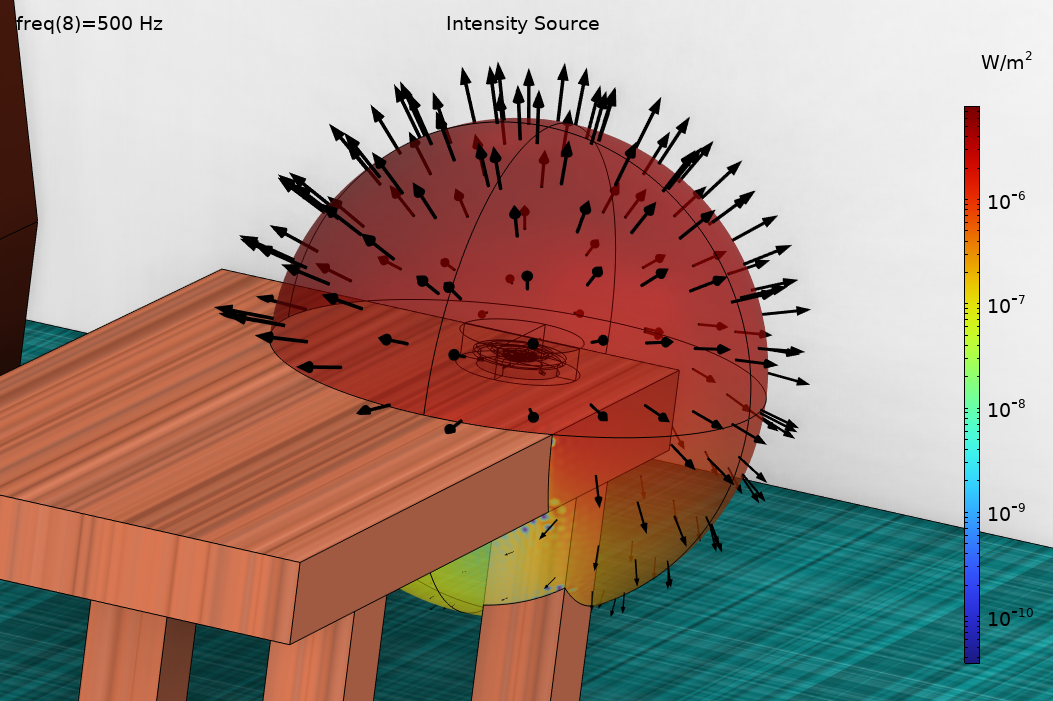
在第二种高频射线追踪方法中，源的特征不是用它的远场辐射特征（作为点源），而是用近场特征表征的，包括最靠近卓面边缘的散射细节。这将被称为 “根据外场计算释放”。在这个示例中，使用压力声学，频域接口 建立的全波有限元模型将在声源周围的球体中求解（在组件 4 中设置，在研究 4 中求解声源）。其原理是，射线从球体表面沿声学强度（“声学坡印廷矢量”）方向释放，大小为局部强度。这种设置是通过射线声学中的从边界释放功能实现的（在组件 4 中设置，在研究 5 中求解声源问题）。设置见下图 7。请注意，释放方向是归一化强度矢量，源总功率（取决于空间）是，其中是总释放面积，是表面法线。在这两种情况下，表达式都包含在 bndenv() 算子中，从而确保有限元求解可以映射到射线上。

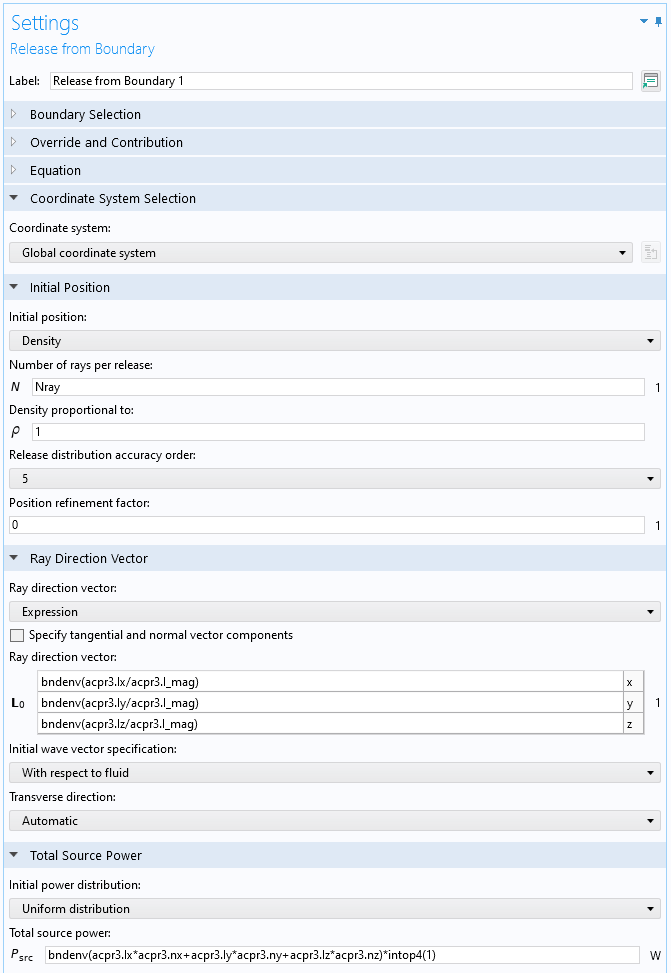
图7. 从边界释放功能的 COMSOL Multiphysics 用户界面设置。

图8. 释放球体表面的射线释放方向和强度示例。

压力场释放设置结合了全波方法（近场）和射线追踪的相关假设，这也为使用这种方法设置声源设置了一些限制。例如

当使用从边界释放射线时，射线是同时释放的。因此，应该假定从声源发出的声音会同时到达和离开释放边界的每一部分。然而，要做到这一点，就不能随意设置释放边界。
由于上一点提到的限制，源域中的内部反射就很难考虑在内。根据反射路径的不同，声音确实可以传播不同的距离，这将导致在释放边界和脉冲响应中出现不同的时间事件。
最后，在射线追踪中计算的脉冲响应不包括时间延迟（从源到释放边界的飞行时间）。COMSOL^® 软件假定释放边界处的释放时间为 0。

在这个模型中，近场球半径设置为 0.3 米。选择这个尺寸是为了防止局部全波问题太大而无法求解，同时还能显示最近的桌面边缘的影响。

请注意，这两个射线跟踪模型都包括了吊顶吸收的角度和频率相关性。这些特性是在一个单独的模型中计算得出的，如下图所示。

吊顶的特性

通过对多孔层（使用压力声学，频域接口 中的多孔声学 功能）和空腔进行建模，将吊顶的特性直接纳入模型的低频分析部分。在（高频）射线追踪模拟中，吊顶的吸收特性被包含在与频率和入射角有关的吸收系数中。吸收数据是从吊顶的子模型中提取的。该模型也可在此处下载。该模型采用了与多孔吸声体教程模型类似的方法。一般来说，使用子模型是为射线跟踪模拟获取更详细的边界（和源）条件的一个好方法。

下图显示了模型中吊顶的吸收面。该吊顶由 1cm 的多孔材料制成，流动电阻为 20,000 [Pa-s/m²]，后面是 2cm 的空腔。在射线追踪模型中，通过调用一个带有频率参数和入射角变量 rac2.wall5.thetai（标记为射线声学模型 2 和壁条件 5）的插值函数，包括了角度和频率相关性。

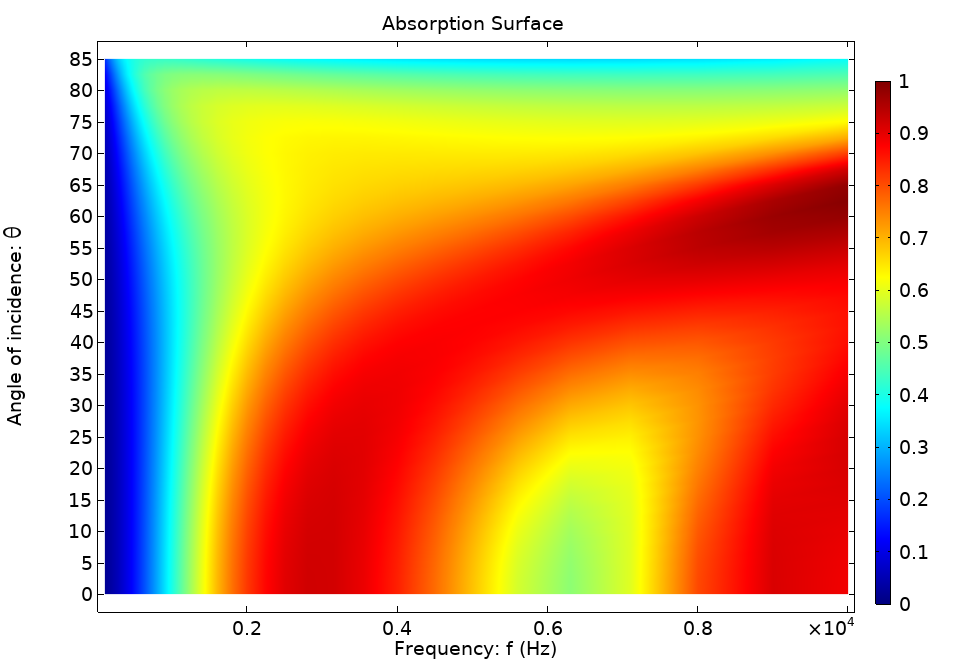
图9.吊顶的吸收系数面。

为简单起见，目前的模型只包括天花板的详细吸收数据。模型完全可以扩展到包括所有边界的角度和频率吸收数据。详细的散射数据也可以通过全波模型计算得出，如施罗德扩散器二维模型教程模型所示。

边界条件考虑

本文讨论的模型有多种用途，可以在边界条件做出各种假设。这些假设取决于重点是压力声学仿真还是射线声学仿真。让我们来详细了解一下建模注意事项和假设是如何根据仿真类型发生变化的。

首先，让我们来看看压力声学仿真的一些注意事项：

这里会模拟相位信息，因此一般最好使用与频率相关的阻抗条件。
在低频情况下，仅使用吸收系数通常并不准确。
表面的法向阻抗取决于入射角。那么，应该使用什么值呢？对于没有明确入射角的室内声学应用，使用有效入射角通常是一个不错的选择。例如，根据阻抗条件中多孔层 选项的定义，在自动设置下以 50° 入射角进行计算法向阻抗。
如有可能避免上述假设，最好像本模型中的吊顶一样，对实际吸收表面进行建模。

在射线声学仿真中，考虑使用

正态与随机入射吸收系数
随角度变化的吸收系数
散射系数

正常（和随机）入射的吸收系数、角度相关吸收系数和散射系数可以是常数，也可以是频率相关系数，但模拟选项也取决于可用的数据。

此外，对于射线声学仿真，如果壁的吸声在一个倍频程内变化很大，可考虑使用更窄的频带表示，如 1/3 倍频程或甚至 1/6 倍频程频带。

结果

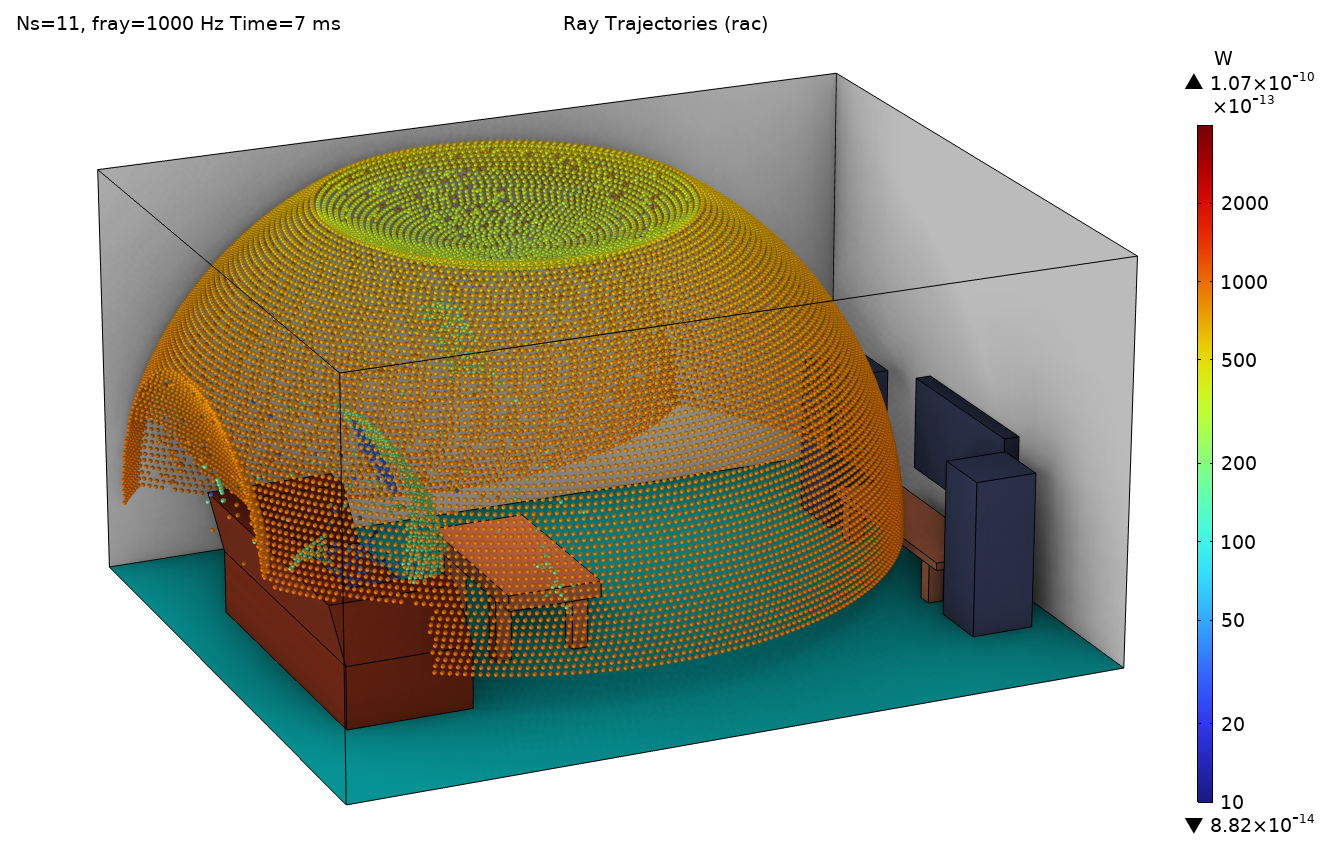
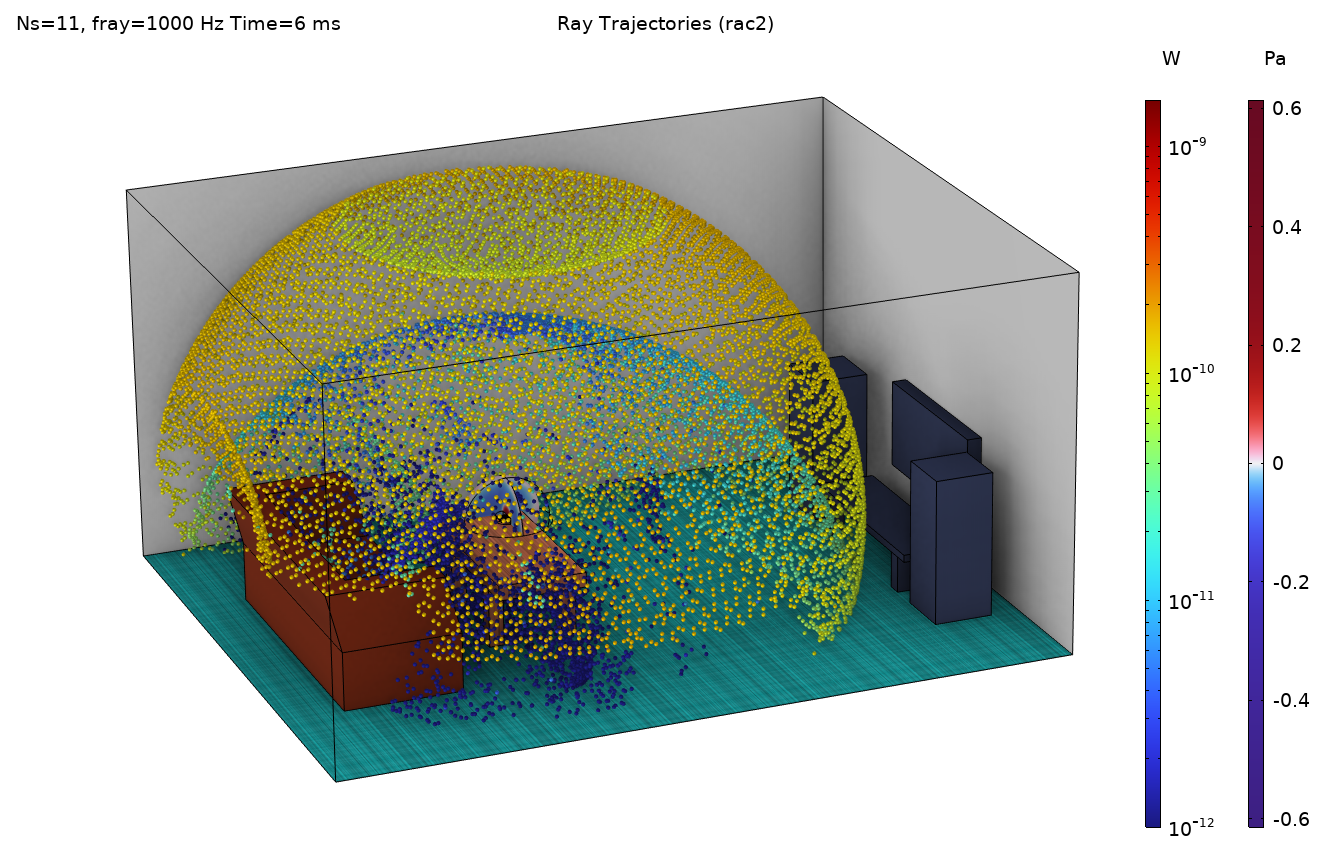
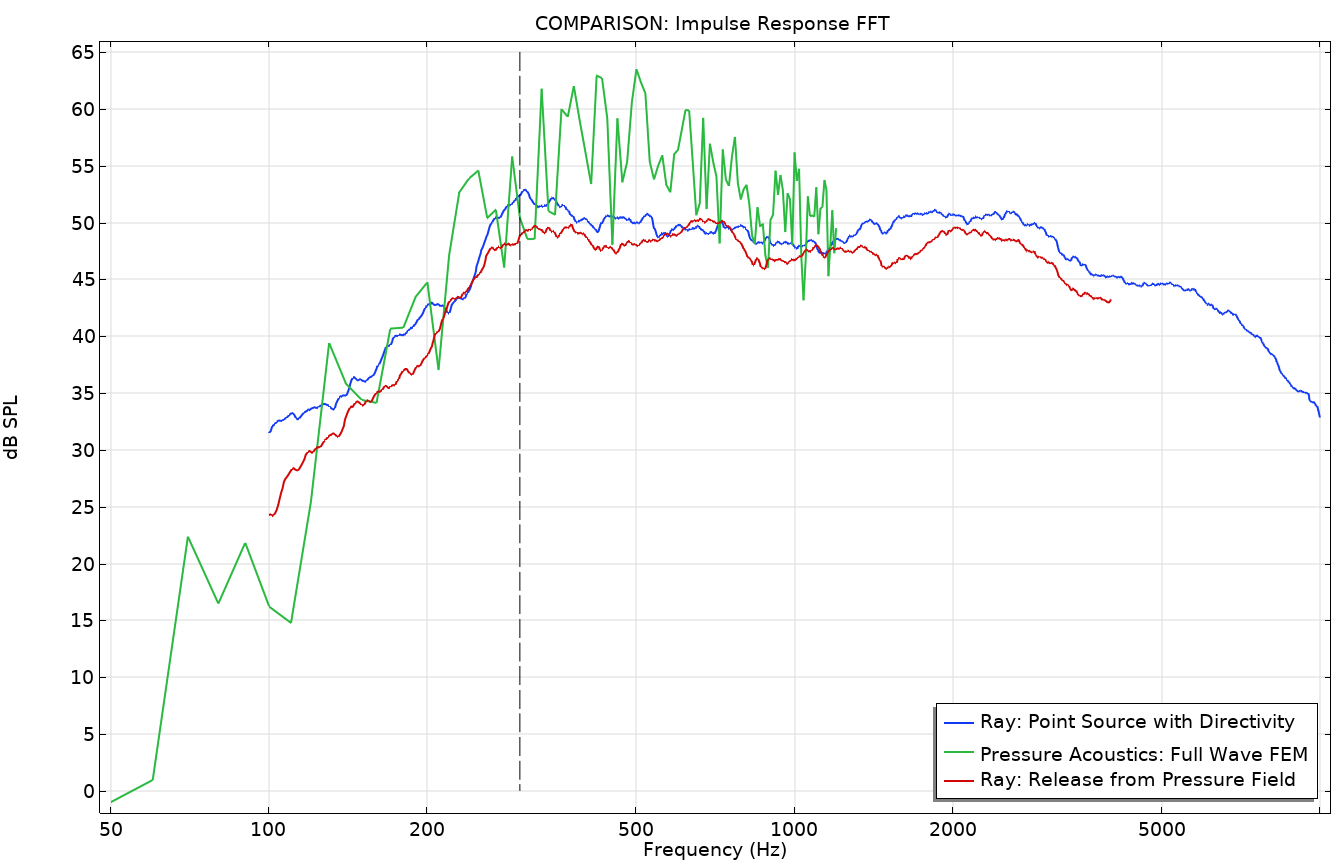
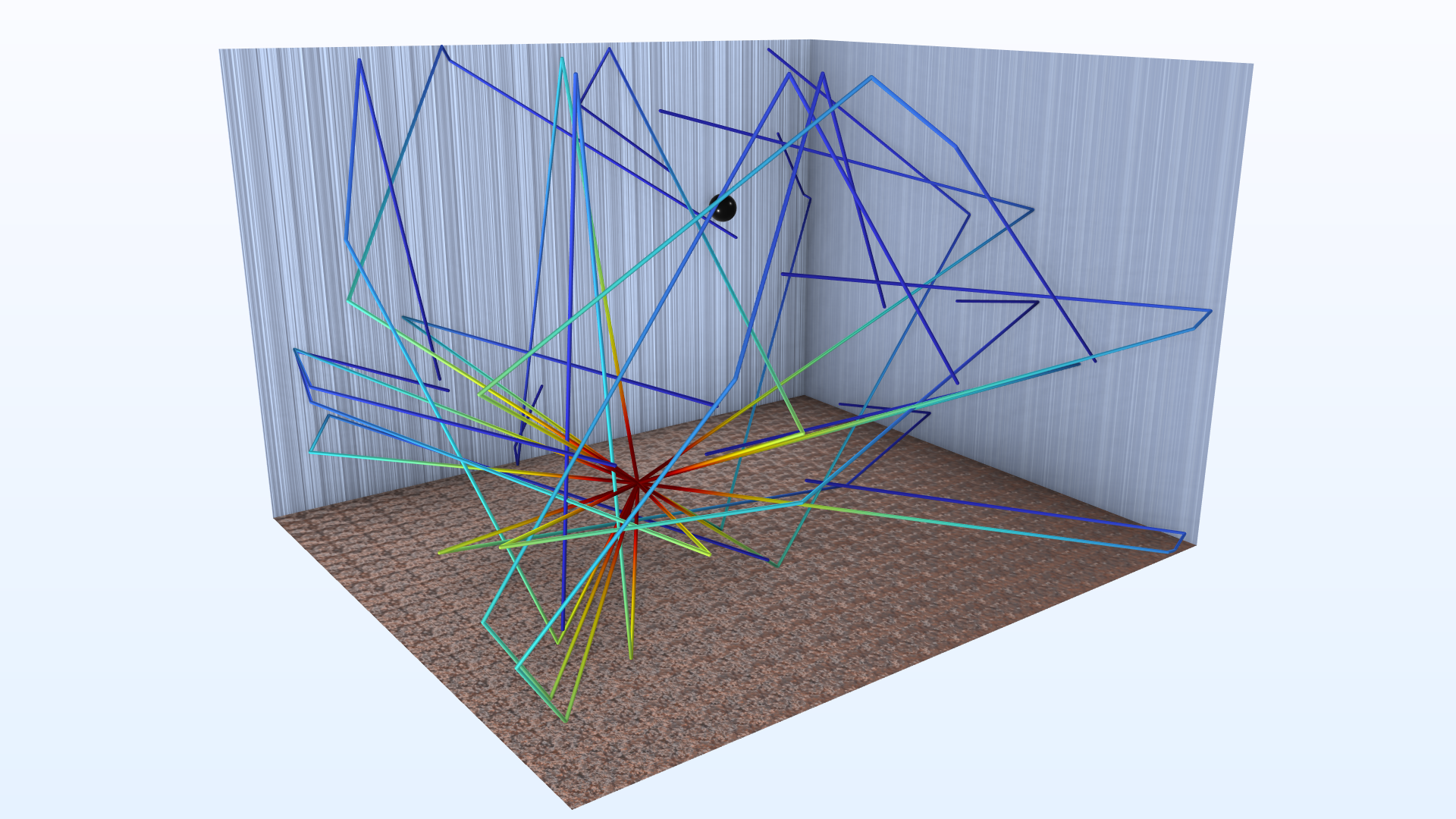
图 10—13 展示了从示例模型中选取的一些结果。图 10 显示了 1000Hz 的压力分布，可以清楚地看到解的波形。在图 11 中，描绘了 1000Hz 频段的射线在同一时刻的位置（对两种方法的不同释放时间进行了修正），比较了点源和压力场描述的释放。从图像中可以清楚地看到，这两种方法给出了不同的空间分辨率（射线密度），因为点源只向上半部空间释放射线，而压力场释放射线也会向下释放射线（由于桌面边缘的衍射）。要对这两种方法进行更正式的比较，应考虑到这一事实。

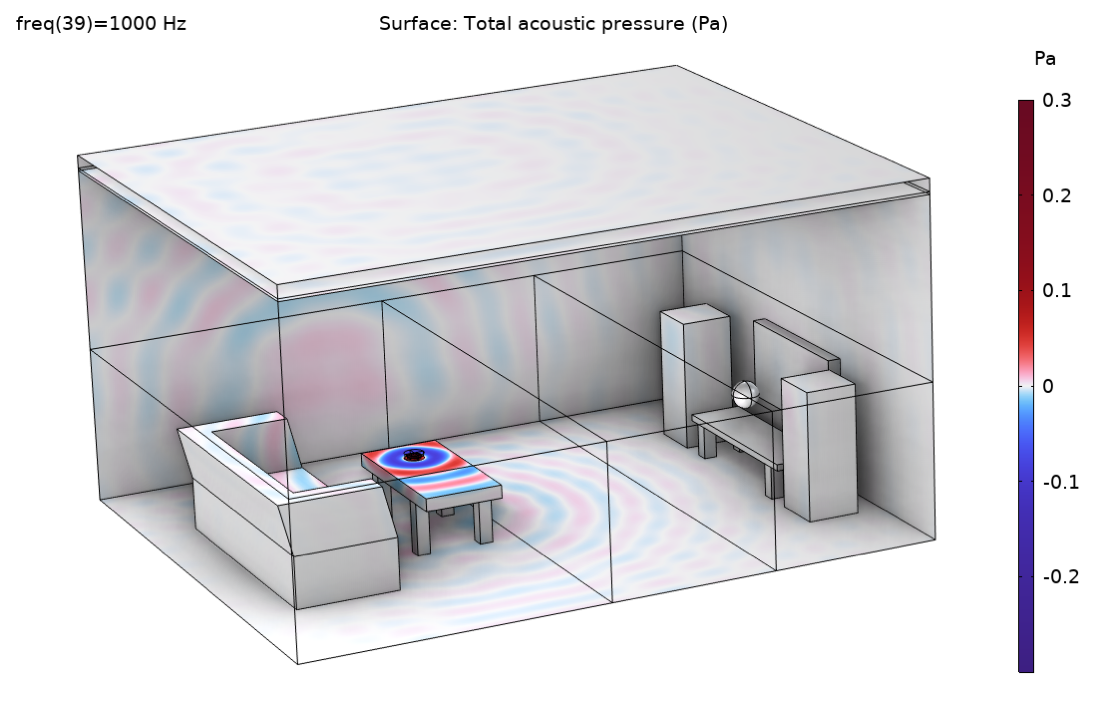
图10. 1000Hz 下的压力分布。

图11. 点声源（左）和压力场释放（右）的射线图。两幅图都显示了在 6ms 时计算的 1k Hz 频带（根据 0 时刻的不同定义进行了近似校正）。请注意色条上不同的射线功率刻度。右图还绘制了声源区域近场的声压。

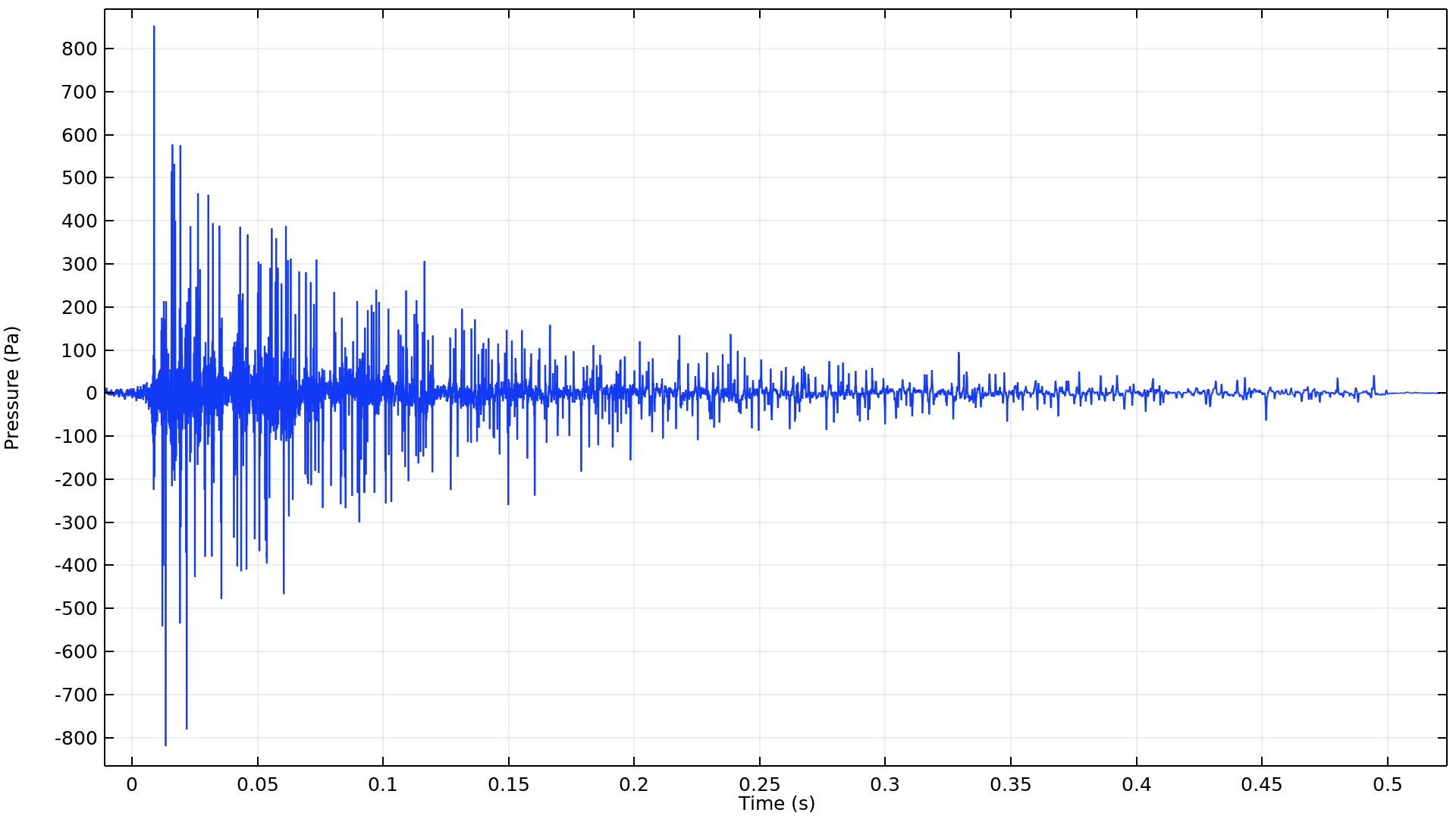
图 12 和图 13 对这两种方法进行了比较。图 12 描述了声源和接收器之间的传递函数。它绘制了两种射线追踪方法和全波有限元模型的脉冲响应（IR）的快速傅立叶变换（FFT）。这里没有对有限元模型结果进行平滑处理，但对射线追踪结果应用了 1/3 倍频程运行平均滤波器处理。该图显示了相同的整体行为，还显示了即使在预期的施罗德频率（垂直线）之上，房间内也有很强的模态行为。两条射线声学结果（蓝色和红色曲线）之间似乎存在更大的水平差异。这可能是因为两种声源描述的能量传播方式不同。最后，图 13 比较了两种射线追踪结果的一些时间特征。我们对早期衰减时间（EDT）和 T20 混响时间进行了比较，从下图中可以看出，两者之间存在显著差异，这表明两种模型到达接收器的能量的时间分布是不同的。

图12. 全波响应和射线声学脉冲响应的快速傅立叶变换。

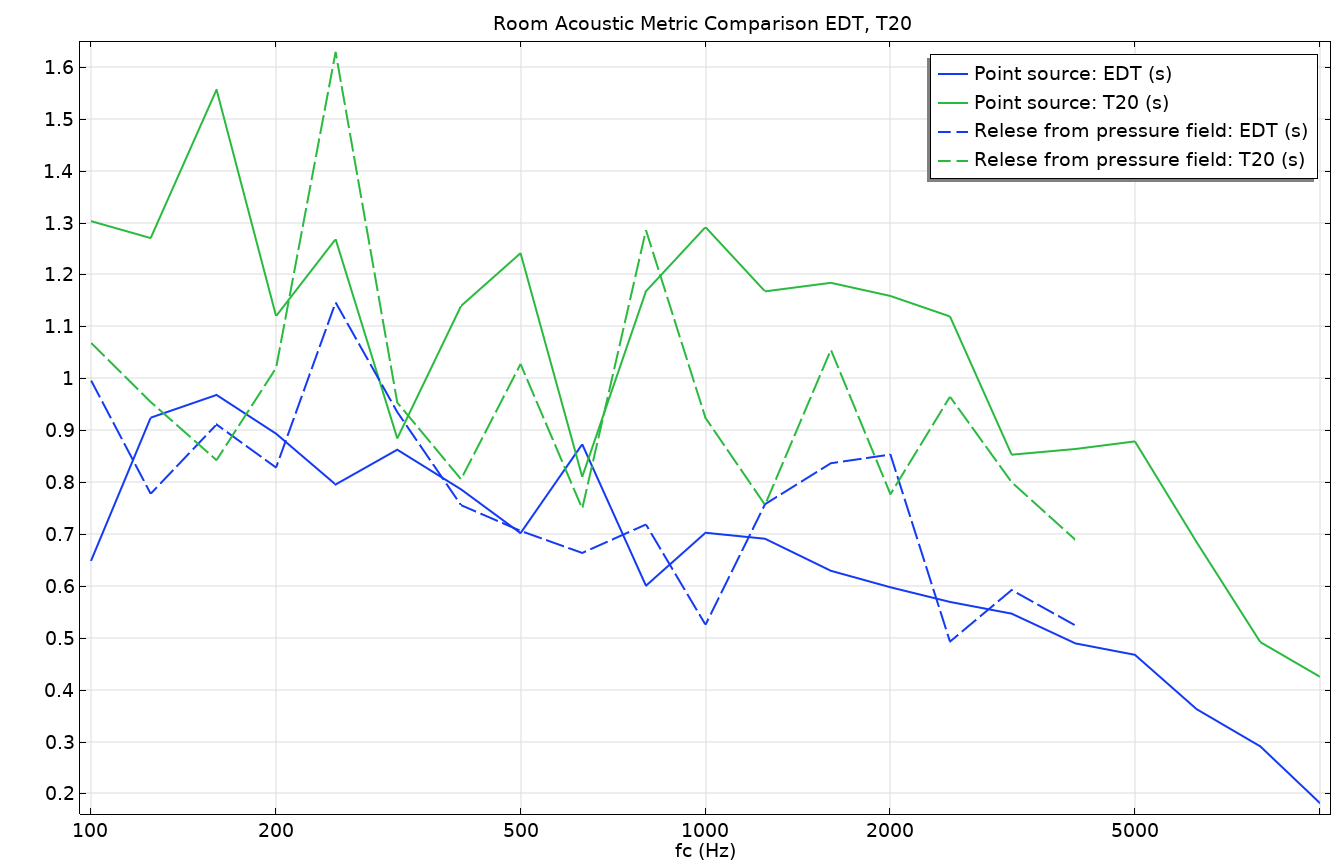
图13. 早期衰减时间和 T20 混响时间的室内声学客观指标比较。

这里讨论的一些结论可以加以完善，用于扩展模型中进行的分析。例如，您可以选择使用更多的射线，比较多个接收器位置，在有限元模型中使用更精细的频率分辨率，或在射线跟踪模型中使用 1/6 倍频程波段。这些不同的选项都可以使用当前模型完成。例如，通过改变参数 Nrays 来改变射线数量，或通过改变参数 xr、yr 和 zr 来改变接收器的位置。

下一步

点击下面的按钮，进入 COMSOL 案例库，进一步探索本博客中讨论的模型。

获取教程模型

其他资源

在 COMSOL 博客上了解有关室内声学建模的更多信息：
- 使用混合方法建立室内声学模型
- 验证室内音乐厅的声学射线追踪仿真
查看相关教程模型：
- 施罗德扩散器二维模型

使用混合方法对室内声学进行建模

Mark Cops — Thu, 23 Feb 2023 02:42:16 +0000

室内声学建模和仿真的一个挑战是准确模拟一个房间内全部频率范围内的声学性能。这篇文章讨论了在 COMSOL Multiphysics^® 软件中对室内声学进行建模的一种混合方法，就是将多种方法的结果集成到一个模型中，来提高准确性并确保方法的可行性。接下来，我们来看看如何做到这一点。

室内声学回顾

在上一篇关于使用 COMSOL Multiphysics 对室内声学进行建模的博客中，我们介绍了 COMSOL 软件的声学模块中可用于建立封闭空间的声学模型的多种方法。文章讨论了:

如何使用压力声学 接口模拟模态行为
如何使用射线声学 接口模拟高频行为
如何使用声学扩散方程 接口模拟高频行为

今天，我们将讨论如何结合使用前两种方法获得一个房间内的宽带脉冲响应。

室内脉冲响应

想象一下，在一个房间里弹起一个充满空气的气球，并在房间的某个位置放置一个麦克风记录与时间相关的声压。麦克风将收到来自第一个波前的直接声音，以及从墙壁、地板、天花板和其他物体上传播和反弹的所有波反射信号的叠加。声音通常会被不同的材料吸收，例如地毯、家具和天花板，最终会完全消失。麦克风记录的声压与时间的关系信号被称为该测量位置的室内脉冲响应。这是一个非常重要的室内声学描述量，因为它可以告诉我们很多关于房间内的声学性能。

左：射线声学模型的结果显示了从声源到麦克风位置的一小部分射线的路径。右：室内脉冲响应示例。

对房间进行建模

对一个房间的声学性能进行建模时，为了确定建模方法的准确性和可行性，仿真工程师必须同时关注声学特性和几何尺度。在 COMSOL 声学模块中，可以使用压力声学,频域 接口通过有限元方法对房间的低频模态行为进行建模。然而，由于网格的要求，这种方法在高频下计算成本很高。我们可以通过射线声学 接口的射线追踪方法对房间的高频混响行为进行建模。虽然这种方法通常计算效率高，但射线追踪不是基于波的方法，不会捕获模态行为。为了准确模拟房间的脉冲响应，两种模型都可以在各自的频率范围内运行，并可以结合使用两种方法来获得全部频率范围内的响应。

考虑一个 4.7m x 4.1m x 3.1m 的矩形房间。本例中所有的壁都使用与频率相关的吸收系数进行建模。该模型的目标是确定位于坐标（3，3，2）m 处的麦克风的脉冲响应。事实证明，对于一个考虑“轻微”吸收壁的单极脉冲源，房间内任何一点的压力都有三维解析解。遵循参考文献1和参考文献2中的符号标记，任何一点的压力都可以用格林函数来表示，格林函数由在接收器和源位置计算的无阻尼房间模式形状和一个与频率相关的阻尼项构成。表达式为：

P(r) = i \rho_0 \omega Q G(r,r_0)

G(r,r_0) = \sum_{mnp} \frac{\psi_{mnp}(r)\psi_{mnp}(r_0)}{V \Lambda_{mnp}(k^2_{mnp}-k^2 -i \tau_{mnp})}

式中，是密度，是频率，是单极域源体积速度。格林函数表示三个正交笛卡尔方向上模态的三次求和，指数表示不同的模态。s 表示模态形状，是模态的余弦函数乘积，是体积空间的模态整数因子。波数为。关于分析解的完整说明，请查阅参考文献1和参考文献2。对于这个建模方案，定义解析解的变量已经添加到组件1 定义变量1-解析解 中。

就像我们之前的博客中所讨论的，模态和混响房间行为之间没有明确的过渡频率，但可以根据Schroeder提出的标准（参考文献 3，4）进行估计。在这个案例中，Schroeder 频率接近 370Hz，并通过全局定义 射线参数计算。上面的解析解将作为参考解与数值模型进行比较。

压力声学

理想情况下，我们可能希望在全部频率范围内使用基于波的方法对房间内的声学性能进行建模，但由于网格要求，这在高频下不可行。我们知道低于 Schroeder 频率的单个模态的贡献占室内响应主导地位，因此选择使用略高于 Schroeder 频率的最大频率求解压力声学：在这个案例中，频率高达 500Hz。压力声学模型的设置包括：

含压力声学、频域 接口的 3D 组件
含恒定功率的单极点源
指定壁面的频率相关阻抗条件（吸收系数）
能解析空气中 500Hz 以下的波长的体网格
频域研究

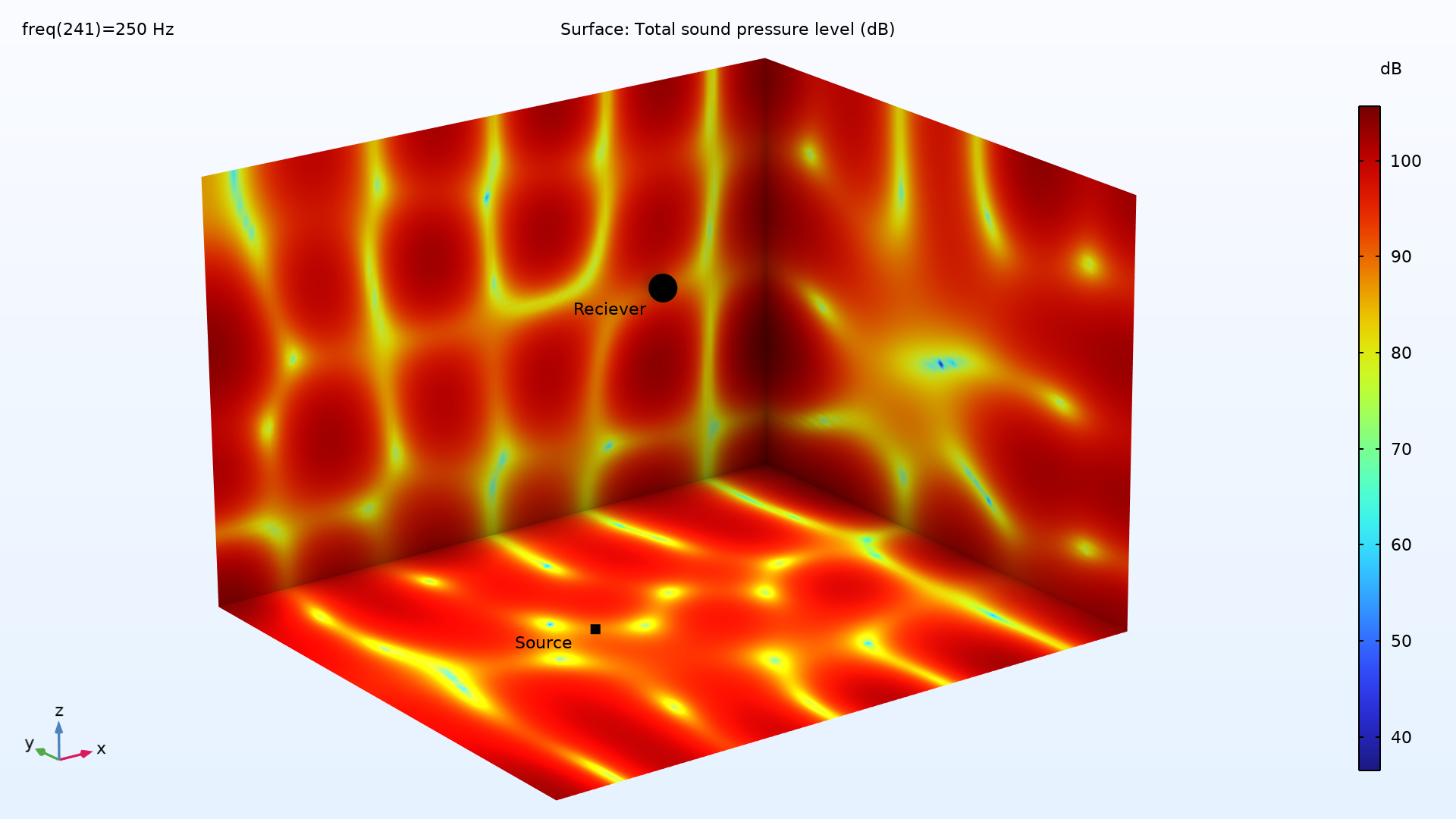
矩形房间三面壁上的声压级（分贝的参考值为 20μPa），频率为 250Hz。

上图示例显示了房间壁上的总声压级分布。使用这种方法，我们已经模拟了房间内声学的低频行为（低于 500Hz）。为了模拟房间内声学的高频行为，我们将切换到射线声学。

射线声学

射线声学模型设置如下：

使用射线声学 接口添加 3D 组件
使用频率相关吸收系数指定壁面条件
使用从栅格释放 条件，按照指定功率从源点释放 8000 条射线
如果功率水平低于阈值，使用射线终止 标准停止追踪射线，从而降低自由度
使用高达 4000kHz 的超过 1/3 倍频程带频率的参数扫描进行射线追踪研究

下图显示了从点光源释放出射线时的屏幕截图。请注意，为了可视化图像，下面仅显示了一小部分光线。（y 坐标上小于源位置的射线被隐藏。）

3 ms 时的射线轨迹显示了从单极点源释放的射线。色阶代表射线压力，单位为 Pa。

射线追踪研究不是以精细步长运行的。那么脉冲响应如何计算的呢？在 COMSOL Multiphysics 中，有一个专用的 接收器 数据集和一维脉冲响应 绘图可用于此计算。该绘图组采用 1/3 倍频程输入，例如射线功率、频率、反射次数和流体特性，并重构频率范围内的脉冲响应。目标是获得一个新信号，当对输入的倍频程频段进行平均时，该信号的能量含量与真实信号相同。这是通过将脉冲信号与选定的红外滤光核（默认是带有 Kaiser 窗口的砖壁）进行卷积，然后将所有频段上所有射线的贡献进行汇总来完成的。有关重构的更多信息，请查看声学模块用户指南。

下图显示了麦克风位置处的声压级。由于单极点源代表一个时间上的脉冲，因此房间的脉冲响应也可以在频域中解释，其中源是频率范围内的一个宽带激励。（狄拉克 δ 函数在时间上的傅里叶变换是一个与频率有关的恒定函数。）

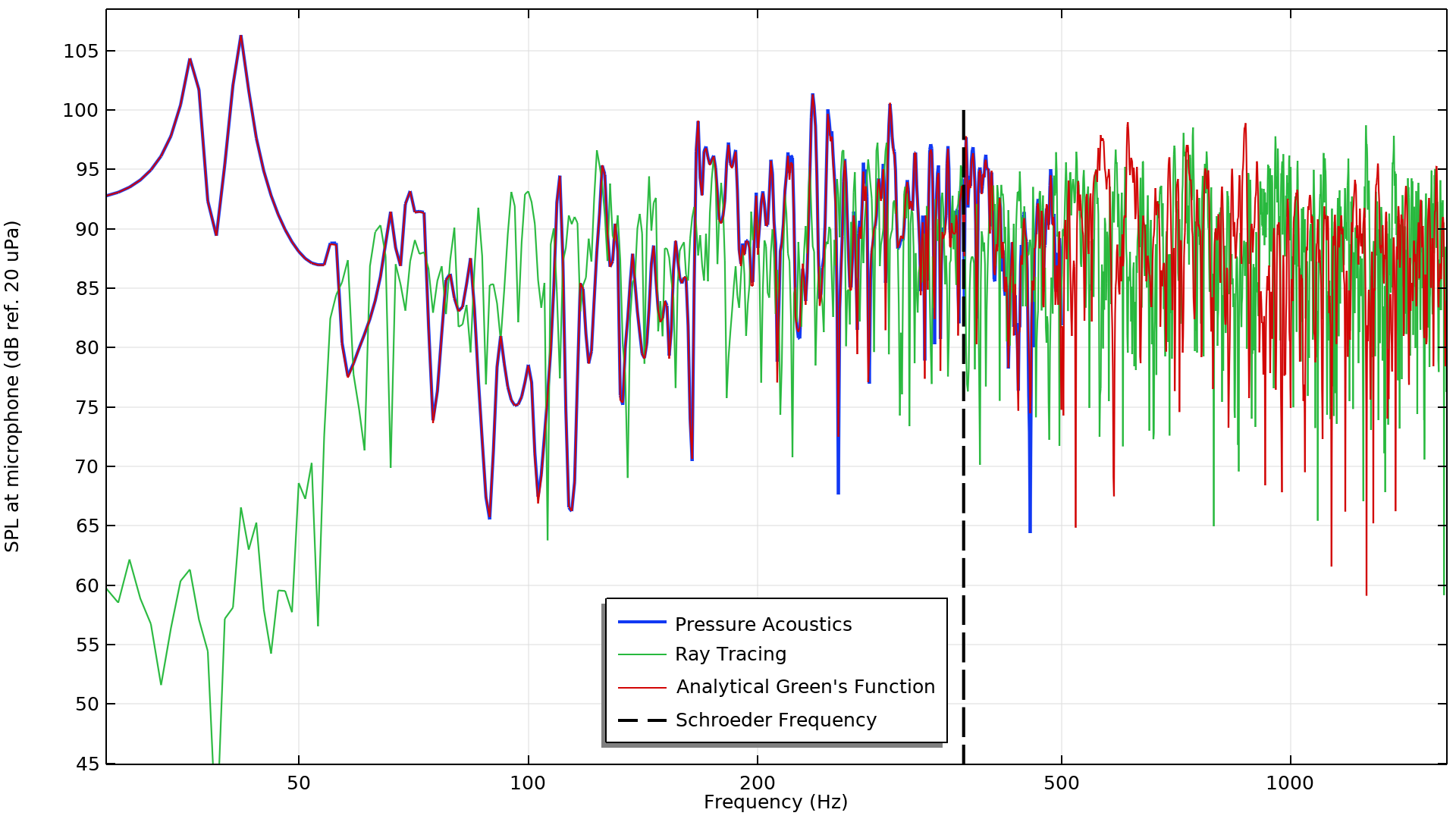
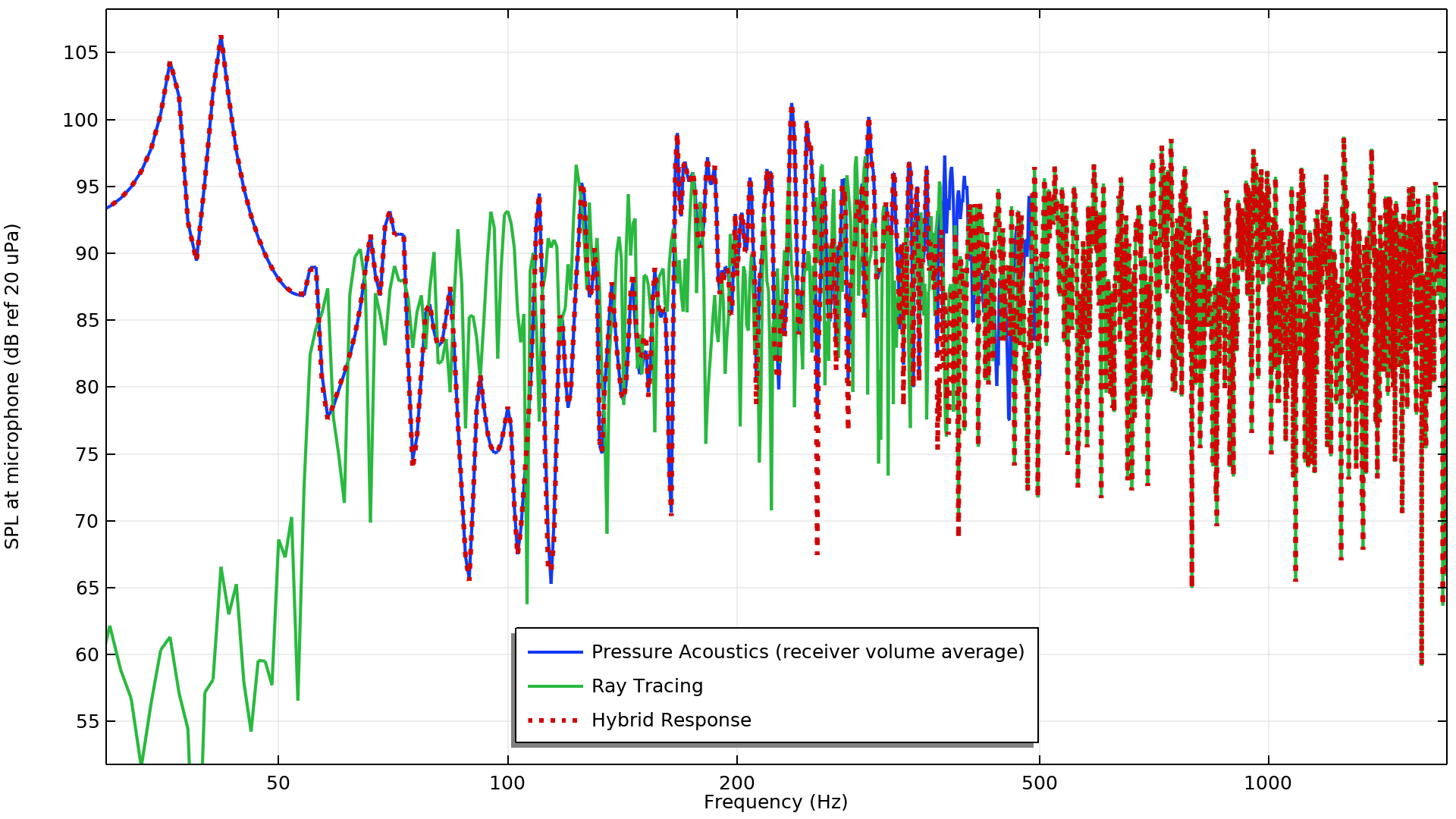
通过压力声学研究、射线追踪研究和解析的公式计算的麦克风声压级。黑色虚线表示施罗德频率。

根据这个图，我们可以得出几个关键的结论。首先，分析结果与高达 500Hz 的压力声学研究结果非常吻合，这是该研究中的最大频率。这个结果可以作为一个良好的基准，表明模型的设置是正确的。

将射线追踪结果与其他结果进行比较时，很明显低频声压级并不匹配。这些结果是意料之中的，因为射线追踪本质上不是一种基于波的方法，并且不能捕获在低频下占主导地位的模态行为。我们可以得出结论，射线追踪结果在低频下并不准确，尤其是在这个模型中当频率低于 50Hz 时。

压力声学图中的前两个共振峰对应于两种不同的模态，它们被脉冲源激发，但声能还没有被壁强烈吸收。由于我们在模型中考虑了弱吸收，因此这里的模态几乎等于具有硬声场壁的房间的模态。参考文献5推导并计算了考虑刚性边界条件的相同大小房间（4 .7m x 4.1m x 3.1m）的前 20 种模态（参见参考文献5中的表3.1）。前两种模式是 36.17Hz 的（1，0，0）模态和 41.46Hz 的（0，1，0）模态。它们分别对应于 x 方向和 y 方向上的第一种模态，并与上图中的前两个峰值保持一致。

117Hz 以下有 20 种模式，随着频率的增加，越来越多的模态会影响房间的混响行为。在低频下，模态间隔很远，并且模态的带宽也不重叠。在高频下，模态确实会重叠，这会导致嘈杂的频率响应。由于射线追踪不是一种基于波的方法，因此即使高于施罗德频率，射线追踪的结果也不会与解析结果完全一致。然而，射线追踪和解析结果都显示出与施罗德频率以上的声压级相似的特征和范围。这意味着，高于施罗德频率的射线追踪结果可用于准确估计脉冲响应，其标准是根据在输入倍频程频段上取平均值时，保持与真实信号相同的能量含量。

组合方法

我们还可以将压力声学和射线声学模型的结果组合在一起，创建宽带脉冲响应信号。与参考文献6中描述的方法类似，这可以通过采用低通滤波压力声学响应，并将其添加到高通滤波射线声学响应中来完成。这个方法利用了傅里叶变换的线性特性。

使用的滤波器类型和信号过滤位置的名称不是由任何工程标准设定的。可以根据行业具体实践或工程判断选择所实施的数字信号处理技术。这个模型通过简单的理想阶跃滤波器过滤施罗德频率以下的信号，演示了组合的概念。

信号组合的设置如下:

用全局常微分方程和微分代数方程 接口的零维组件
将射线声学 模型的结果导出到文件中，并作为插值曲线导入组件3
使用研究设置中的因变量值 将压力声学 模型的结果传递到研究3

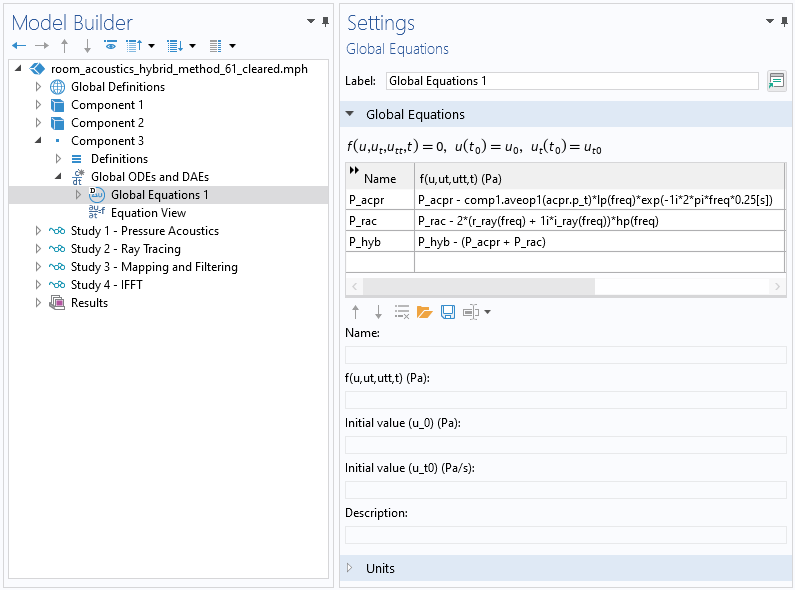
在下图中，全局方程 被添加到了组件3:

添加到 组件3 的全局方程。

这里，P_acpr 是接收器处的体积平均压力。该表达式显示了压力经过低通滤波并随时间偏移（0.25s），以符合脉冲响应 绘图类型的惯例，方便后续进行比较。P_rac 是来自脉冲响应快速傅里叶变换（FFT）的插值函数的压力。表达式 P_rac 使用了插值函数 r_ray 和 i_ray ，即射线追踪研究（研究2）的压力的实部和虚部。通过压力表达式还可以看出射线压力通过了高通滤波并乘 2。系数为 2 是因为在研究3中仅计算了正频率，而插值是针对全频谱的。最后， P_hyb 是低通滤波压力声学响应和高通滤波射线追踪响应的总和（使用的方法与参考文献6中使用的方法类似）。

下图显示了原始信号和仅使用 组件3运行频域研究后组合信号的比较。在这幅图中，我们可以看到，压力声学和射线追踪结果的结合使混合响应具有正确的频率响应。

通过压力声学、射线追踪和混合方法计算的麦克风声压级。

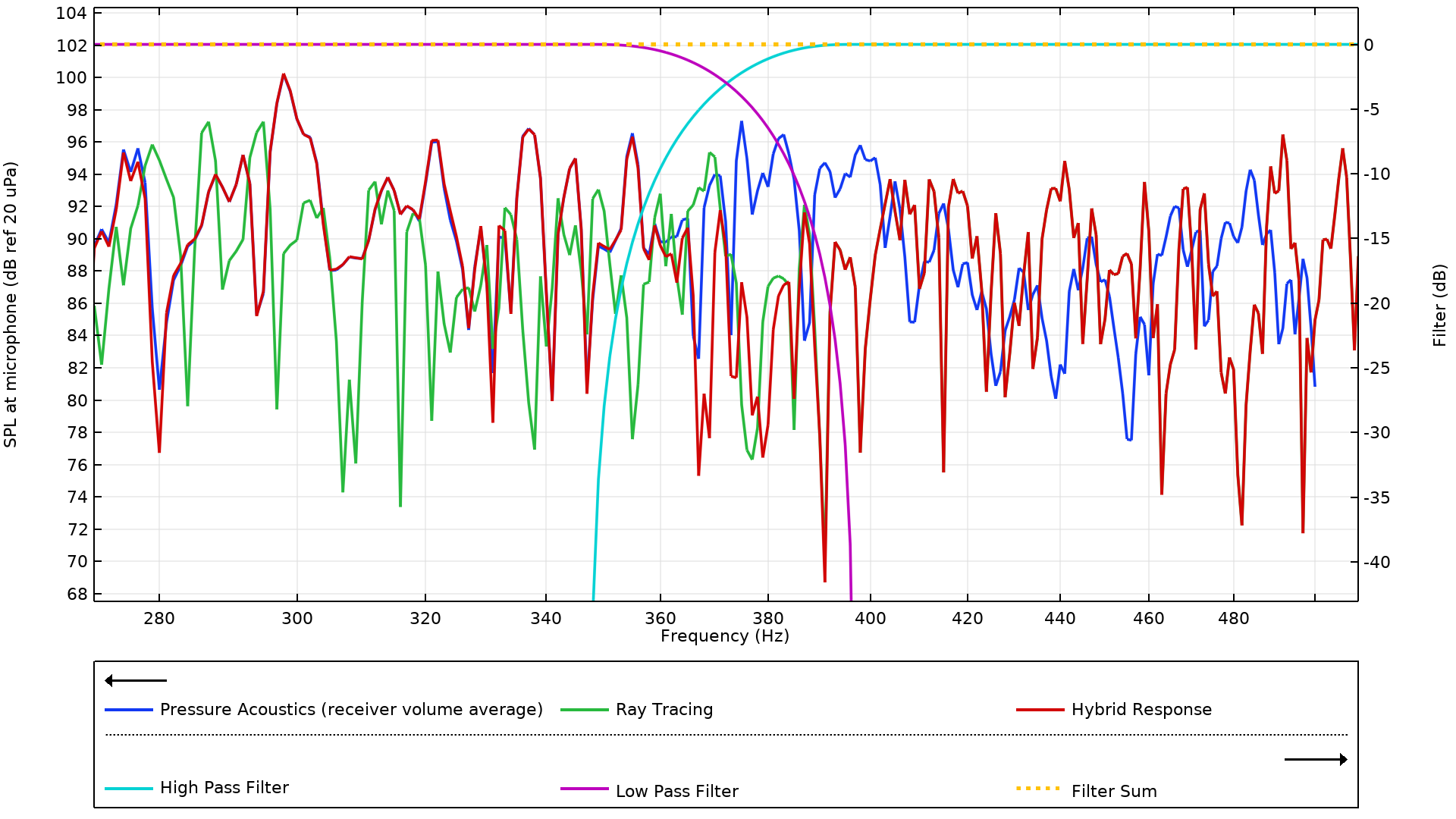
理想的滤波器是使用阶跃函数实现的，对于高通滤波器 hp(freq)，从 0 步进到 1，对于低通滤波器 lp(freq)，从 1 步进到 0。两个功能中都包含一个 50Hz 平滑过渡区，并将阶跃转换的位置设置为施罗德频率。将两个函数都添加到组件3 定义下。下图显示了施罗德频率附近的混合响应。从图中我们可以分析理想滤波器的特性。值得注意的是，理想滤波器在施罗德频率下的增益因数均为 -3dB，这意味着这里的响应是两者的平均值。在其他地方，混合响应是两种响应的加权组合，具体取决于频率。滤波器的总和在所有频率上都是 0dB。

接近施罗德频率的滤波器平均混合压力。

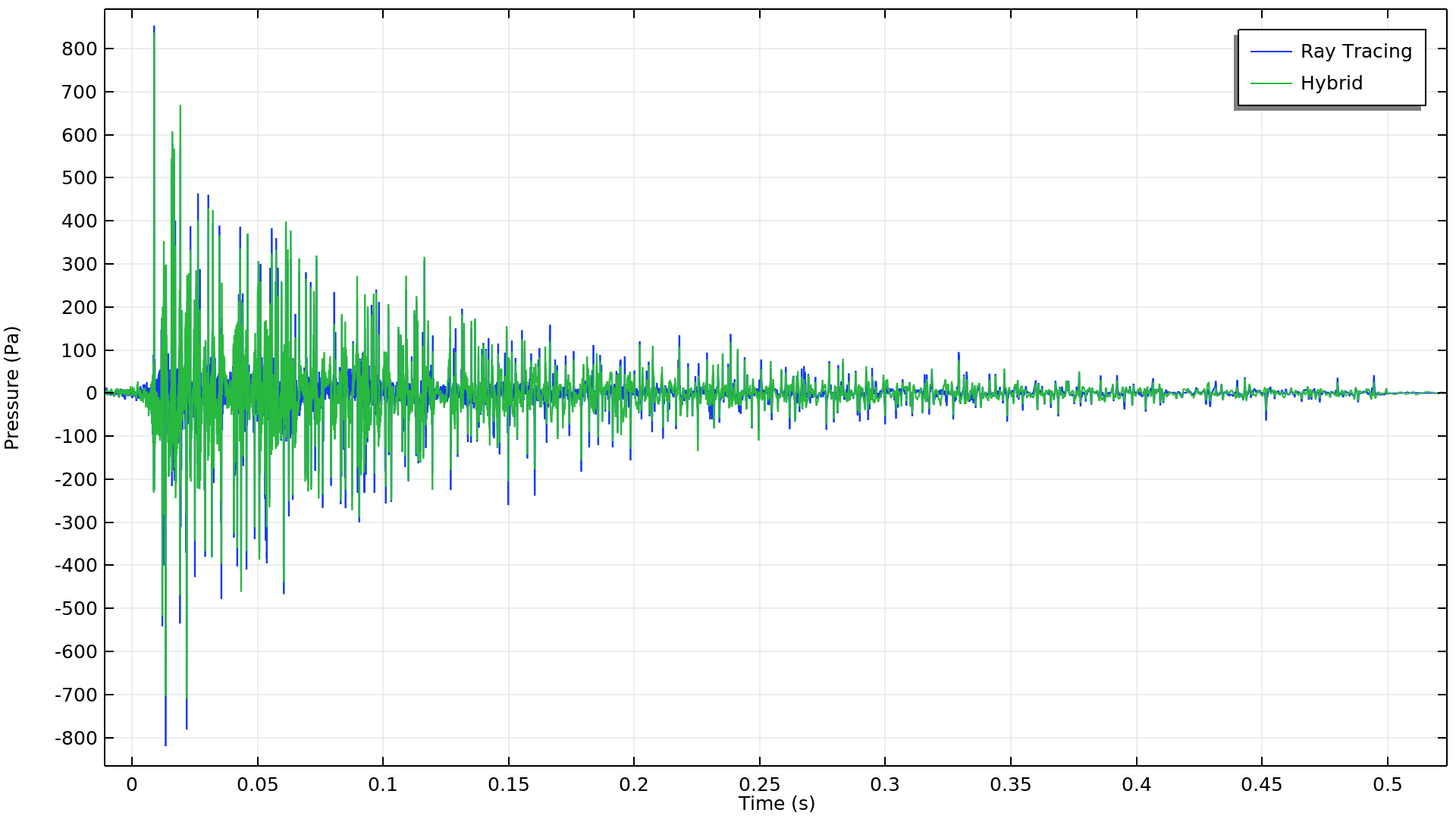
为了从频率分析返回时域分析，我们运行第四个也是最后一个研究，包括一个从频域时间域的 FFT 步骤。在这个步骤中，Tukey 窗口函数用于对逆 FFT（IFFT）进行带限制。混合信号和原始射线追踪信号的比较如下图所示。虽然我们在时域中可以看到一些差异，但通过直接查看频谱更容易发现差异。很明显，在全部频率范围内，这里计算的混合压力与时间信号比纯射线追踪信号更准确。这种精度意味着混合信号可用于计算其他室内声学指标，例如清晰度、混响时间或语音传输指数，或导出用于房间听觉化的外部分析工具。

使用射线追踪和混合方法得到的压力与时间脉冲响应的比较。

动手尝试

这篇文章，我们介绍了一种将射线追踪和有限元方法组合使用来获得宽带脉冲响应的方法。文中显示的所有模拟都是在 COMSOL Multiphysics 中完成的，并且解被集成到单个模型中。这个方法对于在高频下使用全波方法可能并不总是可行，但对于大型室内声学仿真特别有用。单击下面的按钮，尝试自己动手，您可以从 COMSOL 案例库中下载该模型文件：

试用教程模型

参考文献

Morse, Philip McCord, and K. Uno Ingard. Theoretical Acoustics. Princeton University Press, 1986.
Okoyenta, Augustus R., et al. “A Short Survey on Green’s Function for Acoustic Problems.” Journal of Theoretical and Computational Acoustics 28.02 (2020): 1950025.
M. R. Schroeder, New Method of Measuring Reverberation Time, J. Acoust. Soc. Am., 37 (1965).
M. R. Schroeder, Integrated-Impulse method measuring sound decay without using impulses, J. Acoust. Soc. Am., 66 (1979).
Kuttruff, Heinrich. Room Acoustics. CRC Press, 2016.
Aretz, Marc, et al. “Combined broadband impulse responses using FEM and hybrid ray-based methods.” EAA Symposium on Auralization, 2009.