论文和技术资料

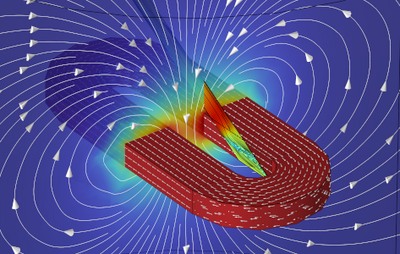
Superconducting coils are used to generate high magnetic fields in various applications such as nuclear fusion reactors, particle accelerators, actuators and MRI scanners. Electrodynamic modelling of superconductors is challenging because of the significant nonlinearity in the electric field–current (E(J)) relation. In contrast to regular conductors, where the electric field and current are linearly dependent variables (i.e. Ohm’s law), the superconductor E(J) curve is E(J) = EC (J/JC)^n with n ~ 20. The conventional method for modelling superconductors involves specialized formulations. The most prominent and simple is the H-formulation, where the magnetic H-field is the dependent variable and the current is given by its curl, as follows from Ampère’s law. The downside of the conventional superconductor modelling formulations is that the voltage is usually not readily available in the simulations and if it is, it is only in lumped form. We have modified the AV-formulation to get the best of both worlds: spatially resolved voltages as well as the correct E(J) curve.

Here, we studied the case of a single superconducting coil and the influence of its magnetic fi-eld on the current distribution and critical current in the superconducting tape that is feeding it (the lead). We simultaneously calculate the magnetic fi¬eld, the electrical current and the voltage inside the superconductor.

The AV-formulation allows us direct access to the voltage drop over the superconducting lead. The current inside the coil is as an external current density that generates a magnetic field; its superconducting properties are not relevant and not directly modeled. The lead and coil are connected by a soldered interface which is taken into account in the simulation. This is necessarily a metallic (non-superconducting) interface, which introduces an Ohmic term into the voltage drop over the entire lead. As there is access to the spatially resolved voltage (thanks to the modified AV-formalism), it is possible to obtain the voltage drop over the superconducting tape only. The end result is that we have unambiguous, reliable numerical results for the voltage drop over the superconducting lead as a function of the applied current. This directly allows us to find the effective critical current (defined to be the current value at which the critical E-field at 1·10-4 V/m is reached) of the entire lead.